Scalable Backdoor Detection in Neural Networks

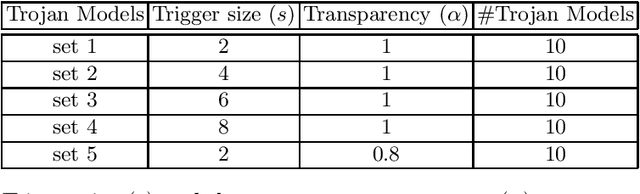
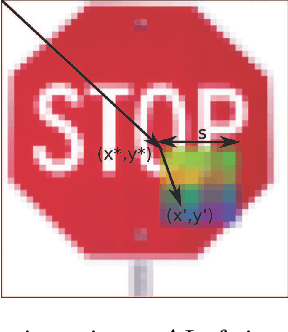
Recently, it has been shown that deep learning models are vulnerable to Trojan attacks, where an attacker can install a backdoor during training time to make the resultant model misidentify samples contaminated with a small trigger patch. Current backdoor detection methods fail to achieve good detection performance and are computationally expensive. In this paper, we propose a novel trigger reverse-engineering based approach whose computational complexity does not scale with the number of labels, and is based on a measure that is both interpretable and universal across different network and patch types. In experiments, we observe that our method achieves a perfect score in separating Trojaned models from pure models, which is an improvement over the current state-of-the art method.

Randomised Gaussian Process Upper Confidence Bound for Bayesian Optimisation

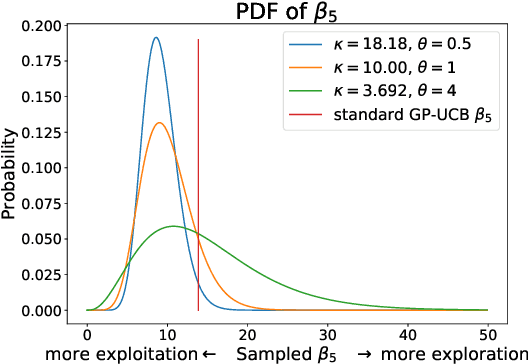
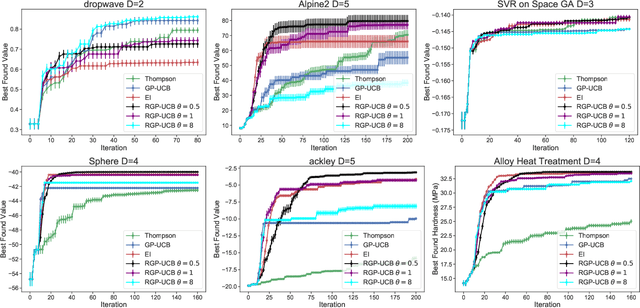
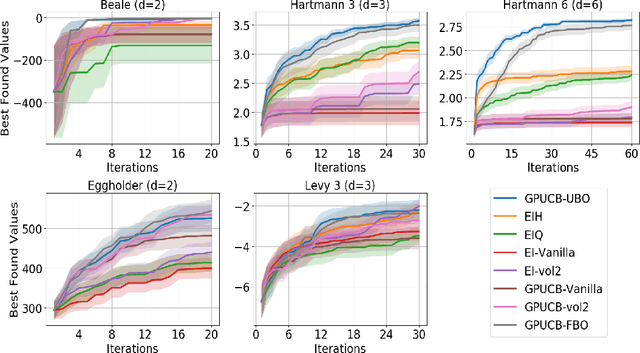
In order to improve the performance of Bayesian optimisation, we develop a modified Gaussian process upper confidence bound (GP-UCB) acquisition function. This is done by sampling the exploration-exploitation trade-off parameter from a distribution. We prove that this allows the expected trade-off parameter to be altered to better suit the problem without compromising a bound on the function's Bayesian regret. We also provide results showing that our method achieves better performance than GP-UCB in a range of real-world and synthetic problems.

HyperVAE: A Minimum Description Length Variational Hyper-Encoding Network

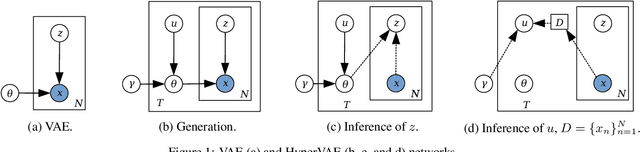
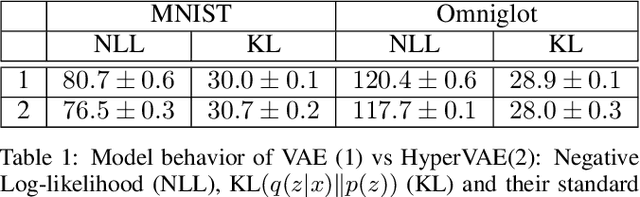
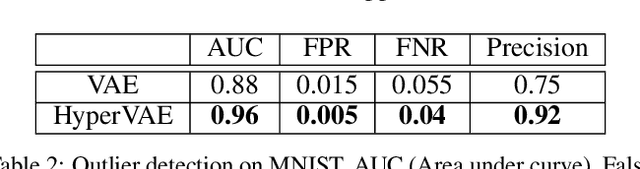
We propose a framework called HyperVAE for encoding distributions of distributions. When a target distribution is modeled by a VAE, its neural network parameters \theta is drawn from a distribution p(\theta) which is modeled by a hyper-level VAE. We propose a variational inference using Gaussian mixture models to implicitly encode the parameters \theta into a low dimensional Gaussian distribution. Given a target distribution, we predict the posterior distribution of the latent code, then use a matrix-network decoder to generate a posterior distribution q(\theta). HyperVAE can encode the parameters \theta in full in contrast to common hyper-networks practices, which generate only the scale and bias vectors as target-network parameters. Thus HyperVAE preserves much more information about the model for each task in the latent space. We discuss HyperVAE using the minimum description length (MDL) principle and show that it helps HyperVAE to generalize. We evaluate HyperVAE in density estimation tasks, outlier detection and discovery of novel design classes, demonstrating its efficacy.

Incorporating Expert Prior in Bayesian Optimisation via Space Warping

Bayesian optimisation is a well-known sample-efficient method for the optimisation of expensive black-box functions. However when dealing with big search spaces the algorithm goes through several low function value regions before reaching the optimum of the function. Since the function evaluations are expensive in terms of both money and time, it may be desirable to alleviate this problem. One approach to subside this cold start phase is to use prior knowledge that can accelerate the optimisation. In its standard form, Bayesian optimisation assumes the likelihood of any point in the search space being the optimum is equal. Therefore any prior knowledge that can provide information about the optimum of the function would elevate the optimisation performance. In this paper, we represent the prior knowledge about the function optimum through a prior distribution. The prior distribution is then used to warp the search space in such a way that space gets expanded around the high probability region of function optimum and shrinks around low probability region of optimum. We incorporate this prior directly in function model (Gaussian process), by redefining the kernel matrix, which allows this method to work with any acquisition function, i.e. acquisition agnostic approach. We show the superiority of our method over standard Bayesian optimisation method through optimisation of several benchmark functions and hyperparameter tuning of two algorithms: Support Vector Machine (SVM) and Random forest.

Incorporating Expert Prior Knowledge into Experimental Design via Posterior Sampling

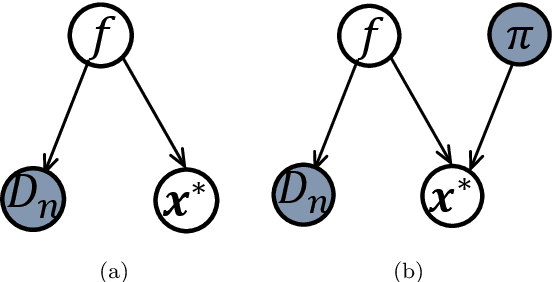
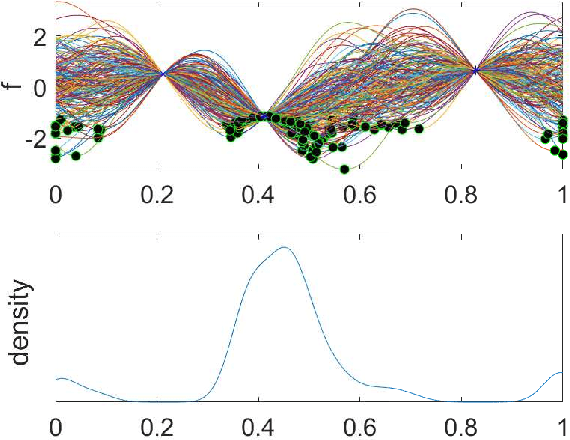
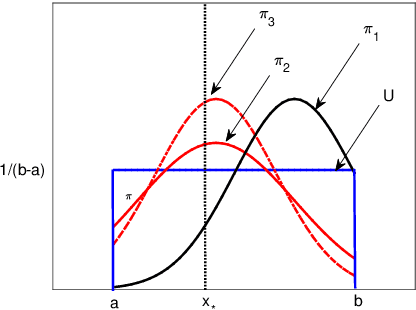
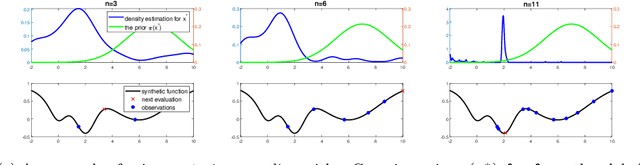
Scientific experiments are usually expensive due to complex experimental preparation and processing. Experimental design is therefore involved with the task of finding the optimal experimental input that results in the desirable output by using as few experiments as possible. Experimenters can often acquire the knowledge about the location of the global optimum. However, they do not know how to exploit this knowledge to accelerate experimental design. In this paper, we adopt the technique of Bayesian optimization for experimental design since Bayesian optimization has established itself as an efficient tool for optimizing expensive black-box functions. Again, it is unknown how to incorporate the expert prior knowledge about the global optimum into Bayesian optimization process. To address it, we represent the expert knowledge about the global optimum via placing a prior distribution on it and we then derive its posterior distribution. An efficient Bayesian optimization approach has been proposed via posterior sampling on the posterior distribution of the global optimum. We theoretically analyze the convergence of the proposed algorithm and discuss the robustness of incorporating expert prior. We evaluate the efficiency of our algorithm by optimizing synthetic functions and tuning hyperparameters of classifiers along with a real-world experiment on the synthesis of short polymer fiber. The results clearly demonstrate the advantages of our proposed method.

Distributionally Robust Bayesian Quadrature Optimization

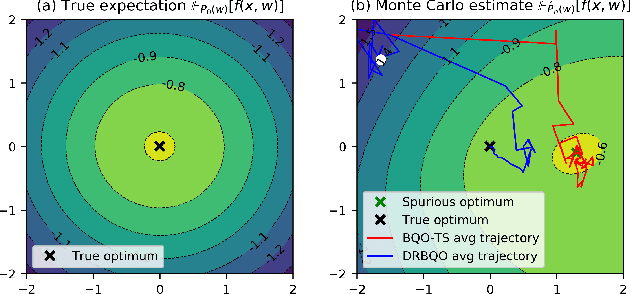
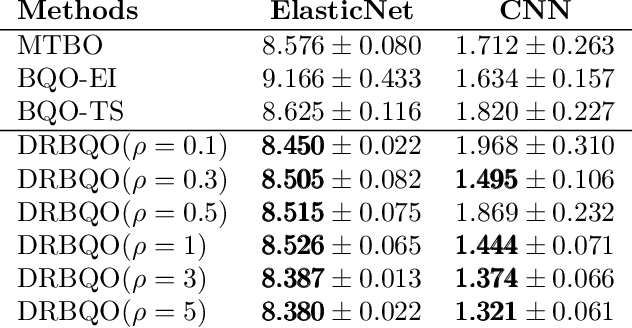
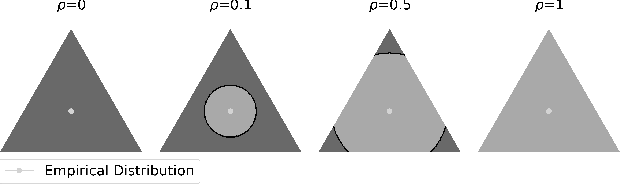
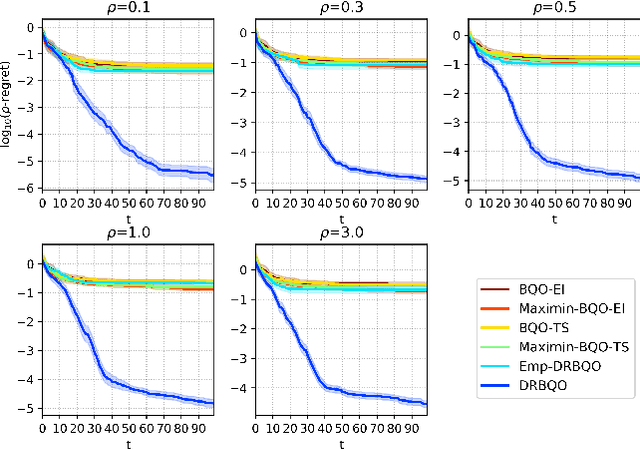
Bayesian quadrature optimization (BQO) maximizes the expectation of an expensive black-box integrand taken over a known probability distribution. In this work, we study BQO under distributional uncertainty in which the underlying probability distribution is unknown except for a limited set of its i.i.d. samples. A standard BQO approach maximizes the Monte Carlo estimate of the true expected objective given the fixed sample set. Though Monte Carlo estimate is unbiased, it has high variance given a small set of samples; thus can result in a spurious objective function. We adopt the distributionally robust optimization perspective to this problem by maximizing the expected objective under the most adversarial distribution. In particular, we propose a novel posterior sampling based algorithm, namely distributionally robust BQO (DRBQO) for this purpose. We demonstrate the empirical effectiveness of our proposed framework in synthetic and real-world problems, and characterize its theoretical convergence via Bayesian regret.

Bayesian Optimization for Categorical and Category-Specific Continuous Inputs

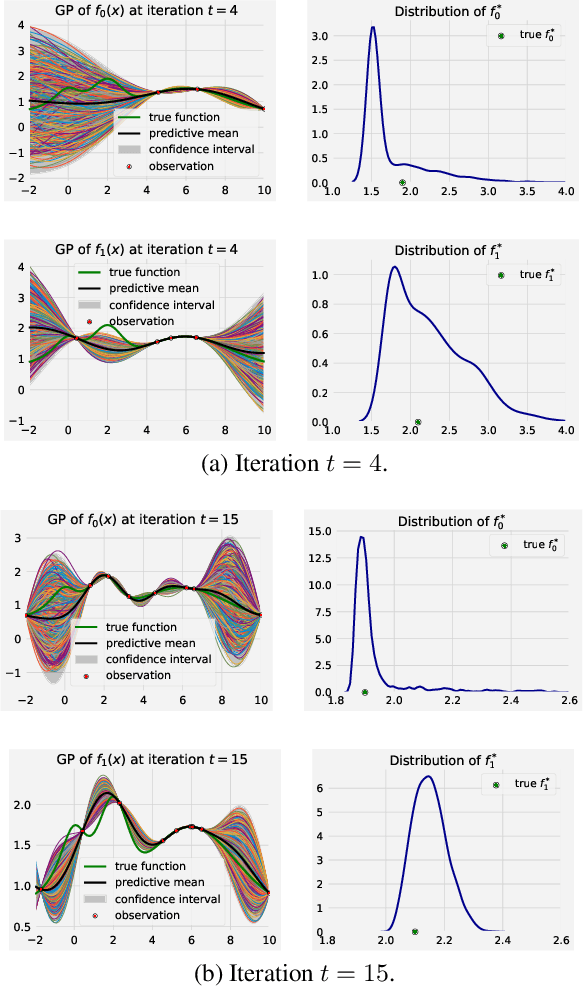
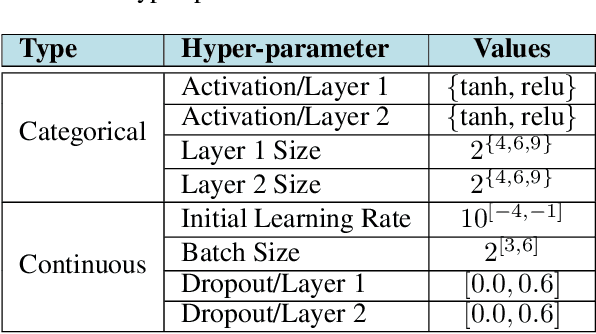
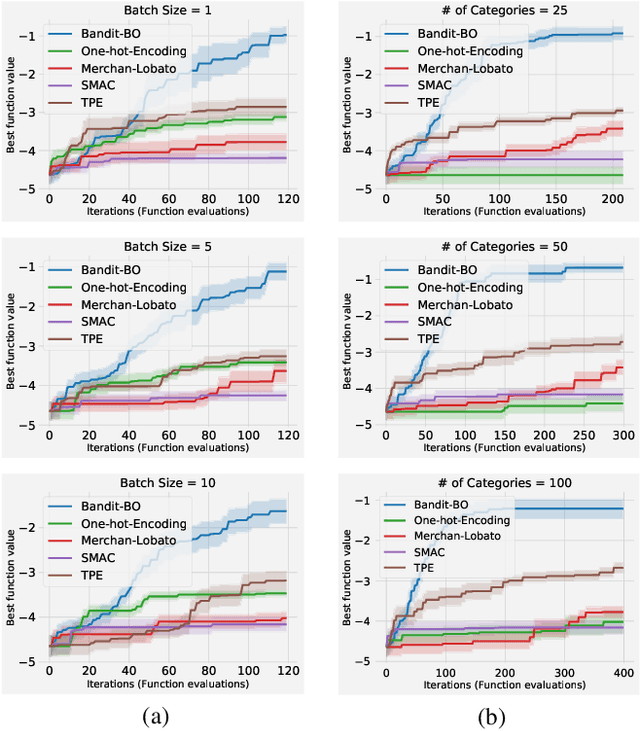
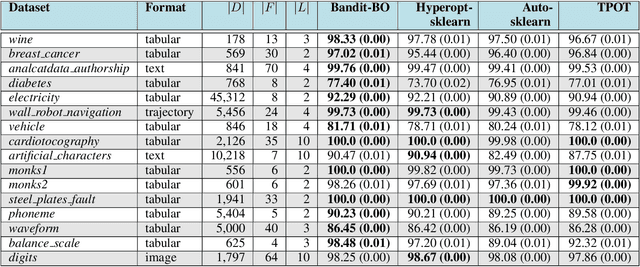
Many real-world functions are defined over both categorical and category-specific continuous variables and thus cannot be optimized by traditional Bayesian optimization (BO) methods. To optimize such functions, we propose a new method that formulates the problem as a multi-armed bandit problem, wherein each category corresponds to an arm with its reward distribution centered around the optimum of the objective function in continuous variables. Our goal is to identify the best arm and the maximizer of the corresponding continuous function simultaneously. Our algorithm uses a Thompson sampling scheme that helps connecting both multi-arm bandit and BO in a unified framework. We extend our method to batch BO to allow parallel optimization when multiple resources are available. We theoretically analyze our method for convergence and prove sub-linear regret bounds. We perform a variety of experiments: optimization of several benchmark functions, hyper-parameter tuning of a neural network, and automatic selection of the best machine learning model along with its optimal hyper-parameters (a.k.a automated machine learning). Comparisons with other methods demonstrate the effectiveness of our proposed method.

Trading Convergence Rate with Computational Budget in High Dimensional Bayesian Optimization

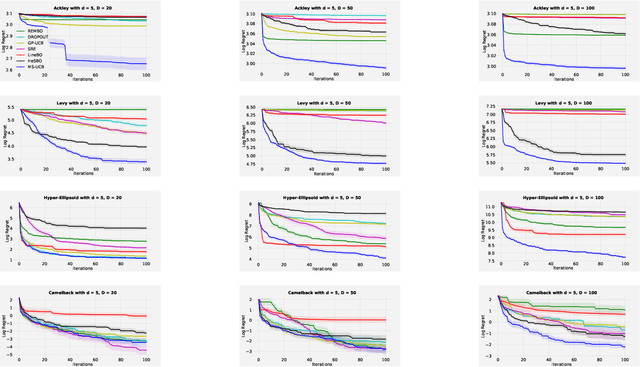
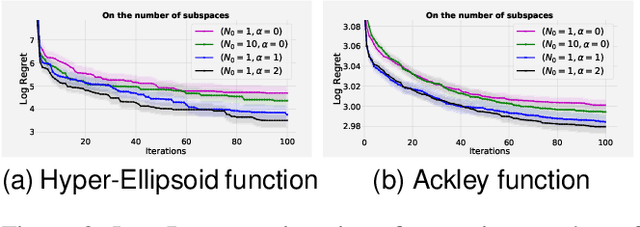
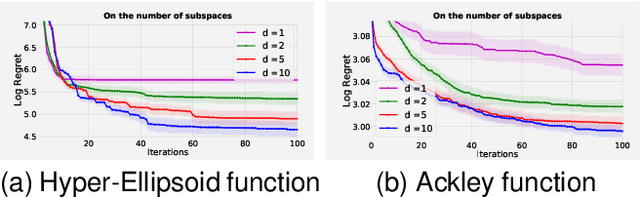
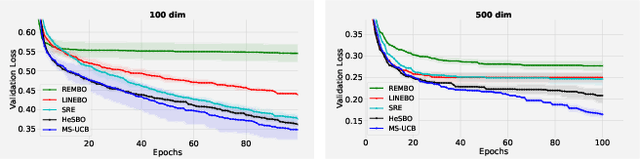
Scaling Bayesian optimisation (BO) to high-dimensional search spaces is a active and open research problems particularly when no assumptions are made on function structure. The main reason is that at each iteration, BO requires to find global maximisation of acquisition function, which itself is a non-convex optimization problem in the original search space. With growing dimensions, the computational budget for this maximisation gets increasingly short leading to inaccurate solution of the maximisation. This inaccuracy adversely affects both the convergence and the efficiency of BO. We propose a novel approach where the acquisition function only requires maximisation on a discrete set of low dimensional subspaces embedded in the original high-dimensional search space. Our method is free of any low dimensional structure assumption on the function unlike many recent high-dimensional BO methods. Optimising acquisition function in low dimensional subspaces allows our method to obtain accurate solutions within limited computational budget. We show that in spite of this convenience, our algorithm remains convergent. In particular, cumulative regret of our algorithm only grows sub-linearly with the number of iterations. More importantly, as evident from our regret bounds, our algorithm provides a way to trade the convergence rate with the number of subspaces used in the optimisation. Finally, when the number of subspaces is "sufficiently large", our algorithm's cumulative regret is at most $\mathcal{O}^{*}(\sqrt{T\gamma_T})$ as opposed to $\mathcal{O}^{*}(\sqrt{DT\gamma_T})$ for the GP-UCB of Srinivas et al. (2012), reducing a crucial factor $\sqrt{D}$ where $D$ being the dimensional number of input space.

Bayesian Optimization with Unknown Search Space

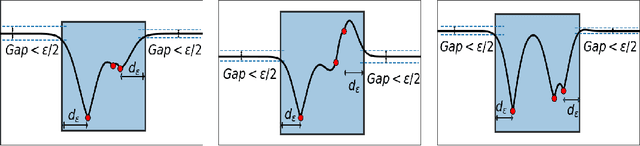
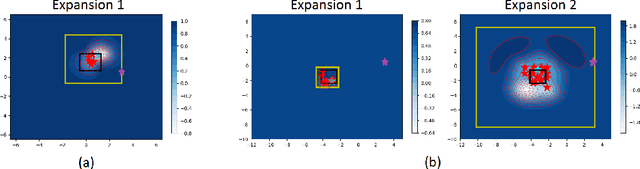
Applying Bayesian optimization in problems wherein the search space is unknown is challenging. To address this problem, we propose a systematic volume expansion strategy for the Bayesian optimization. We devise a strategy to guarantee that in iterative expansions of the search space, our method can find a point whose function value within epsilon of the objective function maximum. Without the need to specify any parameters, our algorithm automatically triggers a minimal expansion required iteratively. We derive analytic expressions for when to trigger the expansion and by how much to expand. We also provide theoretical analysis to show that our method achieves epsilon-accuracy after a finite number of iterations. We demonstrate our method on both benchmark test functions and machine learning hyper-parameter tuning tasks and demonstrate that our method outperforms baselines.

Learning Transferable Domain Priors for Safe Exploration in Reinforcement Learning

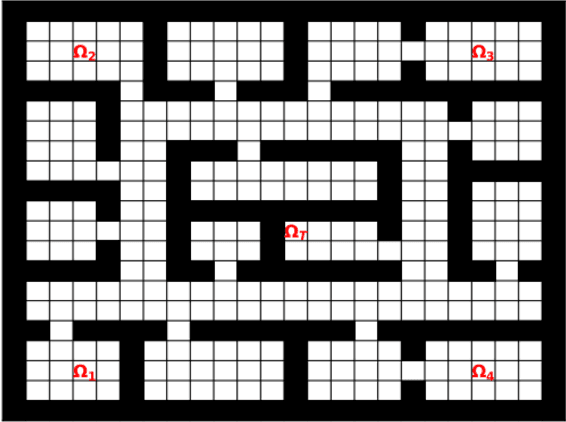
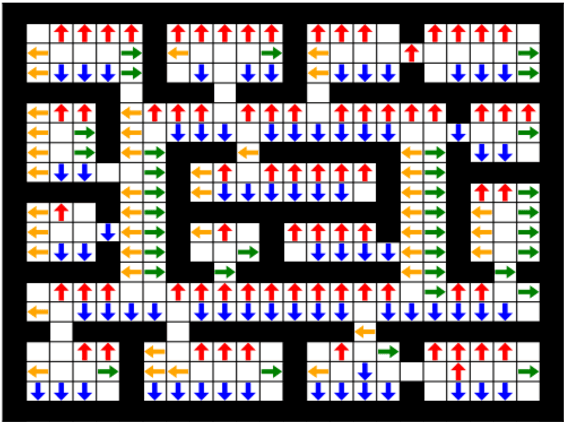
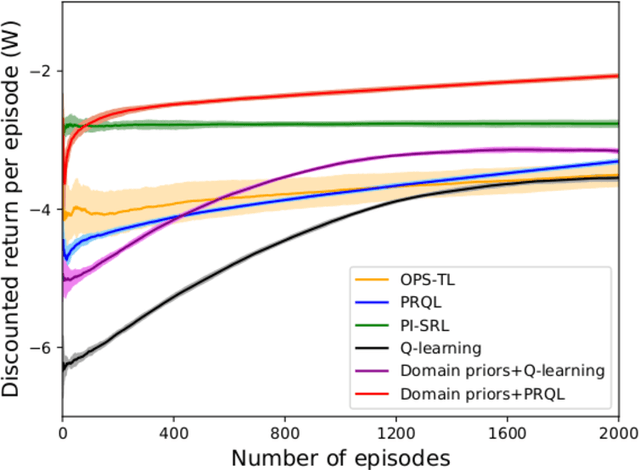
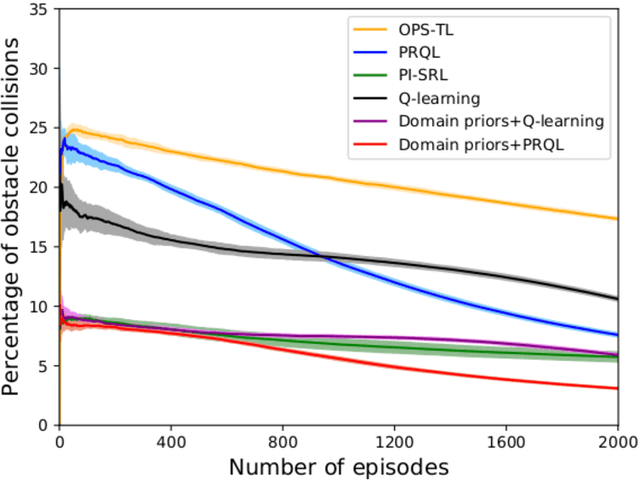
Prior access to domain knowledge could significantly improve the performance of a reinforcement learning agent. In particular, it could help agents avoid potentially catastrophic exploratory actions, which would otherwise have to be experienced during learning. In this work, we identify consistently undesirable actions in a set of previously learned tasks, and use pseudo-rewards associated with them to learn a prior policy. In addition to enabling safe exploratory behaviors in subsequent tasks in the domain, these priors are transferable to similar environments, and can be learned off-policy and in parallel with the learning of other tasks in the domain. We compare our approach to established, state-of-the-art algorithms in a grid-world navigation environment, and demonstrate that it exhibits a superior performance with respect to avoiding unsafe actions while learning to perform arbitrary tasks in the domain. We also present some theoretical analysis to support these results, and discuss the implications and some alternative formulations of this approach, which could also be useful to accelerate learning in certain scenarios.