Fast Training of Sinusoidal Neural Fields via Scaling Initialization

Neural fields are an emerging paradigm that represent data as continuous functions parameterized by neural networks. Despite many advantages, neural fields often have a high training cost, which prevents a broader adoption. In this paper, we focus on a popular family of neural fields, called sinusoidal neural fields (SNFs), and study how it should be initialized to maximize the training speed. We find that the standard initialization scheme for SNFs -- designed based on the signal propagation principle -- is suboptimal. In particular, we show that by simply multiplying each weight (except for the last layer) by a constant, we can accelerate SNF training by 10$\times$. This method, coined $\textit{weight scaling}$, consistently provides a significant speedup over various data domains, allowing the SNFs to train faster than more recently proposed architectures. To understand why the weight scaling works well, we conduct extensive theoretical and empirical analyses which reveal that the weight scaling not only resolves the spectral bias quite effectively but also enjoys a well-conditioned optimization trajectory.

In Search of a Data Transformation That Accelerates Neural Field Training

Neural field is an emerging paradigm in data representation that trains a neural network to approximate the given signal. A key obstacle that prevents its widespread adoption is the encoding speed-generating neural fields requires an overfitting of a neural network, which can take a significant number of SGD steps to reach the desired fidelity level. In this paper, we delve into the impacts of data transformations on the speed of neural field training, specifically focusing on how permuting pixel locations affect the convergence speed of SGD. Counterintuitively, we find that randomly permuting the pixel locations can considerably accelerate the training. To explain this phenomenon, we examine the neural field training through the lens of PSNR curves, loss landscapes, and error patterns. Our analyses suggest that the random pixel permutations remove the easy-to-fit patterns, which facilitate easy optimization in the early stage but hinder capturing fine details of the signal.

Hierarchically Decomposed Graph Convolutional Networks for Skeleton-Based Action Recognition

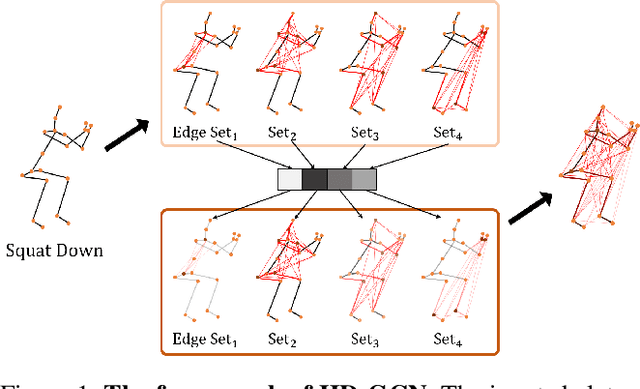
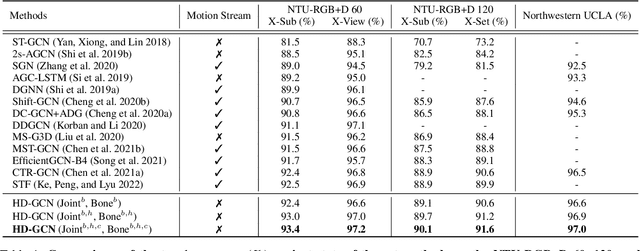
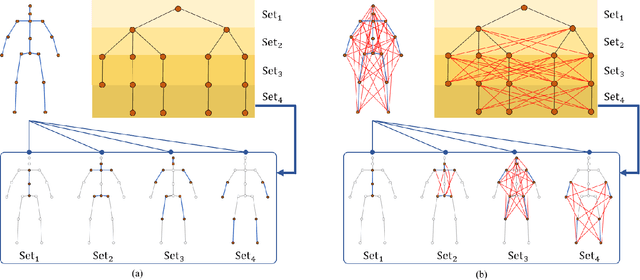
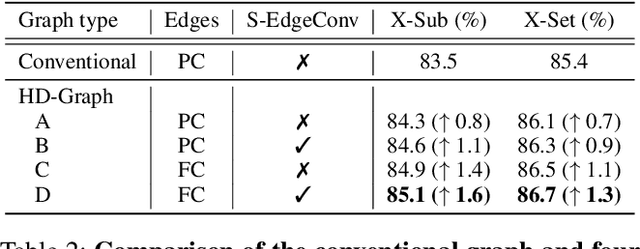
Graph convolutional networks (GCNs) are the most commonly used method for skeleton-based action recognition and have achieved remarkable performance. Generating adjacency matrices with semantically meaningful edges is particularly important for this task, but extracting such edges is challenging problem. To solve this, we propose a hierarchically decomposed graph convolutional network (HD-GCN) architecture with a novel hierarchically decomposed graph (HD-Graph). The proposed HD-GCN effectively decomposes every joint node into several sets to extract major adjacent and distant edges, and uses them to construct an HD-Graph containing those edges in the same semantic spaces of a human skeleton. In addition, we introduce an attention-guided hierarchy aggregation (A-HA) module to highlight the dominant hierarchical edge sets of the HD-Graph. Furthermore, we apply a new two-stream-three-graph ensemble method, which uses only joint and bone stream without any motion stream. The proposed model is evaluated and achieves state-of-the-art performance on three large, popular datasets: NTU-RGB+D 60, NTU-RGB+D 120, and Northwestern-UCLA. Finally, we demonstrate the effectiveness of our model with various comparative experiments.