Unsupervised Multi-source Domain Adaptation Without Access to Source Data

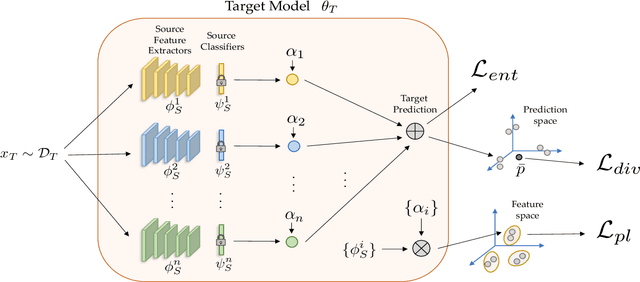
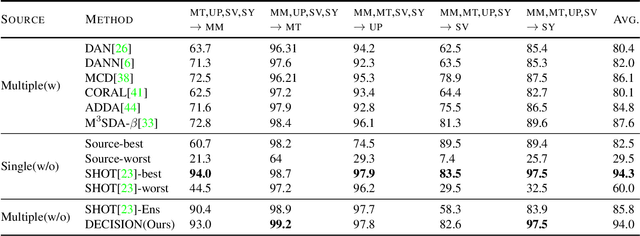
Unsupervised Domain Adaptation (UDA) aims to learn a predictor model for an unlabeled domain by transferring knowledge from a separate labeled source domain. However, most of these conventional UDA approaches make the strong assumption of having access to the source data during training, which may not be very practical due to privacy, security and storage concerns. A recent line of work addressed this problem and proposed an algorithm that transfers knowledge to the unlabeled target domain from a single source model without requiring access to the source data. However, for adaptation purposes, if there are multiple trained source models available to choose from, this method has to go through adapting each and every model individually, to check for the best source. Thus, we ask the question: can we find the optimal combination of source models, with no source data and without target labels, whose performance is no worse than the single best source? To answer this, we propose a novel and efficient algorithm which automatically combines the source models with suitable weights in such a way that it performs at least as good as the best source model. We provide intuitive theoretical insights to justify our claim. Furthermore, extensive experiments are conducted on several benchmark datasets to show the effectiveness of our algorithm, where in most cases, our method not only reaches best source accuracy but also outperforms it.

Label-Imbalanced and Group-Sensitive Classification under Overparameterization

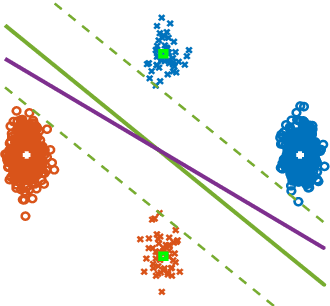
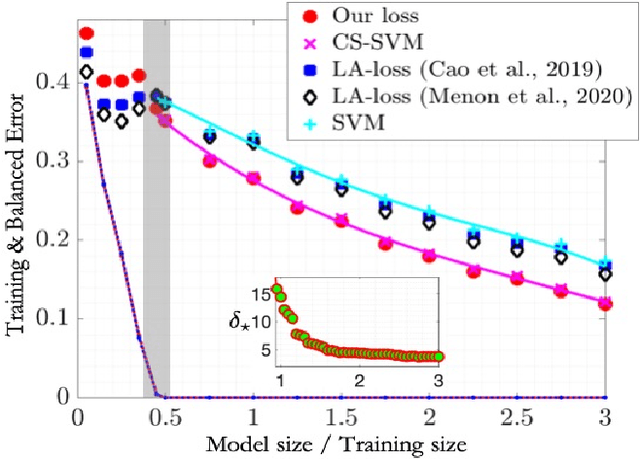
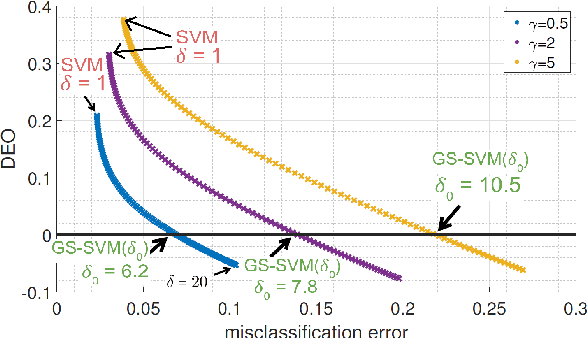
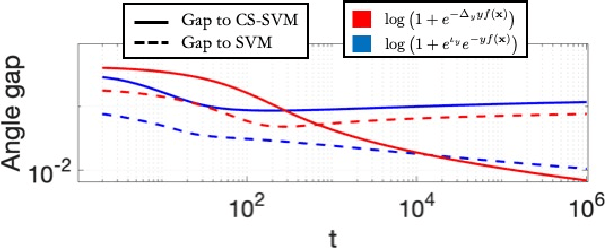
Label-imbalanced and group-sensitive classification seeks to appropriately modify standard training algorithms to optimize relevant metrics such as balanced error and/or equal opportunity. For label imbalances, recent works have proposed a logit-adjusted loss modification to standard empirical risk minimization. We show that this might be ineffective in general and, in particular so, in the overparameterized regime where training continues in the zero training-error regime. Specifically for binary linear classification of a separable dataset, we show that the modified loss converges to the max-margin SVM classifier despite the logit adjustment. Instead, we propose a more general vector-scaling loss that directly relates to the cost-sensitive SVM (CS-SVM), thus favoring larger margin to the minority class. Through an insightful sharp asymptotic analysis for a Gaussian-mixtures data model, we demonstrate the efficacy of CS-SVM in balancing the errors of the minority/majority classes. Our analysis also leads to a simple strategy for optimally tuning the involved margin-ratio parameter. Then, we show how our results extend naturally to binary classification with sensitive groups, thus treating the two common types of imbalances (label/group) in a unifying way. We corroborate our theoretical findings with numerical experiments on both synthetic and real-world datasets.

Sample Efficient Subspace-based Representations for Nonlinear Meta-Learning

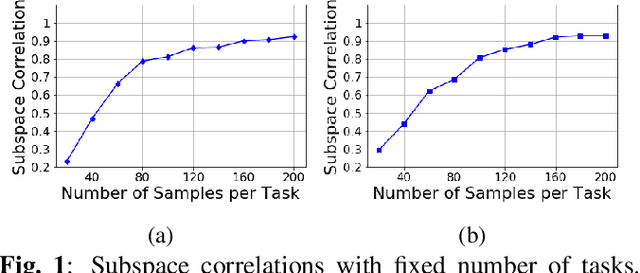
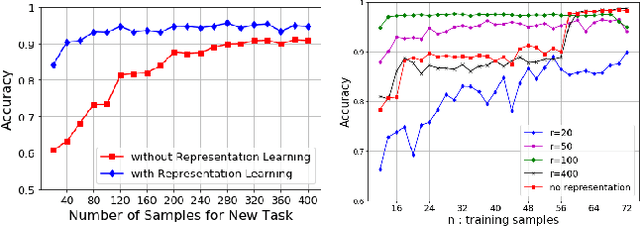
Constructing good representations is critical for learning complex tasks in a sample efficient manner. In the context of meta-learning, representations can be constructed from common patterns of previously seen tasks so that a future task can be learned quickly. While recent works show the benefit of subspace-based representations, such results are limited to linear-regression tasks. This work explores a more general class of nonlinear tasks with applications ranging from binary classification, generalized linear models and neural nets. We prove that subspace-based representations can be learned in a sample-efficient manner and provably benefit future tasks in terms of sample complexity. Numerical results verify the theoretical predictions in classification and neural-network regression tasks.

Super-Convergence with an Unstable Learning Rate

Conventional wisdom dictates that learning rate should be in the stable regime so that gradient-based algorithms don't blow up. This note introduces a simple scenario where an unstable learning rate scheme leads to a super fast convergence, with the convergence rate depending only logarithmically on the condition number of the problem. Our scheme uses a Cyclical Learning Rate where we periodically take one large unstable step and several small stable steps to compensate for the instability. These findings also help explain the empirical observations of [Smith and Topin, 2019] where they claim CLR with a large maximum learning rate leads to "super-convergence". We prove that our scheme excels in the problems where Hessian exhibits a bimodal spectrum and the eigenvalues can be grouped into two clusters (small and large). The unstable step is the key to enabling fast convergence over the small eigen-spectrum.

Provable Benefits of Overparameterization in Model Compression: From Double Descent to Pruning Neural Networks

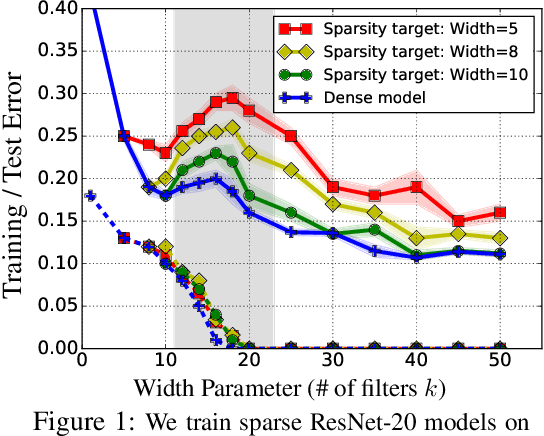
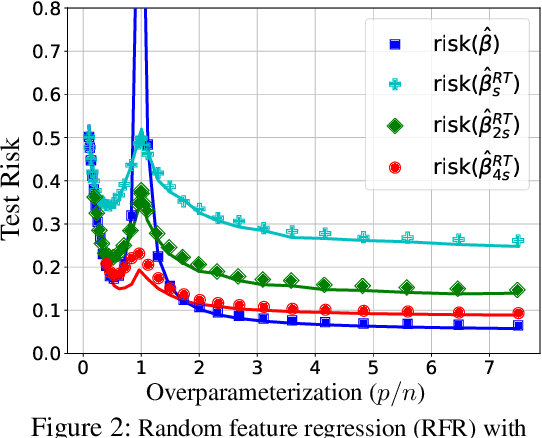
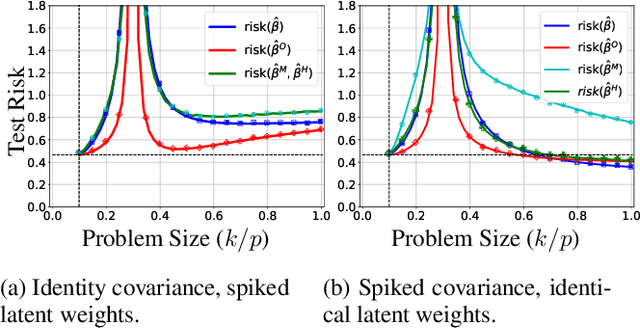
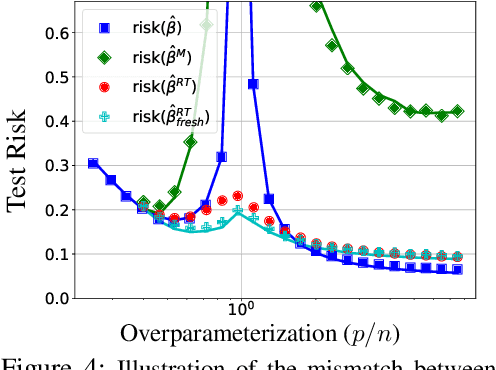
Deep networks are typically trained with many more parameters than the size of the training dataset. Recent empirical evidence indicates that the practice of overparameterization not only benefits training large models, but also assists - perhaps counterintuitively - building lightweight models. Specifically, it suggests that overparameterization benefits model pruning / sparsification. This paper sheds light on these empirical findings by theoretically characterizing the high-dimensional asymptotics of model pruning in the overparameterized regime. The theory presented addresses the following core question: "should one train a small model from the beginning, or first train a large model and then prune?". We analytically identify regimes in which, even if the location of the most informative features is known, we are better off fitting a large model and then pruning rather than simply training with the known informative features. This leads to a new double descent in the training of sparse models: growing the original model, while preserving the target sparsity, improves the test accuracy as one moves beyond the overparameterization threshold. Our analysis further reveals the benefit of retraining by relating it to feature correlations. We find that the above phenomena are already present in linear and random-features models. Our technical approach advances the toolset of high-dimensional analysis and precisely characterizes the asymptotic distribution of over-parameterized least-squares. The intuition gained by analytically studying simpler models is numerically verified on neural networks.

On the Marginal Benefit of Active Learning: Does Self-Supervision Eat Its Cake?

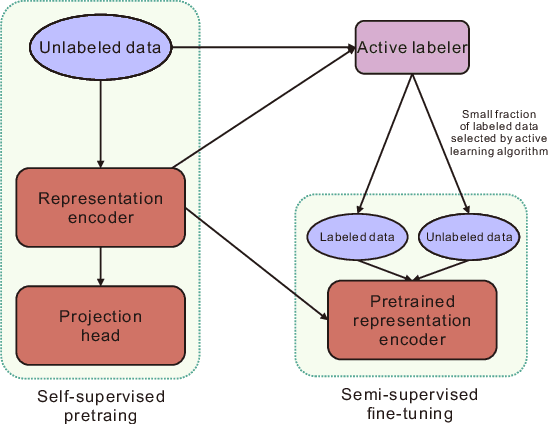
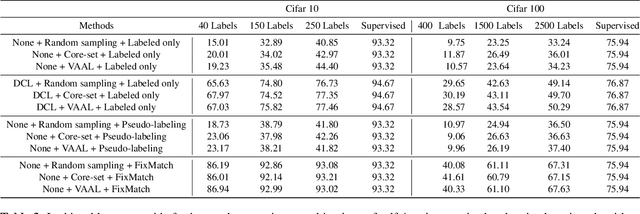
Active learning is the set of techniques for intelligently labeling large unlabeled datasets to reduce the labeling effort. In parallel, recent developments in self-supervised and semi-supervised learning (S4L) provide powerful techniques, based on data-augmentation, contrastive learning, and self-training, that enable superior utilization of unlabeled data which led to a significant reduction in required labeling in the standard machine learning benchmarks. A natural question is whether these paradigms can be unified to obtain superior results. To this aim, this paper provides a novel algorithmic framework integrating self-supervised pretraining, active learning, and consistency-regularized self-training. We conduct extensive experiments with our framework on CIFAR10 and CIFAR100 datasets. These experiments enable us to isolate and assess the benefits of individual components which are evaluated using state-of-the-art methods (e.g.~Core-Set, VAAL, simCLR, FixMatch). Our experiments reveal two key insights: (i) Self-supervised pre-training significantly improves semi-supervised learning, especially in the few-label regime, (ii) The benefit of active learning is undermined and subsumed by S4L techniques. Specifically, we fail to observe any additional benefit of state-of-the-art active learning algorithms when combined with state-of-the-art S4L techniques.

Theoretical Insights Into Multiclass Classification: A High-dimensional Asymptotic View

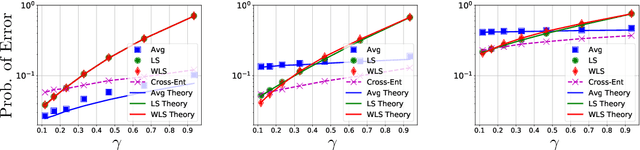
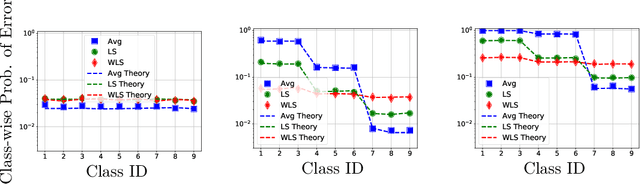
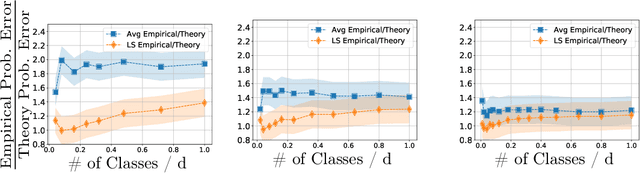
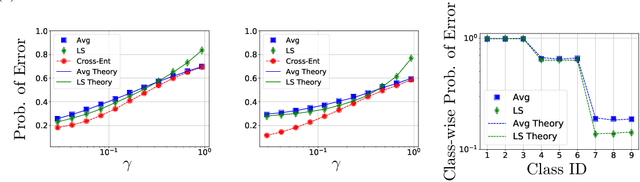
Contemporary machine learning applications often involve classification tasks with many classes. Despite their extensive use, a precise understanding of the statistical properties and behavior of classification algorithms is still missing, especially in modern regimes where the number of classes is rather large. In this paper, we take a step in this direction by providing the first asymptotically precise analysis of linear multiclass classification. Our theoretical analysis allows us to precisely characterize how the test error varies over different training algorithms, data distributions, problem dimensions as well as number of classes, inter/intra class correlations and class priors. Specifically, our analysis reveals that the classification accuracy is highly distribution-dependent with different algorithms achieving optimal performance for different data distributions and/or training/features sizes. Unlike linear regression/binary classification, the test error in multiclass classification relies on intricate functions of the trained model (e.g., correlation between some of the trained weights) whose asymptotic behavior is difficult to characterize. This challenge is already present in simple classifiers, such as those minimizing a square loss. Our novel theoretical techniques allow us to overcome some of these challenges. The insights gained may pave the way for a precise understanding of other classification algorithms beyond those studied in this paper.

Unsupervised Paraphrasing via Deep Reinforcement Learning

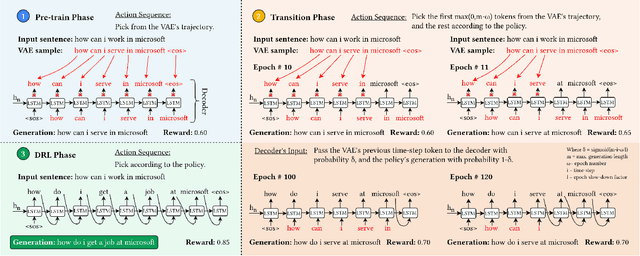
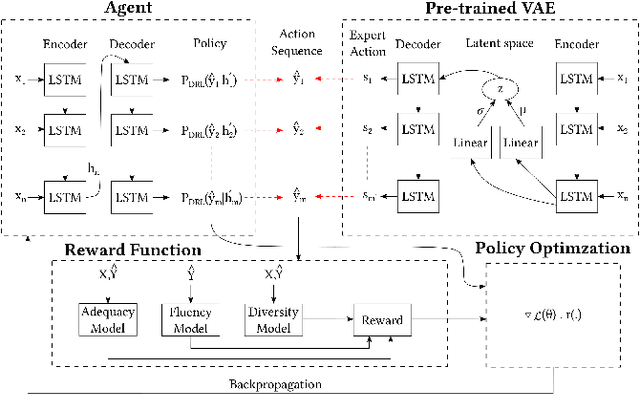
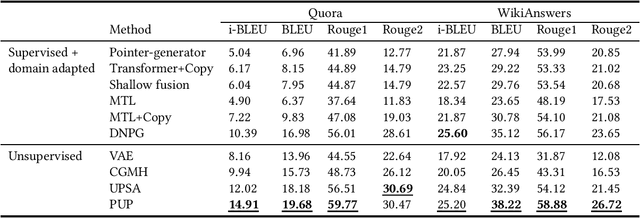
Paraphrasing is expressing the meaning of an input sentence in different wording while maintaining fluency (i.e., grammatical and syntactical correctness). Most existing work on paraphrasing use supervised models that are limited to specific domains (e.g., image captions). Such models can neither be straightforwardly transferred to other domains nor generalize well, and creating labeled training data for new domains is expensive and laborious. The need for paraphrasing across different domains and the scarcity of labeled training data in many such domains call for exploring unsupervised paraphrase generation methods. We propose Progressive Unsupervised Paraphrasing (PUP): a novel unsupervised paraphrase generation method based on deep reinforcement learning (DRL). PUP uses a variational autoencoder (trained using a non-parallel corpus) to generate a seed paraphrase that warm-starts the DRL model. Then, PUP progressively tunes the seed paraphrase guided by our novel reward function which combines semantic adequacy, language fluency, and expression diversity measures to quantify the quality of the generated paraphrases in each iteration without needing parallel sentences. Our extensive experimental evaluation shows that PUP outperforms unsupervised state-of-the-art paraphrasing techniques in terms of both automatic metrics and user studies on four real datasets. We also show that PUP outperforms domain-adapted supervised algorithms on several datasets. Our evaluation also shows that PUP achieves a great trade-off between semantic similarity and diversity of expression.

Statistical and Algorithmic Insights for Semi-supervised Learning with Self-training

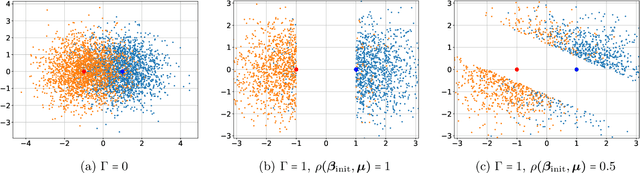
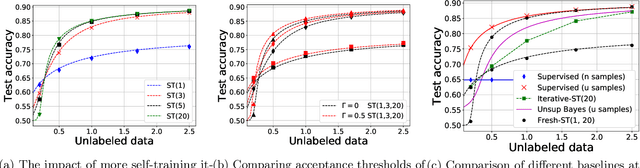
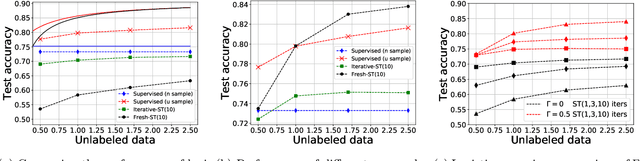
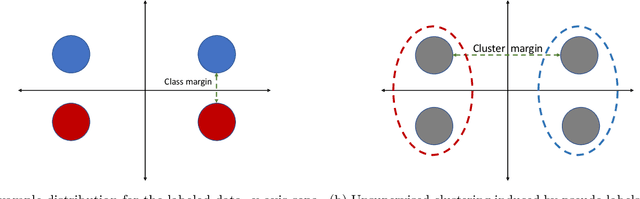
Self-training is a classical approach in semi-supervised learning which is successfully applied to a variety of machine learning problems. Self-training algorithm generates pseudo-labels for the unlabeled examples and progressively refines these pseudo-labels which hopefully coincides with the actual labels. This work provides theoretical insights into self-training algorithm with a focus on linear classifiers. We first investigate Gaussian mixture models and provide a sharp non-asymptotic finite-sample characterization of the self-training iterations. Our analysis reveals the provable benefits of rejecting samples with low confidence and demonstrates that self-training iterations gracefully improve the model accuracy even if they do get stuck in sub-optimal fixed points. We then demonstrate that regularization and class margin (i.e. separation) is provably important for the success and lack of regularization may prevent self-training from identifying the core features in the data. Finally, we discuss statistical aspects of empirical risk minimization with self-training for general distributions. We show how a purely unsupervised notion of generalization based on self-training based clustering can be formalized based on cluster margin. We then establish a connection between self-training based semi-supervision and the more general problem of learning with heterogenous data and weak supervision.

Exploring Weight Importance and Hessian Bias in Model Pruning

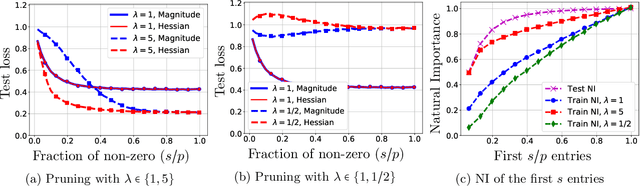
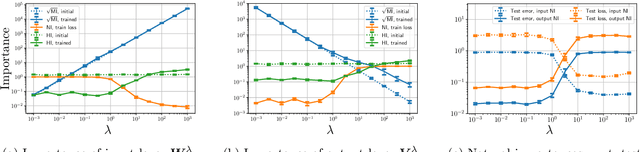
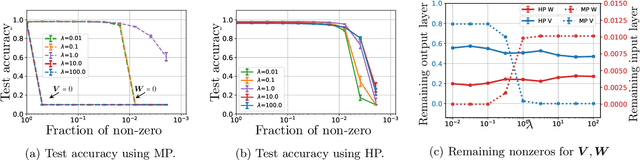
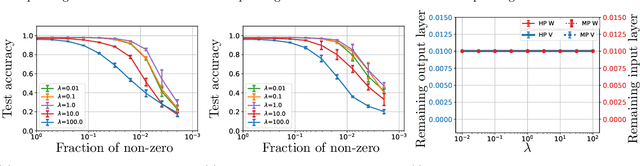
Model pruning is an essential procedure for building compact and computationally-efficient machine learning models. A key feature of a good pruning algorithm is that it accurately quantifies the relative importance of the model weights. While model pruning has a rich history, we still don't have a full grasp of the pruning mechanics even for relatively simple problems involving linear models or shallow neural nets. In this work, we provide a principled exploration of pruning by building on a natural notion of importance. For linear models, we show that this notion of importance is captured by covariance scaling which connects to the well-known Hessian-based pruning. We then derive asymptotic formulas that allow us to precisely compare the performance of different pruning methods. For neural networks, we demonstrate that the importance can be at odds with larger magnitudes and proper initialization is critical for magnitude-based pruning. Specifically, we identify settings in which weights become more important despite becoming smaller, which in turn leads to a catastrophic failure of magnitude-based pruning. Our results also elucidate that implicit regularization in the form of Hessian structure has a catalytic role in identifying the important weights, which dictate the pruning performance.