Flow matching Operators for Residual-Augmented Probabilistic Learning of Partial Differential Equations

Learning probabilistic surrogates for partial differential equations remains challenging in data-scarce regimes: neural operators require large amounts of high-fidelity data, while generative approaches typically sacrifice resolution invariance. We formulate flow matching in an infinite-dimensional function space to learn a probabilistic transport that maps low-fidelity approximations to the manifold of high-fidelity PDE solutions via learned residual corrections. We develop a conditional neural operator architecture based on feature-wise linear modulation for flow matching vector fields directly in function space, enabling inference at arbitrary spatial resolutions without retraining. To improve stability and representational control of the induced neural ODE, we parameterize the flow vector field as a sum of a linear operator and a nonlinear operator, combining lightweight linear components with a conditioned Fourier neural operator for expressive, input-dependent dynamics. We then formulate a residual-augmented learning strategy where the flow model learns probabilistic corrections from inexpensive low-fidelity surrogates to high-fidelity solutions, rather than learning the full solution mapping from scratch. Finally, we derive tractable training objectives that extend conditional flow matching to the operator setting with input-function-dependent couplings. To demonstrate the effectiveness of our approach, we present numerical experiments on a range of PDEs, including the 1D advection and Burgers' equation, and a 2D Darcy flow problem for flow through a porous medium. We show that the proposed method can accurately learn solution operators across different resolutions and fidelities and produces uncertainty estimates that appropriately reflect model confidence, even when trained on limited high-fidelity data.

Multi-fidelity reinforcement learning framework for shape optimization

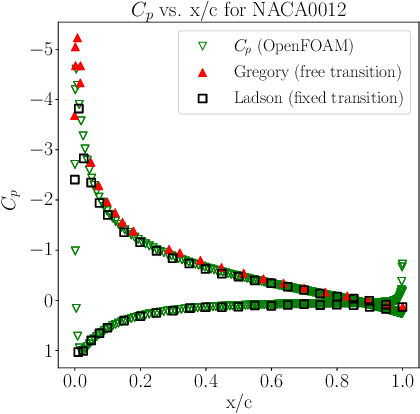
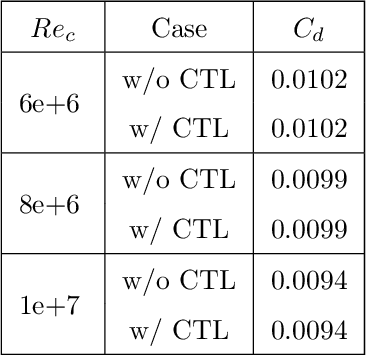
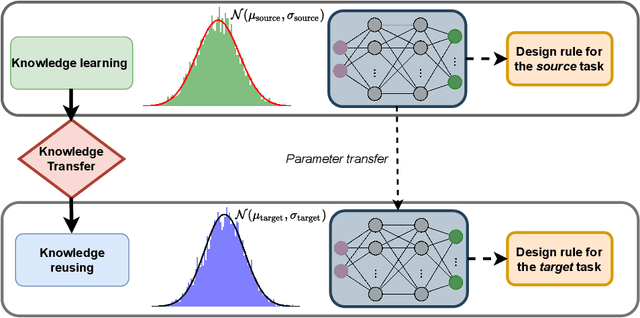
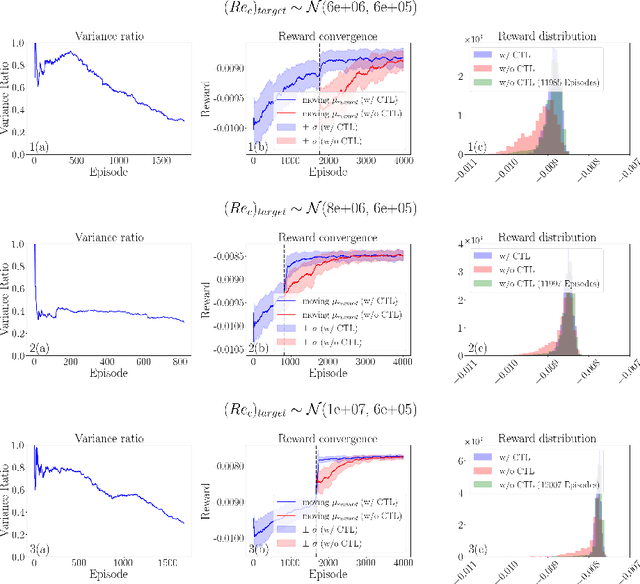
Deep reinforcement learning (DRL) is a promising outer-loop intelligence paradigm which can deploy problem solving strategies for complex tasks. Consequently, DRL has been utilized for several scientific applications, specifically in cases where classical optimization or control methods are limited. One key limitation of conventional DRL methods is their episode-hungry nature which proves to be a bottleneck for tasks which involve costly evaluations of a numerical forward model. In this article, we address this limitation of DRL by introducing a controlled transfer learning framework that leverages a multi-fidelity simulation setting. Our strategy is deployed for an airfoil shape optimization problem at high Reynolds numbers, where our framework can learn an optimal policy for generating efficient airfoil shapes by gathering knowledge from multi-fidelity environments and reduces computational costs by over 30\%. Furthermore, our formulation promotes policy exploration and generalization to new environments, thereby preventing over-fitting to data from solely one fidelity. Our results demonstrate this framework's applicability to other scientific DRL scenarios where multi-fidelity environments can be used for policy learning.