Non-Trivial Query Sampling For Efficient Learning To Plan

In recent years, learning-based approaches have revolutionized motion planning. The data generation process for these methods involves caching a large number of high quality paths for different queries (start, goal pairs) in various environments. Conventionally, a uniform random strategy is used for sampling these queries. However, this leads to inclusion of "trivial paths" in the dataset (e.g.,, straight line paths in case of length-optimal planning), which can be solved efficiently if the planner has access to a steering function. This work proposes a "non-trivial" query sampling procedure to add more complex paths in the dataset. Numerical experiments show that a higher success rate can be attained for neural planners trained on such a non-trivial dataset.

LES: Locally Exploitative Sampling for Robot Path Planning

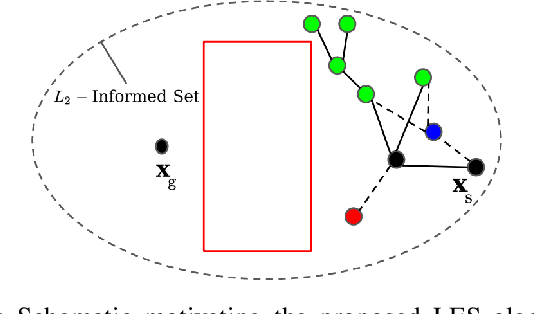
Sampling-based algorithms solve the path planning problem by generating random samples in the search-space and incrementally growing a connectivity graph or a tree. Conventionally, the sampling strategy used in these algorithms is biased towards exploration to acquire information about the search-space. In contrast, this work proposes an optimization-based procedure that generates new samples to improve the cost-to-come value of vertices in a neighborhood. The application of proposed algorithm adds an exploitative-bias to sampling and results in a faster convergence to the optimal solution compared to other state-of-the-art sampling techniques. This is demonstrated using benchmarking experiments performed fora variety of higher dimensional robotic planning tasks.

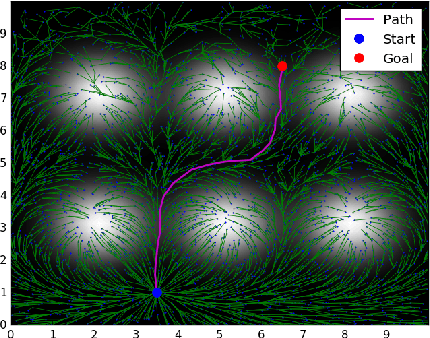
Time-Informed Exploration For Robot Motion Planning

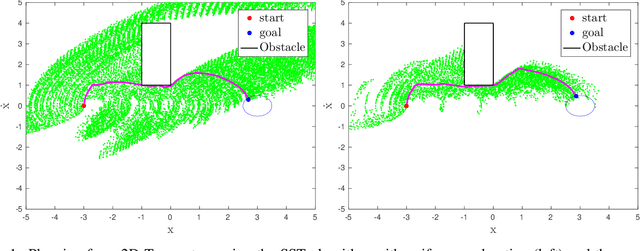
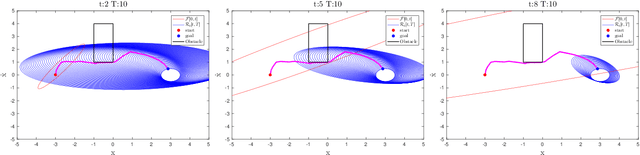
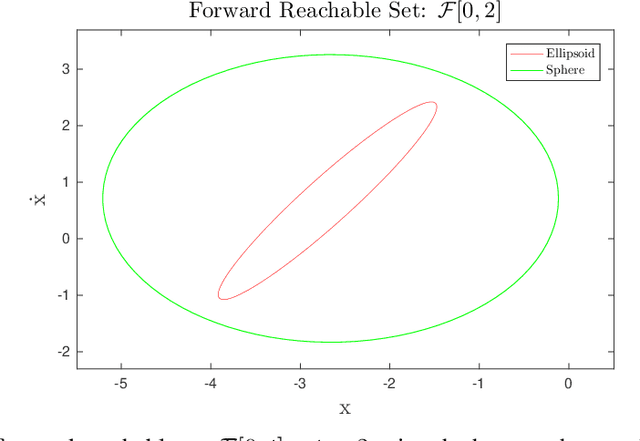
Anytime sampling-based methods are an attractive technique for solving kino-dynamic motion planning problems. These algorithms scale well to higher dimensions and can efficiently handle state and control constraints. However, an intelligent exploration strategy is required to accelerate their convergence and avoid redundant computations. This work defines a "Time Informed Set", using ideas from reachability analysis, that focuses the search for time-optimal kino-dynamic planning after an initial solution is found. Such a Time Informed Set includes all trajectories that can potentially improve the current best solution. Exploration outside this set is hence redundant. Benchmarking experiments show that an exploration strategy based on the Time Informed Set can accelerate the convergence of sampling-based kino-dynamic motion planners.

Relevant Region Exploration On General Cost-maps For Sampling-Based Motion Planning

Asymptotically optimal sampling-based planners require an intelligent exploration strategy to accelerate convergence. After an initial solution is found, a necessary condition for improvement is to generate new samples in the so-called "Informed Set". However, Informed Sampling can be ineffective in focusing search if the chosen heuristic fails to provide a good estimate of the solution cost. This work proposes an algorithm to sample the "Relevant Region" instead, which is a subset of the Informed Set. The Relevant Region utilizes cost-to-come information from the planner's tree structure, reduces dependence on the heuristic, and further focuses the search. Benchmarking tests in uniform and general cost-space settings demonstrate the efficacy of Relevant Region sampling.