Neural Ordinary Differential Equation Model for Evolutionary Subspace Clustering and Its Applications

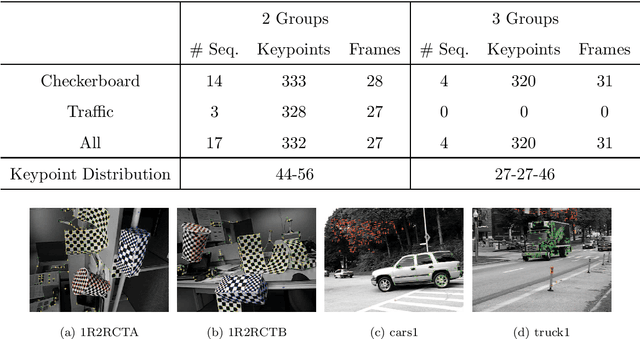
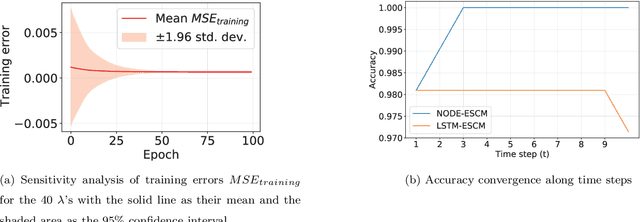
The neural ordinary differential equation (neural ODE) model has attracted increasing attention in time series analysis for its capability to process irregular time steps, i.e., data are not observed over equally-spaced time intervals. In multi-dimensional time series analysis, a task is to conduct evolutionary subspace clustering, aiming at clustering temporal data according to their evolving low-dimensional subspace structures. Many existing methods can only process time series with regular time steps while time series are unevenly sampled in many situations such as missing data. In this paper, we propose a neural ODE model for evolutionary subspace clustering to overcome this limitation and a new objective function with subspace self-expressiveness constraint is introduced. We demonstrate that this method can not only interpolate data at any time step for the evolutionary subspace clustering task, but also achieve higher accuracy than other state-of-the-art evolutionary subspace clustering methods. Both synthetic and real-world data are used to illustrate the efficacy of our proposed method.

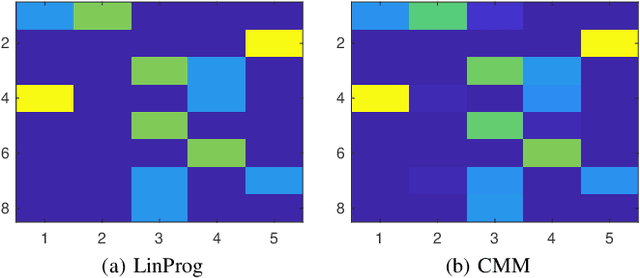
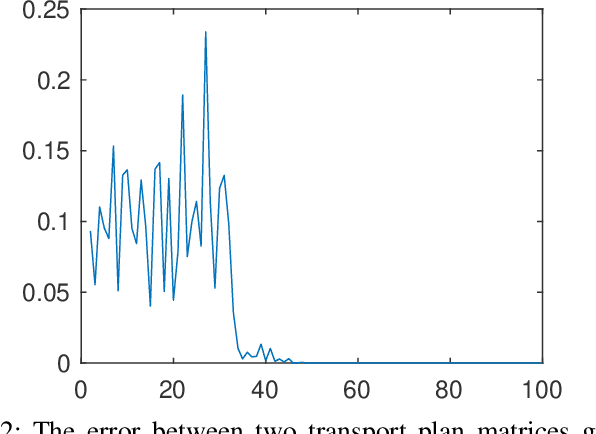
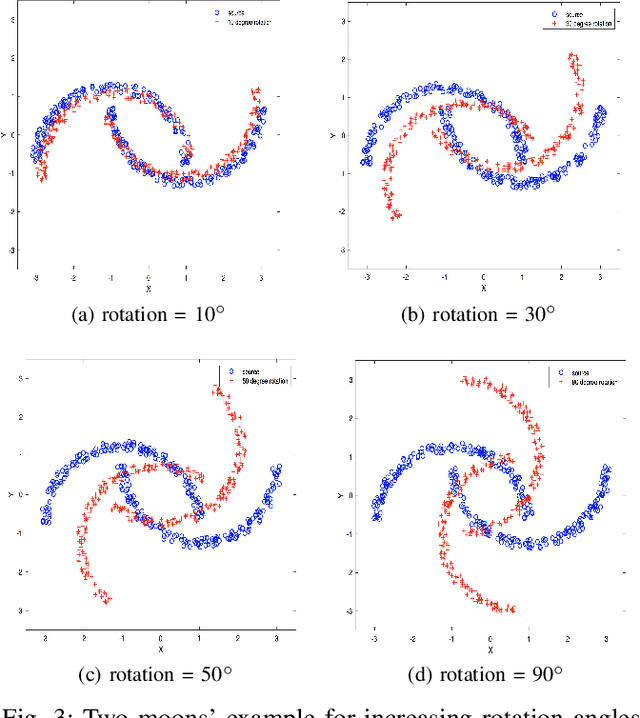
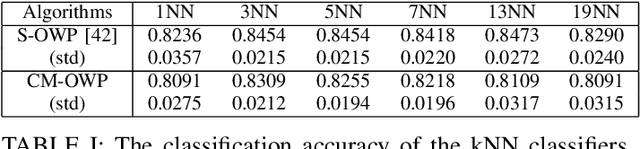
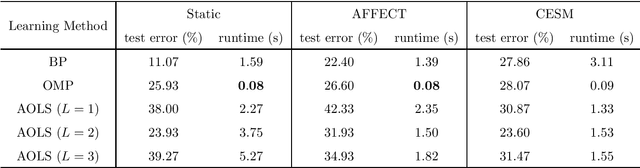
Coupling Matrix Manifolds and Their Applications in Optimal Transport

Optimal transport (OT) is a powerful tool for measuring the distance between two defined probability distributions. In this paper, we develop a new manifold named the coupling matrix manifold (CMM), where each point on CMM can be regarded as the transportation plan of the OT problem. We firstly explore the Riemannian geometry of CMM with the metric expressed by the Fisher information. These geometrical features of CMM have paved the way for developing numerical Riemannian optimization algorithms such as Riemannian gradient descent and Riemannian trust-region algorithms, forming a uniform optimization method for all types of OT problems. The proposed method is then applied to solve several OT problems studied by previous literature. The results of the numerical experiments illustrate that the optimization algorithms that are based on the method proposed in this paper are comparable to the classic ones, for example, the Sinkhorn algorithm, while outperforming other state-of-the-art algorithms without considering the geometry information, especially in the case of non-entropy optimal transport.

Tensor-Train Parameterization for Ultra Dimensionality Reduction

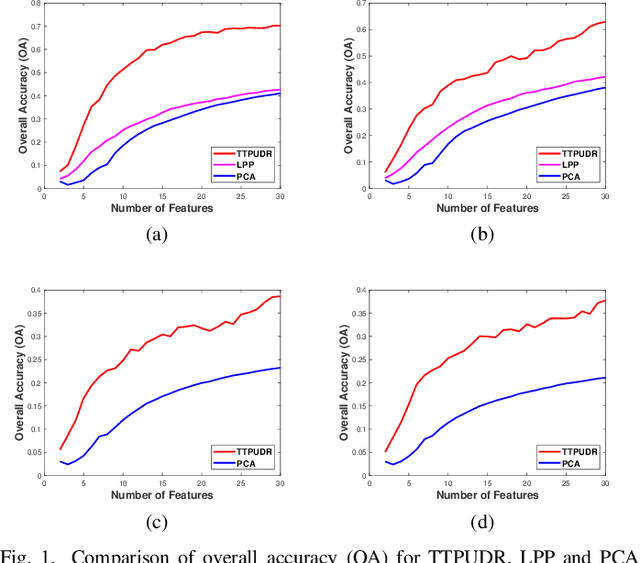
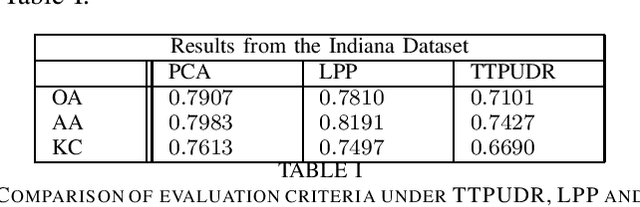
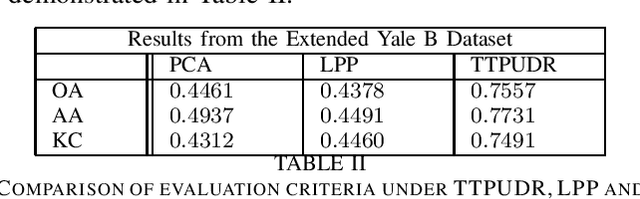
Locality preserving projections (LPP) are a classical dimensionality reduction method based on data graph information. However, LPP is still responsive to extreme outliers. LPP aiming for vectorial data may undermine data structural information when it is applied to multidimensional data. Besides, it assumes the dimension of data to be smaller than the number of instances, which is not suitable for high-dimensional data. For high-dimensional data analysis, the tensor-train decomposition is proved to be able to efficiently and effectively capture the spatial relations. Thus, we propose a tensor-train parameterization for ultra dimensionality reduction (TTPUDR) in which the traditional LPP mapping is tensorized in terms of tensor-trains and the LPP objective is replaced with the Frobenius norm to increase the robustness of the model. The manifold optimization technique is utilized to solve the new model. The performance of TTPUDR is assessed on classification problems and TTPUDR significantly outperforms the past methods and the several state-of-the-art methods.