Maximal Causes for Exponential Family Observables

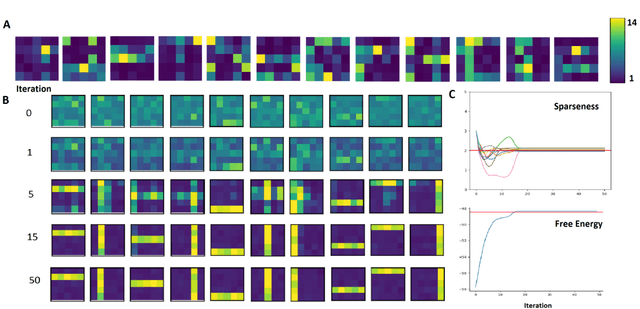
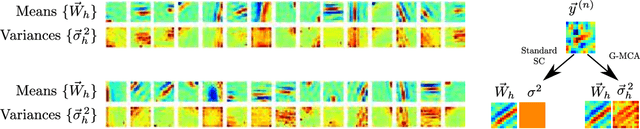
The data model of standard sparse coding assumes a weighted linear summation of latents to determine the mean of Gaussian observation noise. However, such a linear summation of latents is often at odds with non-Gaussian observables (e.g., means of the Bernoulli distribution have to lie in the unit interval), and also in the Gaussian case it can be difficult to justify for many types of data. Alternative superposition models (i.e., links between latents and observables) have therefore been investigated repeatedly. Here we show that using the maximum instead of a linear sum to link latents to observables allows for the derivation of very general and concise parameter update equations. Concretely, we derive a set of update equations that has the same functional form for all distributions of the exponential family (given that derivatives w.r.t. their parameters can be taken). Our results consequently allow for the development of latent variable models for commonly as well as for unusually distributed data. We numerically verify our analytical result assuming standard Gaussian, Gamma, Poisson, Bernoulli and Exponential distributions and point to some potential applications.

Solving the L1 regularized least square problem via a box-constrained smooth minimization

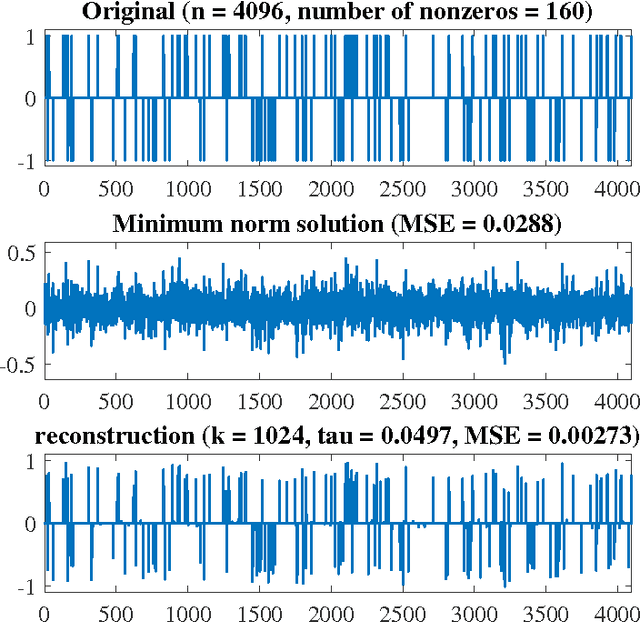
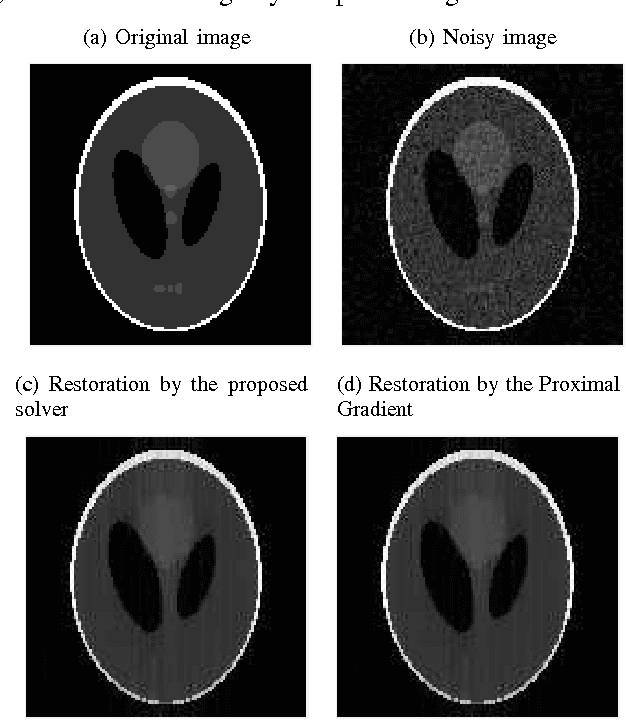
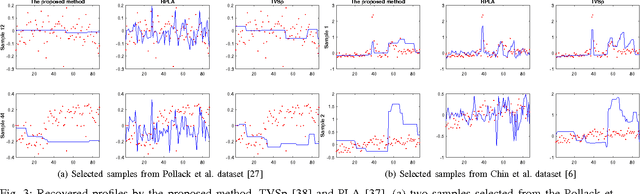
In this paper, an equivalent smooth minimization for the L1 regularized least square problem is proposed. The proposed problem is a convex box-constrained smooth minimization which allows applying fast optimization methods to find its solution. Further, it is investigated that the property "the dual of dual is primal" holds for the L1 regularized least square problem. A solver for the smooth problem is proposed, and its affinity to the proximal gradient is shown. Finally, the experiments on L1 and total variation regularized problems are performed, and the corresponding results are reported.