Personalized Prediction Models for Changes in Knee Pain among Patients with Osteoarthritis Participating in Supervised Exercise and Education

Knee osteoarthritis (OA) is a widespread chronic condition that impairs mobility and diminishes quality of life. Despite the proven benefits of exercise therapy and patient education in managing the OA symptoms pain and functional limitations, these strategies are often underutilized. Personalized outcome prediction models can help motivate and engage patients, but the accuracy of existing models in predicting changes in knee pain remains insufficiently examined. To validate existing models and introduce a concise personalized model predicting changes in knee pain before to after participating in a supervised education and exercise therapy program (GLA:D) for knee OA patients. Our models use self-reported patient information and functional measures. To refine the number of variables, we evaluated the variable importance and applied clinical reasoning. We trained random forest regression models and compared the rate of true predictions of our models with those utilizing average values. We evaluated the performance of a full, continuous, and concise model including all 34, all 11 continuous, and the six most predictive variables respectively. All three models performed similarly and were comparable to the existing model, with R-squares of 0.31-0.32 and RMSEs of 18.65-18.85 - despite our increased sample size. Allowing a deviation of 15 VAS points from the true change in pain, our concise model and utilizing the average values estimated the change in pain at 58% and 51% correctly, respectively. Our supplementary analysis led to similar outcomes. Our concise personalized prediction model more accurately predicts changes in knee pain following the GLA:D program compared to average pain improvement values. Neither the increase in sample size nor the inclusion of additional variables improved previous models. To improve predictions, new variables beyond those in the GLA:D are required.

Recent Trends in the Use of Statistical Tests for Comparing Swarm and Evolutionary Computing Algorithms: Practical Guidelines and a Critical Review

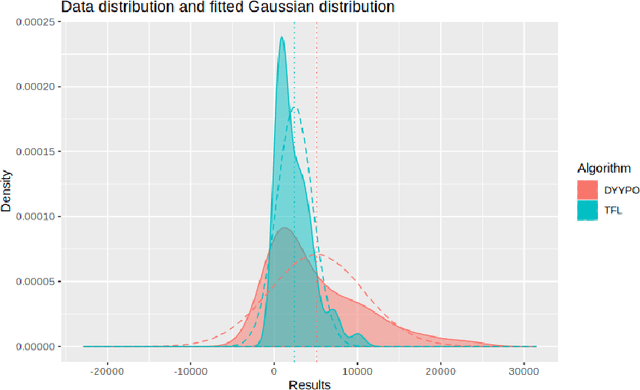
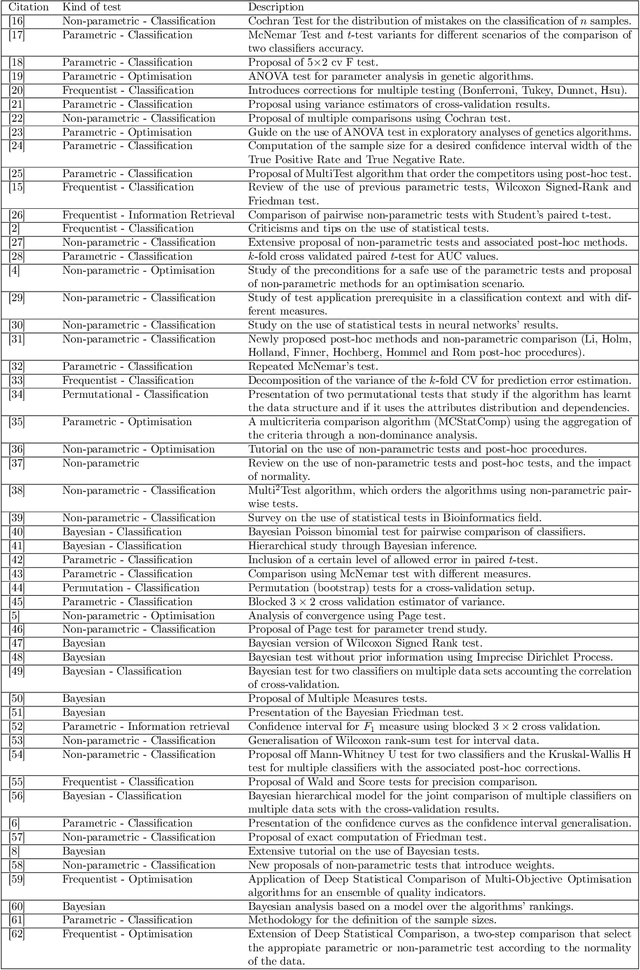
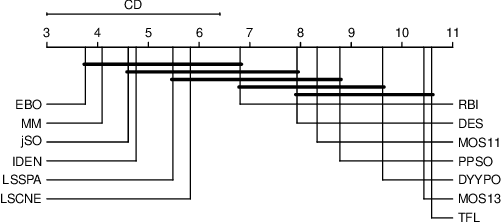
A key aspect of the design of evolutionary and swarm intelligence algorithms is studying their performance. Statistical comparisons are also a crucial part which allows for reliable conclusions to be drawn. In the present paper we gather and examine the approaches taken from different perspectives to summarise the assumptions made by these statistical tests, the conclusions reached and the steps followed to perform them correctly. In this paper, we conduct a survey on the current trends of the proposals of statistical analyses for the comparison of algorithms of computational intelligence and include a description of the statistical background of these tests. We illustrate the use of the most common tests in the context of the Competition on single-objective real parameter optimisation of the IEEE Congress on Evolutionary Computation (CEC) 2017 and describe the main advantages and drawbacks of the use of each kind of test and put forward some recommendations concerning their use.

Parallel and Communication Avoiding Least Angle Regression

We are interested in parallelizing the Least Angle Regression (LARS) algorithm for fitting linear regression models to high-dimensional data. We consider two parallel and communication avoiding versions of the basic LARS algorithm. The two algorithms apply to data that have different layout patterns (one is appropriate for row-partitioned data, and the other is appropriate for column-partitioned data), and they have different asymptotic costs and practical performance. The first is bLARS, a block version of LARS algorithm where we update b columns at each iteration. Assuming that the data are row-partitioned, bLARS reduces the number of arithmetic operations, latency, and bandwidth by a factor of b. The second is Tournament-bLARS (T-bLARS), a tournament version of LARS, in which case processors compete, by running several LARS computations in parallel, to choose b new columns to be added into the solution. Assuming that the data are column-partitioned, T-bLARS reduces latency by a factor of b. Similarly to LARS, our proposed methods generate a sequence of linear models. We present extensive numerical experiments that illustrate speed-ups up to 25x compared to LARS.

PaFiMoCS: Particle Filtered Modified-CS and Applications in Visual Tracking across Illumination Change

We study the problem of tracking (causally estimating) a time sequence of sparse spatial signals with changing sparsity patterns, as well as other unknown states, from a sequence of nonlinear observations corrupted by (possibly) non-Gaussian noise. In many applications, particularly those in visual tracking, the unknown state can be split into a small dimensional part, e.g. global motion, and a spatial signal, e.g. illumination or shape deformation. The spatial signal is often well modeled as being sparse in some domain. For a long sequence, its sparsity pattern can change over time, although the changes are usually slow. To address the above problem, we propose a novel solution approach called Particle Filtered Modified-CS (PaFiMoCS). The key idea of PaFiMoCS is to importance sample for the small dimensional state vector, while replacing importance sampling by slow sparsity pattern change constrained posterior mode tracking for recovering the sparse spatial signal. We show that the problem of tracking moving objects across spatially varying illumination change is an example of the above problem and explain how to design PaFiMoCS for it. Experiments on both simulated data as well as on real videos with significant illumination changes demonstrate the superiority of the proposed algorithm as compared with existing particle filter based tracking algorithms.