Agro-STAY : Collecte de données et analyse des informations en agriculture alternative issues de YouTube

To address the current crises (climatic, social, economic), the self-sufficiency -- a set of practices that combine energy sobriety, self-production of food and energy, and self-construction - arouses an increasing interest. The CNRS STAY project (Savoirs Techniques pour l'Auto-suffisance, sur YouTube) explores this topic by analyzing techniques shared on YouTube. We present Agro-STAY, a platform designed for the collection, processing, and visualization of data from YouTube videos and their comments. We use Natural Language Processing (NLP) techniques and language models, which enable a fine-grained analysis of alternative agricultural practice described online. -- Face aux crises actuelles (climatiques, sociales, \'economiques), l'auto-suffisance -- ensemble de pratiques combinant sobri\'et\'e \'energ\'etique, autoproduction alimentaire et \'energ\'etique et autoconstruction - suscite un int\'er\^et croissant. Le projet CNRS STAY (Savoirs Techniques pour l'Auto-suffisance, sur YouTube) s'inscrit dans ce domaine en analysant les savoirs techniques diffus\'es sur YouTube. Nous pr\'esentons Agro-STAY, une plateforme d\'edi\'ee \`a la collecte, au traitement et \`a la visualisation de donn\'ees issues de vid\'eos YouTube et de leurs commentaires. En mobilisant des techniques de traitement automatique des langues (TAL) et des mod\`eles de langues, ce travail permet une analyse fine des pratiques agricoles alternatives d\'ecrites en ligne.

A Quasi-Bayesian Perspective to Online Clustering

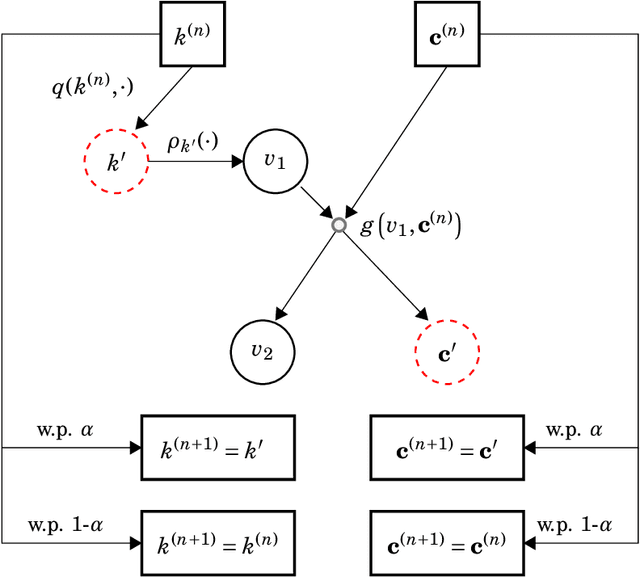
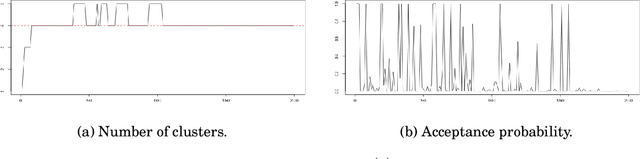
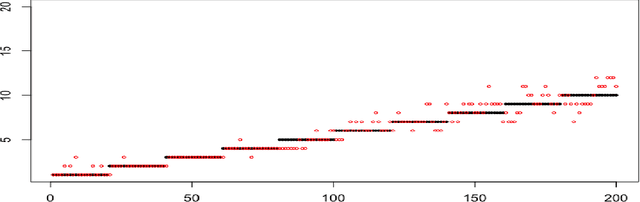
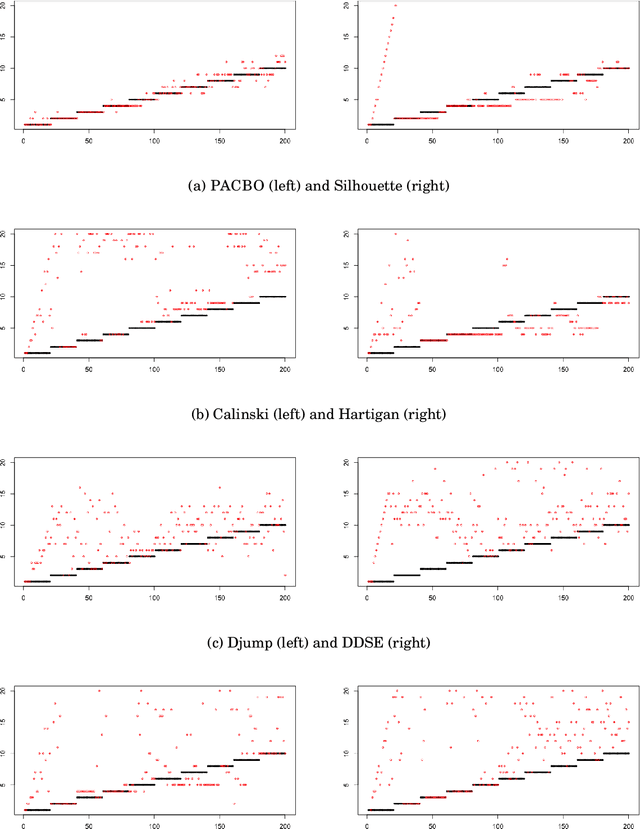
When faced with high frequency streams of data, clustering raises theoretical and algorithmic pitfalls. We introduce a new and adaptive online clustering algorithm relying on a quasi-Bayesian approach, with a dynamic (i.e., time-dependent) estimation of the (unknown and changing) number of clusters. We prove that our approach is supported by minimax regret bounds. We also provide an RJMCMC-flavored implementation (called PACBO, see https://cran.r-project.org/web/packages/PACBO/index.html) for which we give a convergence guarantee. Finally, numerical experiments illustrate the potential of our procedure.

MCMC Louvain for Online Community Detection

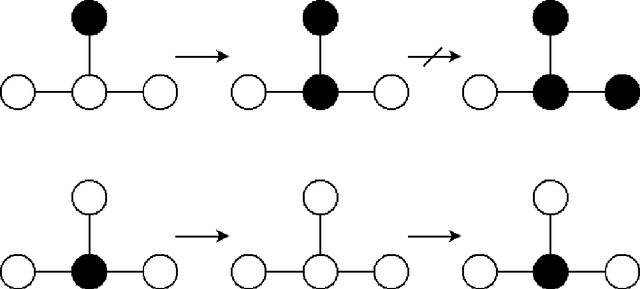
We introduce a novel algorithm of community detection that maintains dynamically a community structure of a large network that evolves with time. The algorithm maximizes the modularity index thanks to the construction of a randomized hierarchical clustering based on a Monte Carlo Markov Chain (MCMC) method. Interestingly, it could be seen as a dynamization of Louvain algorithm (see Blondel et Al, 2008) where the aggregation step is replaced by the hierarchical instrumental probability.

The algorithm of noisy k-means

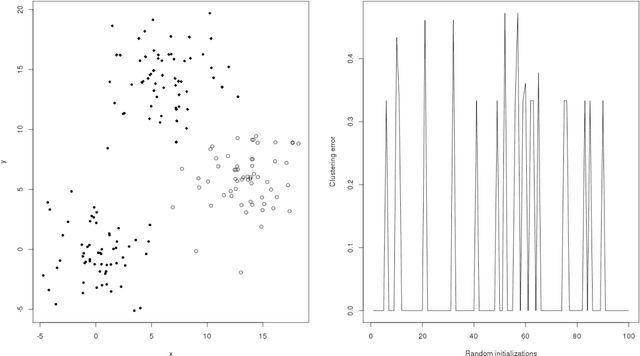
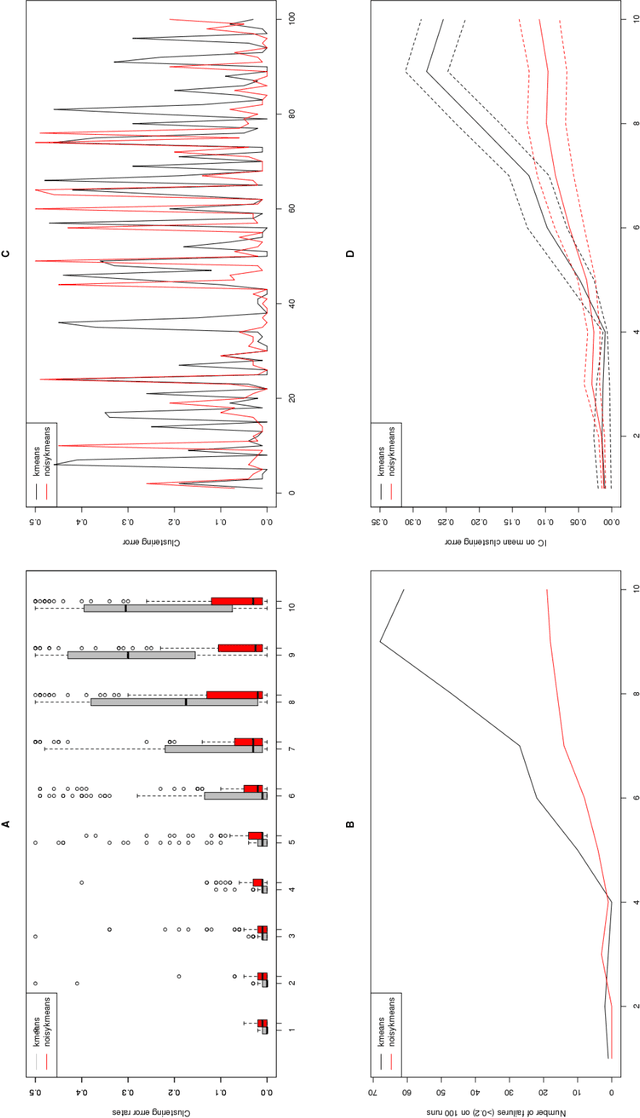
In this note, we introduce a new algorithm to deal with finite dimensional clustering with errors in variables. The design of this algorithm is based on recent theoretical advances (see Loustau (2013a,b)) in statistical learning with errors in variables. As the previous mentioned papers, the algorithm mixes different tools from the inverse problem literature and the machine learning community. Coarsely, it is based on a two-step procedure: (1) a deconvolution step to deal with noisy inputs and (2) Newton's iterations as the popular k-means.

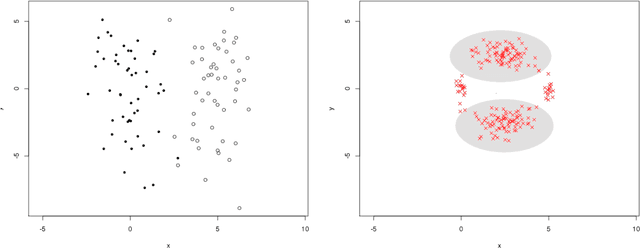
Adaptive Noisy Clustering

The problem of adaptive noisy clustering is investigated. Given a set of noisy observations $Z_i=X_i+\epsilon_i$, $i=1,...,n$, the goal is to design clusters associated with the law of $X_i$'s, with unknown density $f$ with respect to the Lebesgue measure. Since we observe a corrupted sample, a direct approach as the popular {\it $k$-means} is not suitable in this case. In this paper, we propose a noisy $k$-means minimization, which is based on the $k$-means loss function and a deconvolution estimator of the density $f$. In particular, this approach suffers from the dependence on a bandwidth involved in the deconvolution kernel. Fast rates of convergence for the excess risk are proposed for a particular choice of the bandwidth, which depends on the smoothness of the density $f$. Then, we turn out into the main issue of the paper: the data-driven choice of the bandwidth. We state an adaptive upper bound for a new selection rule, called ERC (Empirical Risk Comparison). This selection rule is based on the Lepski's principle, where empirical risks associated with different bandwidths are compared. Finally, we illustrate that this adaptive rule can be used in many statistical problems of $M$-estimation where the empirical risk depends on a nuisance parameter.

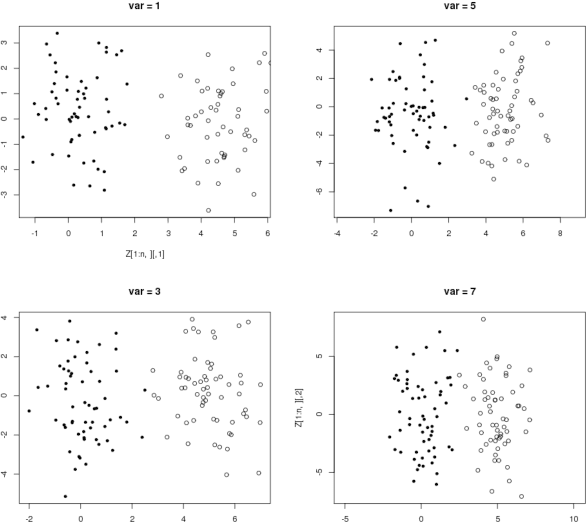
Anisotropic oracle inequalities in noisy quantization

The effect of errors in variables in quantization is investigated. We prove general exact and non-exact oracle inequalities with fast rates for an empirical minimization based on a noisy sample $Z_i=X_i+\epsilon_i,i=1,\ldots,n$, where $X_i$ are i.i.d. with density $f$ and $\epsilon_i$ are i.i.d. with density $\eta$. These rates depend on the geometry of the density $f$ and the asymptotic behaviour of the characteristic function of $\eta$. This general study can be applied to the problem of $k$-means clustering with noisy data. For this purpose, we introduce a deconvolution $k$-means stochastic minimization which reaches fast rates of convergence under standard Pollard's regularity assumptions.