Matroid Semi-Bandits in Sublinear Time

We study the matroid semi-bandits problem, where at each round the learner plays a subset of $K$ arms from a feasible set, and the goal is to maximize the expected cumulative linear rewards. Existing algorithms have per-round time complexity at least $\Omega(K)$, which becomes expensive when $K$ is large. To address this computational issue, we propose FasterCUCB whose sampling rule takes time sublinear in $K$ for common classes of matroids: $O(D\text{ polylog}(K)\text{ polylog}(T))$ for uniform matroids, partition matroids, and graphical matroids, and $O(D\sqrt{K}\text{ polylog}(T))$ for transversal matroids. Here, $D$ is the maximum number of elements in any feasible subset of arms, and $T$ is the horizon. Our technique is based on dynamic maintenance of an approximate maximum-weight basis over inner-product weights. Although the introduction of an approximate maximum-weight basis presents a challenge in regret analysis, we can still guarantee an upper bound on regret as tight as CUCB in the sense that it matches the gap-dependent lower bound by Kveton et al. (2014a) asymptotically.

Best Arm Identification with Fixed Budget: A Large Deviation Perspective

We consider the problem of identifying the best arm in stochastic Multi-Armed Bandits (MABs) using a fixed sampling budget. Characterizing the minimal instance-specific error probability for this problem constitutes one of the important remaining open problems in MABs. When arms are selected using a static sampling strategy, the error probability decays exponentially with the number of samples at a rate that can be explicitly derived via Large Deviation techniques. Analyzing the performance of algorithms with adaptive sampling strategies is however much more challenging. In this paper, we establish a connection between the Large Deviation Principle (LDP) satisfied by the empirical proportions of arm draws and that satisfied by the empirical arm rewards. This connection holds for any adaptive algorithm, and is leveraged (i) to improve error probability upper bounds of some existing algorithms, such as the celebrated \sr (Successive Rejects) algorithm \citep{audibert2010best}, and (ii) to devise and analyze new algorithms. In particular, we present \sred (Continuous Rejects), a truly adaptive algorithm that can reject arms in {\it any} round based on the observed empirical gaps between the rewards of various arms. Applying our Large Deviation results, we prove that \sred enjoys better performance guarantees than existing algorithms, including \sr. Extensive numerical experiments confirm this observation.

Improved analysis of randomized SVD for top-eigenvector approximation

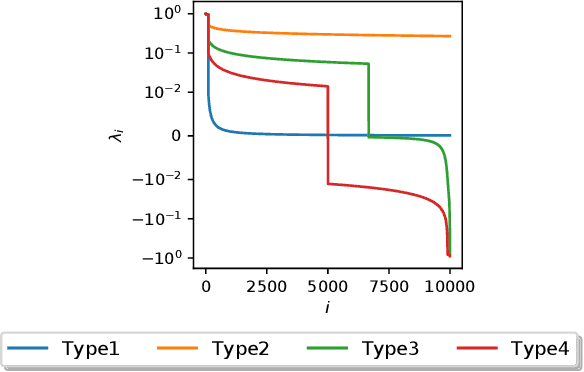
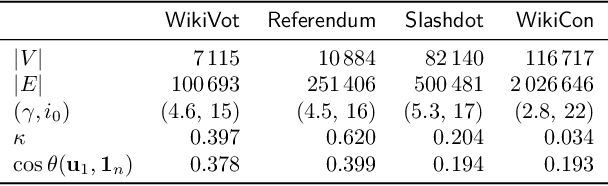
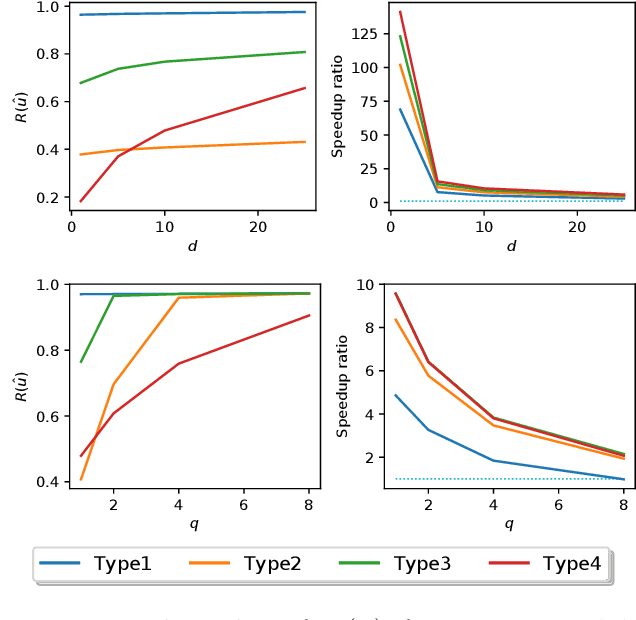
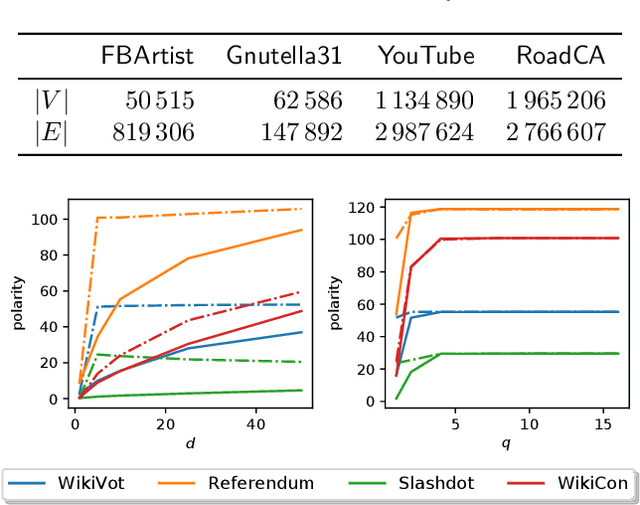
Computing the top eigenvectors of a matrix is a problem of fundamental interest to various fields. While the majority of the literature has focused on analyzing the reconstruction error of low-rank matrices associated with the retrieved eigenvectors, in many applications one is interested in finding one vector with high Rayleigh quotient. In this paper we study the problem of approximating the top-eigenvector. Given a symmetric matrix $\mathbf{A}$ with largest eigenvalue $\lambda_1$, our goal is to find a vector \hu that approximates the leading eigenvector $\mathbf{u}_1$ with high accuracy, as measured by the ratio $R(\hat{\mathbf{u}})=\lambda_1^{-1}{\hat{\mathbf{u}}^T\mathbf{A}\hat{\mathbf{u}}}/{\hat{\mathbf{u}}^T\hat{\mathbf{u}}}$. We present a novel analysis of the randomized SVD algorithm of \citet{halko2011finding} and derive tight bounds in many cases of interest. Notably, this is the first work that provides non-trivial bounds of $R(\hat{\mathbf{u}})$ for randomized SVD with any number of iterations. Our theoretical analysis is complemented with a thorough experimental study that confirms the efficiency and accuracy of the method.

Ego-CNN: Distributed, Egocentric Representations of Graphs for Detecting Critical Structures

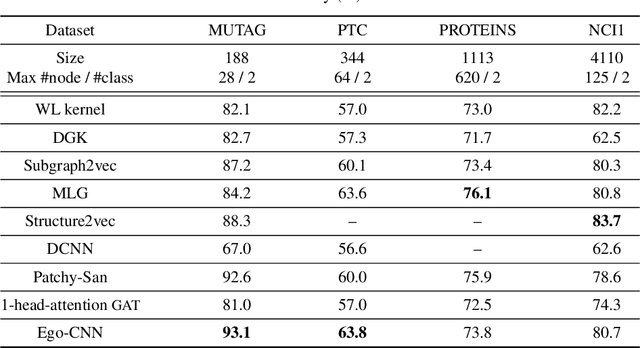
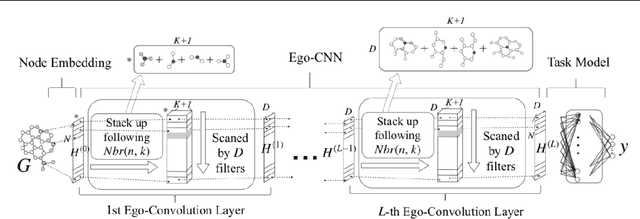
We study the problem of detecting critical structures using a graph embedding model. Existing graph embedding models lack the ability to precisely detect critical structures that are specific to a task at the global scale. In this paper, we propose a novel graph embedding model, called the Ego-CNNs, that employs the ego-convolutions convolutions at each layer and stacks up layers using an ego-centric way to detects precise critical structures efficiently. An Ego-CNN can be jointly trained with a task model and help explain/discover knowledge for the task. We conduct extensive experiments and the results show that Ego-CNNs (1) can lead to comparable task performance as the state-of-the-art graph embedding models, (2) works nicely with CNN visualization techniques to illustrate the detected structures, and (3) is efficient and can incorporate with scale-free priors, which commonly occurs in social network datasets, to further improve the training efficiency.