Policy Testing in Markov Decision Processes

We study the policy testing problem in discounted Markov decision processes (MDPs) under the fixed-confidence setting. The goal is to determine whether the value of a given policy exceeds a specified threshold while minimizing the number of observations. We begin by deriving an instance-specific lower bound that any algorithm must satisfy. This lower bound is characterized as the solution to an optimization problem with non-convex constraints. We propose a policy testing algorithm inspired by this optimization problem--a common approach in pure exploration problems such as best-arm identification, where asymptotically optimal algorithms often stem from such optimization-based characterizations. As for other pure exploration tasks in MDPs, however, the non-convex constraints in the lower-bound problem present significant challenges, raising doubts about whether statistically optimal and computationally tractable algorithms can be designed. To address this, we reformulate the lower-bound problem by interchanging the roles of the objective and the constraints, yielding an alternative problem with a non-convex objective but convex constraints. Strikingly, this reformulated problem admits an interpretation as a policy optimization task in a newly constructed reversed MDP. Leveraging recent advances in policy gradient methods, we efficiently solve this problem and use it to design a policy testing algorithm that is statistically optimal--matching the instance-specific lower bound on sample complexity--while remaining computationally tractable. We validate our approach with numerical experiments.

Best Arm Identification with Fixed Budget: A Large Deviation Perspective

We consider the problem of identifying the best arm in stochastic Multi-Armed Bandits (MABs) using a fixed sampling budget. Characterizing the minimal instance-specific error probability for this problem constitutes one of the important remaining open problems in MABs. When arms are selected using a static sampling strategy, the error probability decays exponentially with the number of samples at a rate that can be explicitly derived via Large Deviation techniques. Analyzing the performance of algorithms with adaptive sampling strategies is however much more challenging. In this paper, we establish a connection between the Large Deviation Principle (LDP) satisfied by the empirical proportions of arm draws and that satisfied by the empirical arm rewards. This connection holds for any adaptive algorithm, and is leveraged (i) to improve error probability upper bounds of some existing algorithms, such as the celebrated \sr (Successive Rejects) algorithm \citep{audibert2010best}, and (ii) to devise and analyze new algorithms. In particular, we present \sred (Continuous Rejects), a truly adaptive algorithm that can reject arms in {\it any} round based on the observed empirical gaps between the rewards of various arms. Applying our Large Deviation results, we prove that \sred enjoys better performance guarantees than existing algorithms, including \sr. Extensive numerical experiments confirm this observation.

On Uniformly Optimal Algorithms for Best Arm Identification in Two-Armed Bandits with Fixed Budget

We study the problem of best-arm identification with fixed budget in stochastic two-arm bandits with Bernoulli rewards. We prove that there is no algorithm that (i) performs as well as the algorithm sampling each arm equally (this algorithm is referred to as the {\it uniform sampling} algorithm) on all instances, and that (ii) strictly outperforms this algorithm on at least one instance. In short, there is no algorithm better than the uniform sampling algorithm. Towards this result, we first introduce the natural class of {\it consistent} and {\it stable} algorithms, and show that any algorithm that performs as well as the uniform sampling algorithm on all instances belongs to this class. The proof then proceeds by deriving a lower bound on the error rate satisfied by any consistent and stable algorithm, and by showing that the uniform sampling algorithm matches this lower bound. Our results provide a solution to the two open problems presented in \cite{qin2022open}.

Improved analysis of randomized SVD for top-eigenvector approximation

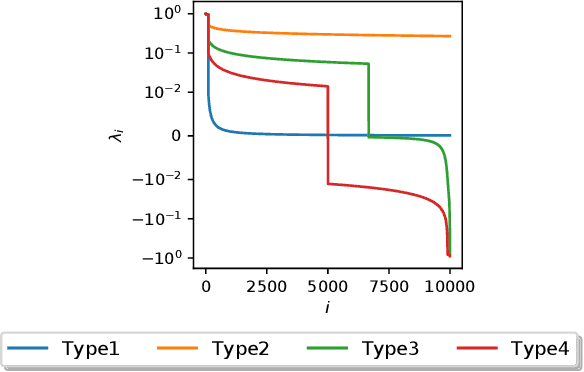
Computing the top eigenvectors of a matrix is a problem of fundamental interest to various fields. While the majority of the literature has focused on analyzing the reconstruction error of low-rank matrices associated with the retrieved eigenvectors, in many applications one is interested in finding one vector with high Rayleigh quotient. In this paper we study the problem of approximating the top-eigenvector. Given a symmetric matrix $\mathbf{A}$ with largest eigenvalue $\lambda_1$, our goal is to find a vector \hu that approximates the leading eigenvector $\mathbf{u}_1$ with high accuracy, as measured by the ratio $R(\hat{\mathbf{u}})=\lambda_1^{-1}{\hat{\mathbf{u}}^T\mathbf{A}\hat{\mathbf{u}}}/{\hat{\mathbf{u}}^T\hat{\mathbf{u}}}$. We present a novel analysis of the randomized SVD algorithm of \citet{halko2011finding} and derive tight bounds in many cases of interest. Notably, this is the first work that provides non-trivial bounds of $R(\hat{\mathbf{u}})$ for randomized SVD with any number of iterations. Our theoretical analysis is complemented with a thorough experimental study that confirms the efficiency and accuracy of the method.

An Optimal Algorithm for Multiplayer Multi-Armed Bandits

The paper addresses the Multiplayer Multi-Armed Bandit (MMAB) problem, where $M$ decision makers or players collaborate to maximize their cumulative reward. When several players select the same arm, a collision occurs and no reward is collected on this arm. Players involved in a collision are informed about this collision. We present DPE (Decentralized Parsimonious Exploration), a decentralized algorithm that achieves the same regret as that obtained by an optimal centralized algorithm. Our algorithm has better regret guarantees than the state-of-the-art algorithm SIC-MMAB \cite{boursier2019}. As in SIC-MMAB, players communicate through collisions only. An additional important advantage of DPE is that it requires very little communication. Specifically, the expected number of rounds where players use collisions to communicate is finite.