Distributed multi-agent magnetic field norm SLAM with Gaussian processes

Accurately estimating the positions of multi-agent systems in indoor environments is challenging due to the lack of Global Navigation Satelite System (GNSS) signals. Noisy measurements of position and orientation can cause the integrated position estimate to drift without bound. Previous research has proposed using magnetic field simultaneous localization and mapping (SLAM) to compensate for position drift in a single agent. Here, we propose two novel algorithms that allow multiple agents to apply magnetic field SLAM using their own and other agents measurements. Our first algorithm is a centralized approach that uses all measurements collected by all agents in a single extended Kalman filter. This algorithm simultaneously estimates the agents position and orientation and the magnetic field norm in a central unit that can communicate with all agents at all times. In cases where a central unit is not available, and there are communication drop-outs between agents, our second algorithm is a distributed approach that can be employed. We tested both algorithms by estimating the position of magnetometers carried by three people in an optical motion capture lab with simulated odometry and simulated communication dropouts between agents. We show that both algorithms are able to compensate for drift in a case where single-agent SLAM is not. We also discuss the conditions for the estimate from our distributed algorithm to converge to the estimate from the centralized algorithm, both theoretically and experimentally. Our experiments show that, for a communication drop-out rate of 80 percent, our proposed distributed algorithm, on average, provides a more accurate position estimate than single-agent SLAM. Finally, we demonstrate the drift-compensating abilities of our centralized algorithm on a real-life pedestrian localization problem with multiple agents moving inside a building.

Fast Gaussian Process Predictions on Large Geospatial Fields with Prediction-Point Dependent Basis Functions

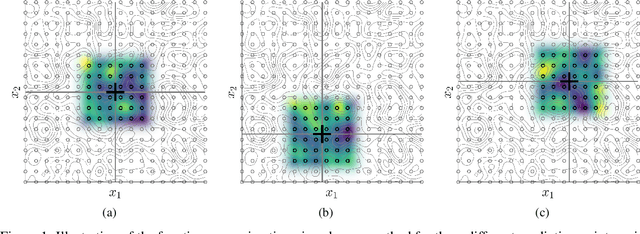
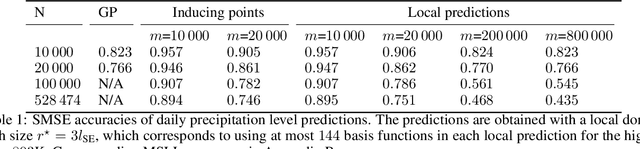
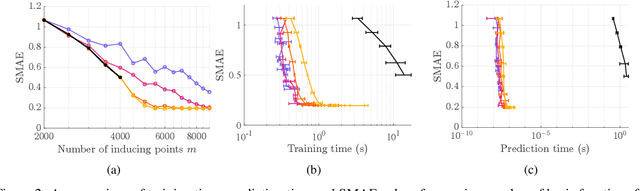
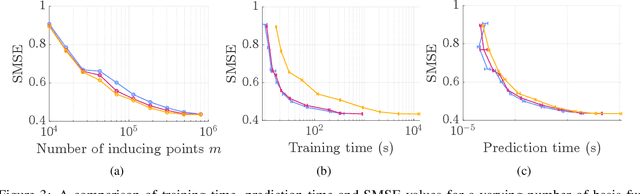
In order to perform GP predictions fast in large geospatial fields with small-scale variations, a computational complexity that is independent of the number of measurements $N$ and the size of the field is crucial. In this setting, GP approximations using $m$ basis functions requires $\mathcal{O}(Nm^2+m^3)$ computations. Using finite-support basis functions reduces the required number of computations to perform a single prediction to $\mathcal{O}(m^3)$, after a one-time training cost of $O(N)$. The prediction cost increases with increasing field size, as the number of required basis functions $m$ grows with the size of the field relative to the size of the spatial variations. To prevent the prediction speed from depending on field size, we propose leveraging the property that a subset of the trained system is a trained subset of the system to use only a local subset of $m'\ll m$ finite-support basis functions centered around each prediction point to perform predictions. Our proposed approximation requires $\mathcal{O}(m'^3)$ operations to perform each prediction after a one-time training cost of $\mathcal{O}(N)$. We show on real-life spatial data that our approach matches the prediction error of state-of-the-art methods and that it performs faster predictions, also compared to state-of-the-art approximations that lower the prediction cost of $\mathcal{O}(m^3)$ to $\mathcal{O}(m\log(m))$ using a conjugate gradient solver. Finally, we demonstrate that our approach can perform fast predictions on a global bathymetry dataset using millions of basis functions and tens of millions of measurements on a laptop computer.