Community Detection in Medical Image Datasets: Using Wavelets and Spectral Methods

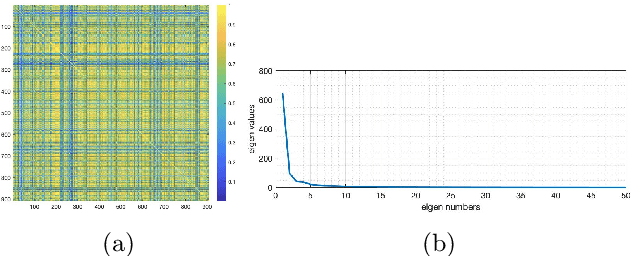
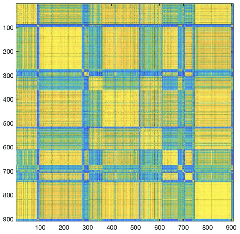
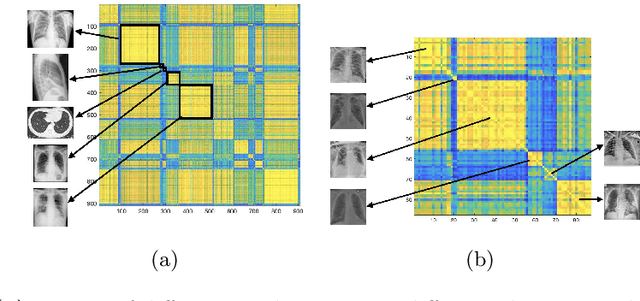
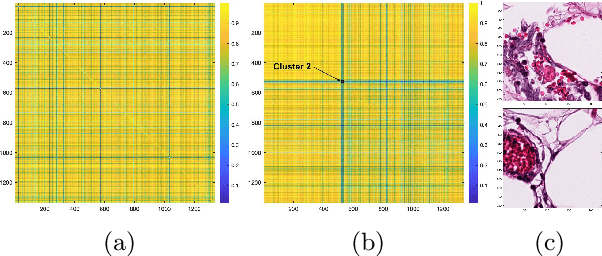
Medical image datasets can have large number of images representing patients with different health conditions and various disease severity. When dealing with raw unlabeled image datasets, the large number of samples often makes it hard for experts and non-experts to understand the variety of images present in a dataset. Supervised learning methods rely on labeled images which requires a considerable effort by medical experts to first understand the communities of images present in the data and then labeling the images. Here, we propose an algorithm to facilitate the automatic identification of communities in medical image datasets. We further explain that such analysis can also be insightful in a supervised setting, when the images are already labeled. Such insights are useful because in reality, health and disease severity can be considered a continuous spectrum, and within each class, there usually are finer communities worthy of investigation, especially when they have similarities to communities in other classes. In our approach, we use wavelet decomposition of images in tandem with spectral methods. We show that the eigenvalues of a graph Laplacian can reveal the number of notable communities in an image dataset. In our experiments, we use a dataset of images labeled with different conditions for COVID patients. We detect 25 communities in the dataset and then observe that only 6 of those communities contain patients with pneumonia. We also investigate the contents of a colorectal cancer histopathology dataset.

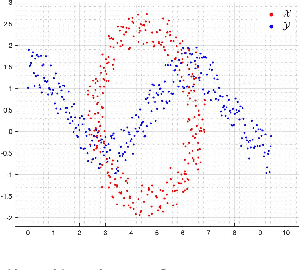
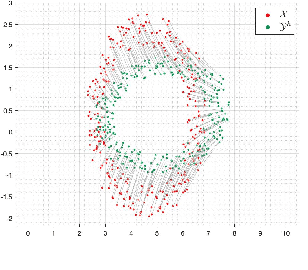
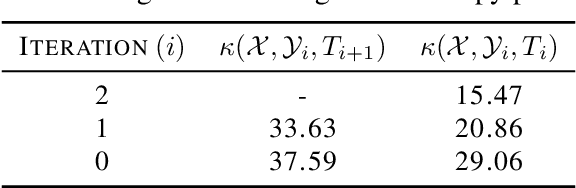
A Homotopy Algorithm for Optimal Transport

The optimal transport problem has many applications in machine learning, physics, biology, economics, etc. Although its goal is very clear and mathematically well-defined, finding its optimal solution can be challenging for large datasets in high-dimensional space. Here, we propose a homotopy algorithm that first transforms the problem into an easy form, by changing the target distribution. It then transforms the problem back to the original form through a series of iterations, tracing a path of solutions until it finds the optimal solution for the original problem. We define the homotopy path as a subspace rotation based on the orthogonal Procrustes problem, and then we discretize the homotopy path using eigenvalue decomposition of the rotation matrix. Our goal is to provide an algorithm with complexity bound $\mathcal{O}(n^2 \log(n))$, faster than the existing methods in the literature.

Extrapolation Frameworks in Cognitive Psychology Suitable for Study of Image Classification Models

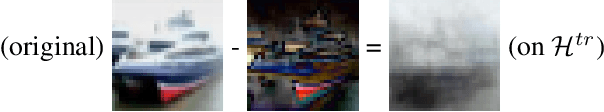
We study the functional task of deep learning image classification models and show that image classification requires extrapolation capabilities. This suggests that new theories have to be developed for the understanding of deep learning as the current theory assumes models are solely interpolating, leaving many questions about them unanswered. We investigate the pixel space and also the feature spaces extracted from images by trained models (in their hidden layers, including the 64-dimensional feature space in the last hidden layer of pre-trained residual neural networks), and also the feature space extracted by wavelets/shearlets. In all these domains, testing samples considerably fall outside the convex hull of training sets, and image classification requires extrapolation. In contrast to the deep learning literature, in cognitive science, psychology, and neuroscience, extrapolation and learning are often studied in tandem. Moreover, many aspects of human visual cognition and behavior are reported to involve extrapolation. We propose a novel extrapolation framework for the mathematical study of deep learning models. In our framework, we use the term extrapolation in this specific way of extrapolating outside the convex hull of training set (in the pixel space or feature space) but within the specific scope defined by the training data, the same way extrapolation is defined in many studies in cognitive science. We explain that our extrapolation framework can provide novel answers to open research problems about deep learning including their over-parameterization, their training regime, out-of-distribution detection, etc. We also see that the extent of extrapolation is negligible in learning tasks where deep learning is reported to have no advantage over simple models.

Federated Learning without Revealing the Decision Boundaries

We consider the recent privacy preserving methods that train the models not on original images, but on mixed images that look like noise and hard to trace back to the original images. We explain that those mixed images will be samples on the decision boundaries of the trained model, and although such methods successfully hide the contents of images from the entity in charge of federated learning, they provide crucial information to that entity about the decision boundaries of the trained model. Once the entity has exact samples on the decision boundaries of the model, they may use it for effective adversarial attacks on the model during training and/or afterwards. If we have to hide our images from that entity, how can we trust them with the decision boundaries of our model? As a remedy, we propose a method to encrypt the images, and have a decryption module hidden inside the model. The entity in charge of federated learning will only have access to a set of complex-valued coefficients, but the model will first decrypt the images and then put them through the convolutional layers. This way, the entity will not see the training images and they will not know the location of the decision boundaries of the model.

A Sketching Method for Finding the Closest Point on a Convex Hull

We develop a sketching algorithm to find the point on the convex hull of a dataset, closest to a query point outside it. Studying the convex hull of datasets can provide useful information about their geometric structure and their distribution. Many machine learning datasets have large number of samples with large number of features, but exact algorithms in computational geometry are usually not designed for such setting. Alternatively, the problem can be formulated as a linear least-squares problem with linear constraints. However, solving the problem using standard optimization algorithms can be very expensive for large datasets. Our algorithm uses a sketching procedure to exploit the structure of the data and unburden the optimization process from irrelevant points. This involves breaking the data into pieces and gradually putting the pieces back together, while improving the optimal solution using a gradient project method that can rapidly change its active set of constraints. Our method eventually leads to the optimal solution of our convex problem faster than off-the-shelf algorithms.

Deep Learning Generalization and the Convex Hull of Training Sets

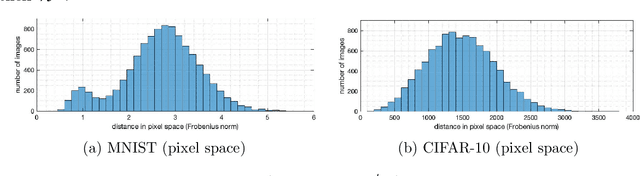
We study the generalization of deep learning models in relation to the convex hull of their training sets. A trained image classifier basically partitions its domain via decision boundaries and assigns a class to each of those partitions. The location of decision boundaries inside the convex hull of training set can be investigated in relation to the training samples. However, our analysis shows that in standard image classification datasets, all testing images are considerably outside that convex hull, in the pixel space, in the wavelet space, and in the internal representations learned by deep networks. Therefore, the performance of a trained model partially depends on how its decision boundaries are extended outside the convex hull of its training data. From this perspective which is not studied before, over-parameterization of deep learning models may be considered a necessity for shaping the extension of decision boundaries. At the same time, over-parameterization should be accompanied by a specific training regime, in order to yield a model that not only fits the training set, but also its decision boundaries extend desirably outside the convex hull. To illustrate this, we investigate the decision boundaries of a neural network, with various degrees of parameters, inside and outside the convex hull of its training set. Moreover, we use a polynomial decision boundary to study the necessity of over-parameterization and the influence of training regime in shaping its extensions outside the convex hull of training set.

Using Wavelets and Spectral Methods to Study Patterns in Image-Classification Datasets

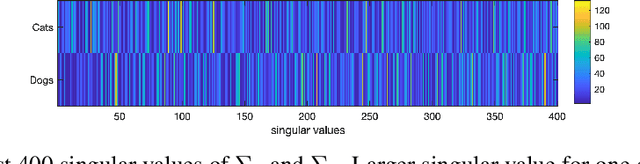
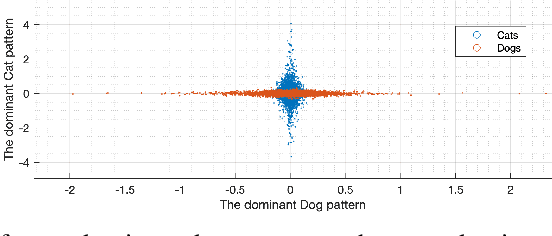
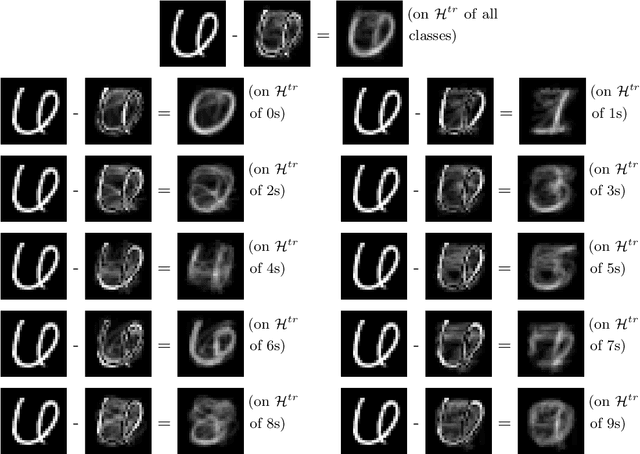
Deep learning models extract, before a final classification layer, features or patterns which are key for their unprecedented advantageous performance. However, the process of complex nonlinear feature extraction is not well understood, a major reason why interpretation, adversarial robustness, and generalization of deep neural nets are all open research problems. In this paper, we use wavelet transformation and spectral methods to analyze the contents of image classification datasets, extract specific patterns from the datasets and find the associations between patterns and classes. We show that each image can be written as the summation of a finite number of rank-1 patterns in the wavelet space, providing a low rank approximation that captures the structures and patterns essential for learning. Regarding the studies on memorization vs learning, our results clearly reveal disassociation of patterns from classes, when images are randomly labeled. Our method can be used as a pattern recognition approach to understand and interpret learnability of these datasets. It may also be used for gaining insights about the features and patterns that deep classifiers learn from the datasets.

Using wavelets to analyze similarities in image datasets

Deep learning image classifiers usually rely on huge training sets and their training process can be described as learning the similarities and differences among training images. But, images in large training sets are not usually studied from this perspective and fine-level similarities and differences among images is usually overlooked. Some studies aim to identify the influential and redundant training images, but such methods require a model that is already trained on the entire training set. Here, we show that analyzing the contents of large training sets can provide valuable insights about the classification task at hand, prior to training a model on them. We use wavelet decomposition of images and other image processing tools to perform such analysis, with no need for a pre-trained model. This makes the analysis of training sets, straightforward and fast. We show that similar images in standard datasets (such as CIFAR) can be identified in a few seconds, a significant speed-up compared to alternative methods in the literature. We also show that similarities between training and testing images may explain the generalization of models and their mistakes. Finally, we investigate the similarities between images in relation to decision boundaries of a trained model.

Auditing and Debugging Deep Learning Models via Decision Boundaries: Individual-level and Group-level Analysis

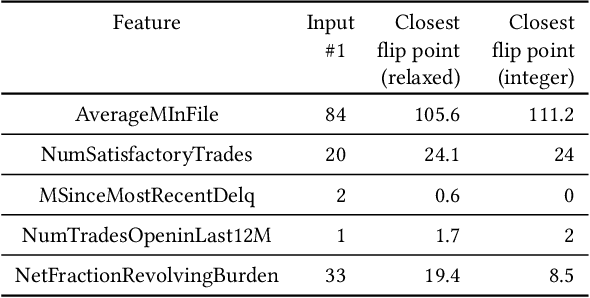
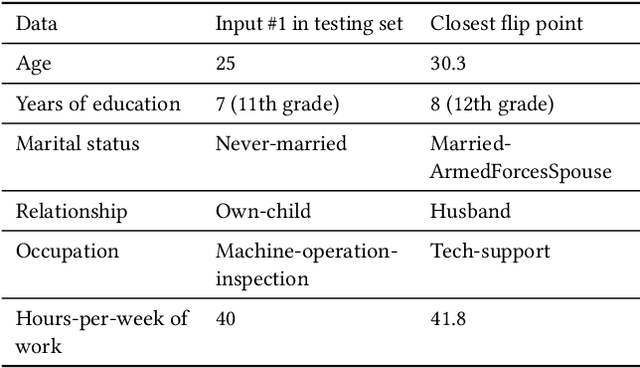
Deep learning models have been criticized for their lack of easy interpretation, which undermines confidence in their use for important applications. Nevertheless, they are consistently utilized in many applications, consequential to humans' lives, mostly because of their better performance. Therefore, there is a great need for computational methods that can explain, audit, and debug such models. Here, we use flip points to accomplish these goals for deep learning models with continuous output scores (e.g., computed by softmax), used in social applications. A flip point is any point that lies on the boundary between two output classes: e.g. for a model with a binary yes/no output, a flip point is any input that generates equal scores for "yes" and "no". The flip point closest to a given input is of particular importance because it reveals the least changes in the input that would change a model's classification, and we show that it is the solution to a well-posed optimization problem. Flip points also enable us to systematically study the decision boundaries of a deep learning classifier. The resulting insight into the decision boundaries of a deep model can clearly explain the model's output on the individual-level, via an explanation report that is understandable by non-experts. We also develop a procedure to understand and audit model behavior towards groups of people. Flip points can also be used to alter the decision boundaries in order to improve undesirable behaviors. We demonstrate our methods by investigating several models trained on standard datasets used in social applications of machine learning. We also identify the features that are most responsible for particular classifications and misclassifications.

Investigating Decision Boundaries of Trained Neural Networks

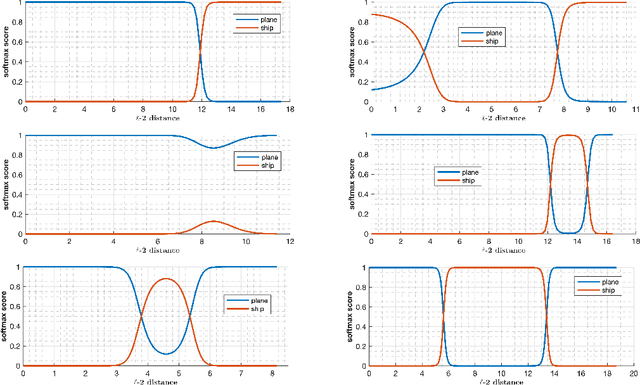
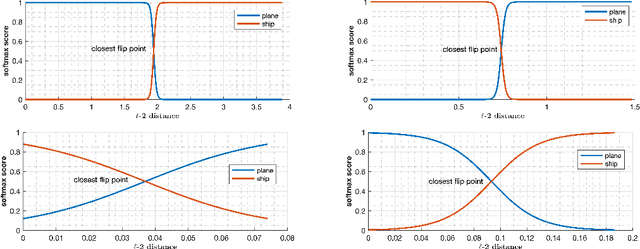
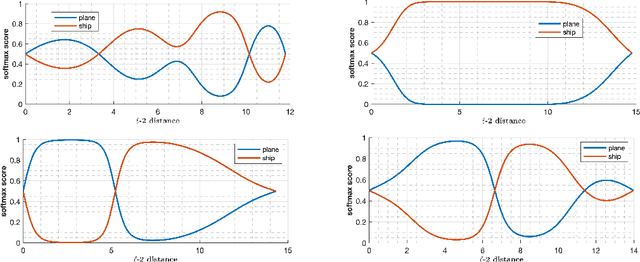
Deep learning models have been the subject of study from various perspectives, for example, their training process, interpretation, generalization error, robustness to adversarial attacks, etc. A trained model is defined by its decision boundaries, and therefore, many of the studies about deep learning models speculate about the decision boundaries, and sometimes make simplifying assumptions about them. So far, finding exact points on the decision boundaries of trained deep models has been considered an intractable problem. Here, we compute exact points on the decision boundaries of these models and provide mathematical tools to investigate the surfaces that define the decision boundaries. Through numerical results, we confirm that some of the speculations about the decision boundaries are accurate, some of the computational methods can be improved, and some of the simplifying assumptions may be unreliable, for models with nonlinear activation functions. We advocate for verification of simplifying assumptions and approximation methods, wherever they are used. Finally, we demonstrate that the computational practices used for finding adversarial examples can be improved and computing the closest point on the decision boundary reveals the weakest vulnerability of a model against adversarial attack.