Empirical Bayesian Multi-Bandit Learning

Multi-task learning in contextual bandits has attracted significant research interest due to its potential to enhance decision-making across multiple related tasks by leveraging shared structures and task-specific heterogeneity. In this article, we propose a novel hierarchical Bayesian framework for learning in various bandit instances. This framework captures both the heterogeneity and the correlations among different bandit instances through a hierarchical Bayesian model, enabling effective information sharing while accommodating instance-specific variations. Unlike previous methods that overlook the learning of the covariance structure across bandits, we introduce an empirical Bayesian approach to estimate the covariance matrix of the prior distribution.This enhances both the practicality and flexibility of learning across multi-bandits. Building on this approach, we develop two efficient algorithms: ebmTS (Empirical Bayesian Multi-Bandit Thompson Sampling) and ebmUCB (Empirical Bayesian Multi-Bandit Upper Confidence Bound), both of which incorporate the estimated prior into the decision-making process. We provide the frequentist regret upper bounds for the proposed algorithms, thereby filling a research gap in the field of multi-bandit problems. Extensive experiments on both synthetic and real-world datasets demonstrate the superior performance of our algorithms, particularly in complex environments. Our methods achieve lower cumulative regret compared to existing techniques, highlighting their effectiveness in balancing exploration and exploitation across multi-bandits.

UCB Exploration for Fixed-Budget Bayesian Best Arm Identification

We study best-arm identification (BAI) in the fixed-budget setting. Adaptive allocations based on upper confidence bounds (UCBs), such as UCBE, are known to work well in BAI. However, it is well-known that its optimal regret is theoretically dependent on instances, which we show to be an artifact in many fixed-budget BAI problems. In this paper we propose an UCB exploration algorithm that is both theoretically and empirically efficient for the fixed budget BAI problem under a Bayesian setting. The key idea is to learn prior information, which can enhance the performance of UCB-based BAI algorithm as it has done in the cumulative regret minimization problem. We establish bounds on the failure probability and the simple regret for the Bayesian BAI problem, providing upper bounds of order $\tilde{O}(\sqrt{K/n})$, up to logarithmic factors, where $n$ represents the budget and $K$ denotes the number of arms. Furthermore, we demonstrate through empirical results that our approach consistently outperforms state-of-the-art baselines.

Gradient Descent Temporal Difference-difference Learning

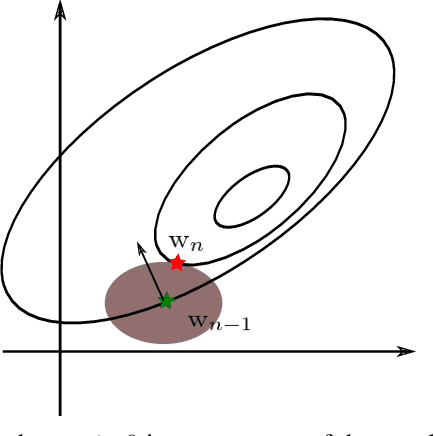
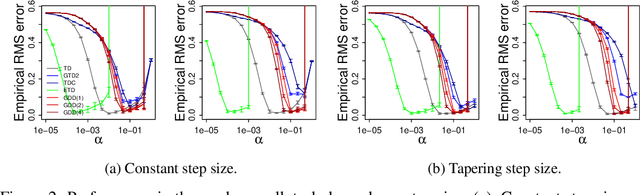
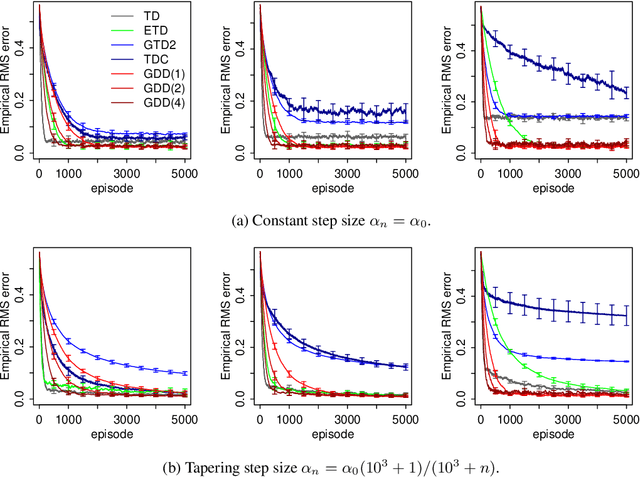
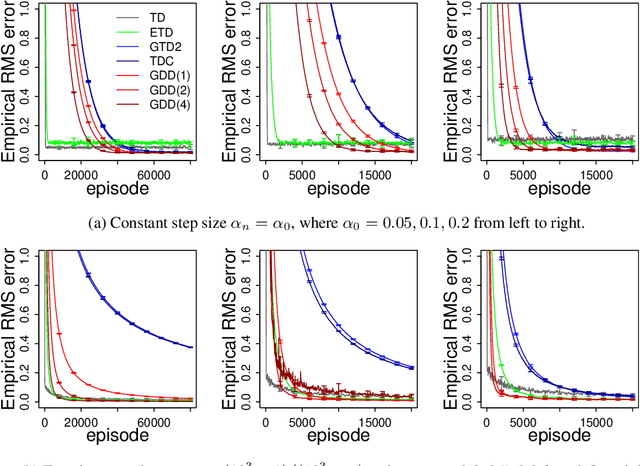
Off-policy algorithms, in which a behavior policy differs from the target policy and is used to gain experience for learning, have proven to be of great practical value in reinforcement learning. However, even for simple convex problems such as linear value function approximation, these algorithms are not guaranteed to be stable. To address this, alternative algorithms that are provably convergent in such cases have been introduced, the most well known being gradient descent temporal difference (GTD) learning. This algorithm and others like it, however, tend to converge much more slowly than conventional temporal difference learning. In this paper we propose gradient descent temporal difference-difference (Gradient-DD) learning in order to improve GTD2, a GTD algorithm, by introducing second-order differences in successive parameter updates. We investigate this algorithm in the framework of linear value function approximation, theoretically proving its convergence by applying the theory of stochastic approximation. %analytically showing its improvement over GTD2. Studying the model empirically on the random walk task, the Boyan-chain task, and the Baird's off-policy counterexample, we find substantial improvement over GTD2 and, in several cases, better performance even than conventional TD learning.