Neural Fields for Fast and Scalable Interpolation of Geophysical Ocean Variables

Optimal Interpolation (OI) is a widely used, highly trusted algorithm for interpolation and reconstruction problems in geosciences. With the influx of more satellite missions, we have access to more and more observations and it is becoming more pertinent to take advantage of these observations in applications such as forecasting and reanalysis. With the increase in the volume of available data, scalability remains an issue for standard OI and it prevents many practitioners from effectively and efficiently taking advantage of these large sums of data to learn the model hyperparameters. In this work, we leverage recent advances in Neural Fields (NerFs) as an alternative to the OI framework where we show how they can be easily applied to standard reconstruction problems in physical oceanography. We illustrate the relevance of NerFs for gap-filling of sparse measurements of sea surface height (SSH) via satellite altimetry and demonstrate how NerFs are scalable with comparable results to the standard OI. We find that NerFs are a practical set of methods that can be readily applied to geoscience interpolation problems and we anticipate a wider adoption in the future.

Deep learning for Lagrangian drift simulation at the sea surface

We address Lagrangian drift simulation in geophysical dynamics and explore deep learning approaches to overcome known limitations of state-of-the-art model-based and Markovian approaches in terms of computational complexity and error propagation. We introduce a novel architecture, referred to as DriftNet, inspired from the Eulerian Fokker-Planck representation of Lagrangian dynamics. Numerical experiments for Lagrangian drift simulation at the sea surface demonstrates the relevance of DriftNet w.r.t. state-of-the-art schemes. Benefiting from the fully-convolutional nature of Drift-Net, we explore through a neural inversion how to diagnose modelderived velocities w.r.t. real drifter trajectories.

Learning Neural Optimal Interpolation Models and Solvers

The reconstruction of gap-free signals from observation data is a critical challenge for numerous application domains, such as geoscience and space-based earth observation, when the available sensors or the data collection processes lead to irregularly-sampled and noisy observations. Optimal interpolation (OI), also referred to as kriging, provides a theoretical framework to solve interpolation problems for Gaussian processes (GP). The associated computational complexity being rapidly intractable for n-dimensional tensors and increasing numbers of observations, a rich literature has emerged to address this issue using ensemble methods, sparse schemes or iterative approaches. Here, we introduce a neural OI scheme. It exploits a variational formulation with convolutional auto-encoders and a trainable iterative gradient-based solver. Theoretically equivalent to the OI formulation, the trainable solver asymptotically converges to the OI solution when dealing with both stationary and non-stationary linear spatio-temporal GPs. Through a bi-level optimization formulation, we relate the learning step and the selection of the training loss to the theoretical properties of the OI, which is an unbiased estimator with minimal error variance. Numerical experiments for 2D+t synthetic GP datasets demonstrate the relevance of the proposed scheme to learn computationally-efficient and scalable OI models and solvers from data. As illustrated for a real-world interpolation problems for satellite-derived geophysical dynamics, the proposed framework also extends to non-linear and multimodal interpolation problems and significantly outperforms state-of-the-art interpolation methods, when dealing with very high missing data rates.

4DVarNet-SSH: end-to-end learning of variational interpolation schemes for nadir and wide-swath satellite altimetry

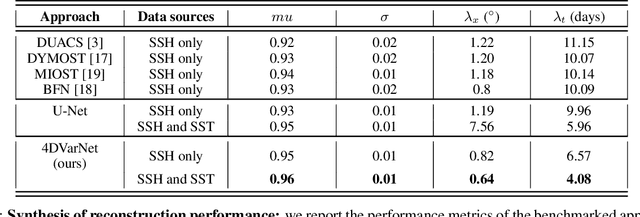
The reconstruction of sea surface currents from satellite altimeter data is a key challenge in spatial oceanography, especially with the upcoming wide-swath SWOT (Surface Ocean and Water Topography) altimeter mission. Operational systems however generally fail to retrieve mesoscale dynamics for horizontal scales below 100km and time-scale below 10 days. Here, we address this challenge through the 4DVarnet framework, an end-to-end neural scheme backed on a variational data assimilation formulation. We introduce a parametrization of the 4DVarNet scheme dedicated to the space-time interpolation of satellite altimeter data. Within an observing system simulation experiment (NATL60), we demonstrate the relevance of the proposed approach both for nadir and nadir+swot altimeter configurations for two contrasted case-study regions in terms of upper ocean dynamics. We report relative improvement with respect to the operational optimal interpolation between 30% and 60% in terms of reconstruction error. Interestingly, for the nadir+swot altimeter configuration, we reach resolved space-time scales below 70km and 7days. The code is open-source to enable reproductibility and future collaborative developments. Beyond its applicability to large-scale domains, we also address uncertainty quantification issues and generalization properties of the proposed learning setting. We discuss further future research avenues and extensions to other ocean data assimilation and space oceanography challenges.

Learning-based estimation of in-situ wind speed from underwater acoustics

Wind speed retrieval at sea surface is of primary importance for scientific and operational applications. Besides weather models, in-situ measurements and remote sensing technologies, especially satellite sensors, provide complementary means to monitor wind speed. As sea surface winds produce sounds that propagate underwater, underwater acoustics recordings can also deliver fine-grained wind-related information. Whereas model-driven schemes, especially data assimilation approaches, are the state-of-the-art schemes to address inverse problems in geoscience, machine learning techniques become more and more appealing to fully exploit the potential of observation datasets. Here, we introduce a deep learning approach for the retrieval of wind speed time series from underwater acoustics possibly complemented by other data sources such as weather model reanalyses. Our approach bridges data assimilation and learning-based frameworks to benefit both from prior physical knowledge and computational efficiency. Numerical experiments on real data demonstrate that we outperform the state-of-the-art data-driven methods with a relative gain up to 16% in terms of RMSE. Interestingly, these results support the relevance of the time dynamics of underwater acoustic data to better inform the time evolution of wind speed. They also show that multimodal data, here underwater acoustics data combined with ECMWF reanalysis data, may further improve the reconstruction performance, including the robustness with respect to missing underwater acoustics data.

Rain Rate Estimation with SAR using NEXRAD measurements with Convolutional Neural Networks

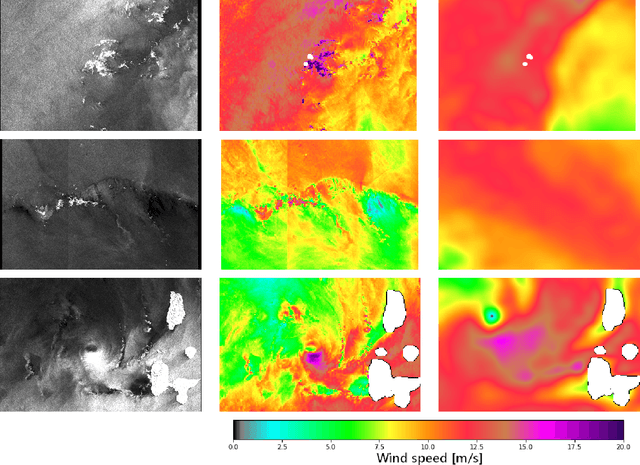
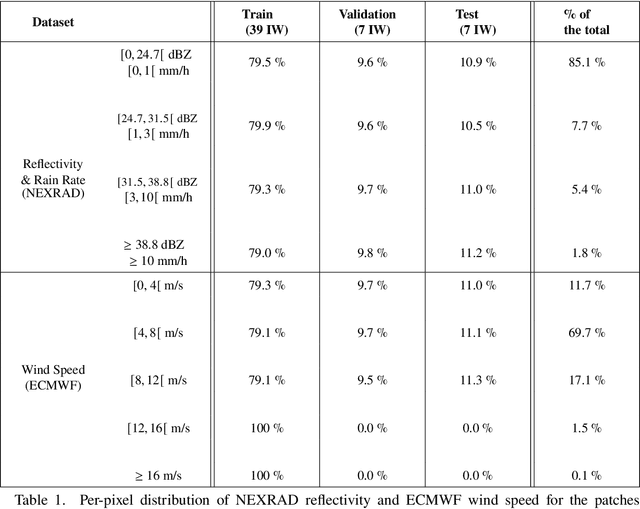
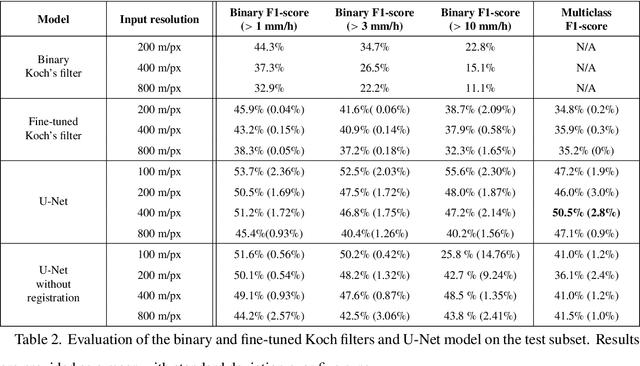
Remote sensing of rainfall events is critical for both operational and scientific needs, including for example weather forecasting, extreme flood mitigation, water cycle monitoring, etc. Ground-based weather radars, such as NOAA's Next-Generation Radar (NEXRAD), provide reflectivity and precipitation measurements of rainfall events. However, the observation range of such radars is limited to a few hundred kilometers, prompting the exploration of other remote sensing methods, paricularly over the open ocean, that represents large areas not covered by land-based radars. For a number of decades, C-band SAR imagery such a such as Sentinel-1 imagery has been known to exhibit rainfall signatures over the sea surface. However, the development of SAR-derived rainfall products remains a challenge. Here we propose a deep learning approach to extract rainfall information from SAR imagery. We demonstrate that a convolutional neural network, such as U-Net, trained on a colocated and preprocessed Sentinel-1/NEXRAD dataset clearly outperforms state-of-the-art filtering schemes. Our results indicate high performance in segmenting precipitation regimes, delineated by thresholds at 1, 3, and 10 mm/h. Compared to current methods that rely on Koch filters to draw binary rainfall maps, these multi-threshold learning-based models can provide rainfall estimation for higher wind speeds and thus may be of great interest for data assimilation weather forecasting or for improving the qualification of SAR-derived wind field data.

Multimodal 4DVarNets for the reconstruction of sea surface dynamics from SST-SSH synergies

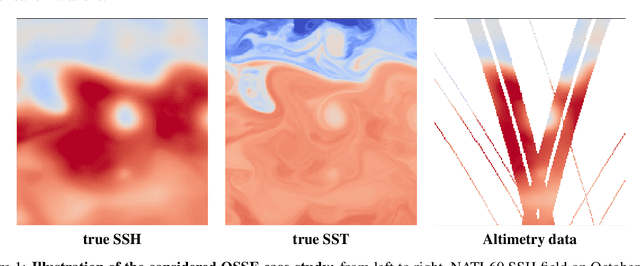
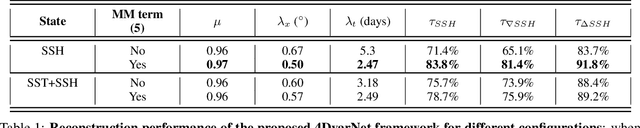
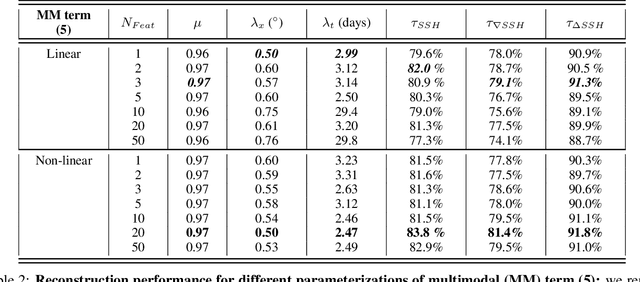
Due to the irregular space-time sampling of sea surface observations, the reconstruction of sea surface dynamics is a challenging inverse problem. While satellite altimetry provides a direct observation of the sea surface height (SSH), which relates to the divergence-free component of sea surface currents, the associated sampling pattern prevents from retrieving fine-scale sea surface dynamics, typically below a 10-day time scale. By contrast, other satellite sensors provide higher-resolution observations of sea surface tracers such as sea surface temperature (SST). Multimodal inversion schemes then arise as an appealing strategy. Though theoretical evidence supports the existence of an explicit relationship between sea surface temperature and sea surface dynamics under specific dynamical regimes, the generalization to the variety of upper ocean dynamical regimes is complex. Here, we investigate this issue from a physics-informed learning perspective. We introduce a trainable multimodal inversion scheme for the reconstruction of sea surface dynamics from multi-source satellite-derived observations. The proposed 4DVarNet schemes combine a variational formulation involving trainable observation and a priori terms with a trainable gradient-based solver. We report an application to the reconstruction of the divergence-free component of sea surface dynamics from satellite-derived SSH and SST data. An observing system simulation experiment for a Gulf Stream region supports the relevance of our approach compared with state-of-the-art schemes. We report relative improvement greater than 50% compared with the operational altimetry product in terms of root mean square error and resolved space-time scales. We discuss further the application and extension of the proposed approach for the reconstruction and forecasting of geophysical dynamics from irregularly-sampled satellite observations.

A posteriori learning for quasi-geostrophic turbulence parametrization

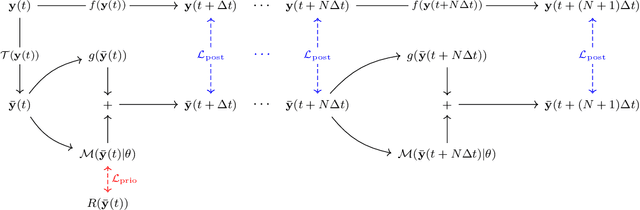
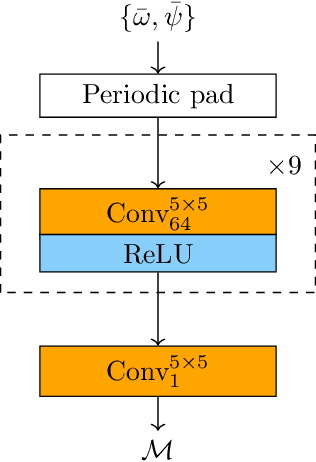
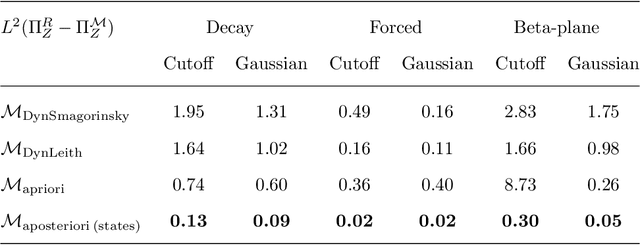
The use of machine learning to build subgrid parametrizations for climate models is receiving growing attention. State-of-the-art strategies address the problem as a supervised learning task and optimize algorithms that predict subgrid fluxes based on information from coarse resolution models. In practice, training data are generated from higher resolution numerical simulations transformed in order to mimic coarse resolution simulations. By essence, these strategies optimize subgrid parametrizations to meet so-called $\textit{a priori}$ criteria. But the actual purpose of a subgrid parametrization is to obtain good performance in terms of $\textit{a posteriori}$ metrics which imply computing entire model trajectories. In this paper, we focus on the representation of energy backscatter in two dimensional quasi-geostrophic turbulence and compare parametrizations obtained with different learning strategies at fixed computational complexity. We show that strategies based on $\textit{a priori}$ criteria yield parametrizations that tend to be unstable in direct simulations and describe how subgrid parametrizations can alternatively be trained end-to-end in order to meet $\textit{a posteriori}$ criteria. We illustrate that end-to-end learning strategies yield parametrizations that outperform known empirical and data-driven schemes in terms of performance, stability and ability to apply to different flow configurations. These results support the relevance of differentiable programming paradigms for climate models in the future.

Multimodal learning-based inversion models for the space-time reconstruction of satellite-derived geophysical fields

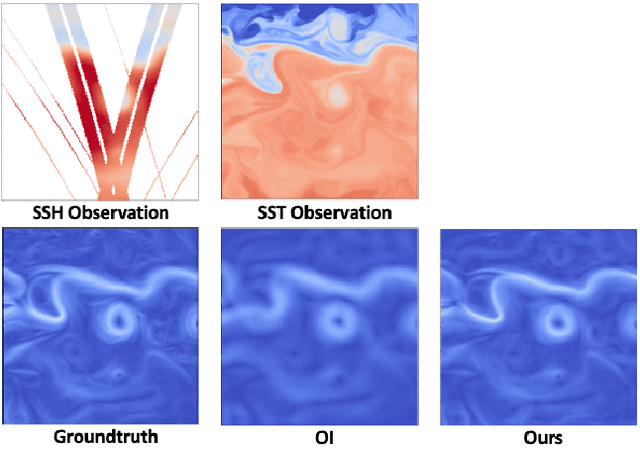
For numerous earth observation applications, one may benefit from various satellite sensors to address the reconstruction of some process or information of interest. A variety of satellite sensors deliver observation data with different sampling patterns due satellite orbits and/or their sensitivity to atmospheric conditions (e.g., clour cover, heavy rains,...). Beyond the ability to account for irregularly-sampled observations, the definition of model-driven inversion methods is often limited to specific case-studies where one can explicitly derive a physical model to relate the different observation sources. Here, we investigate how end-to-end learning schemes provide new means to address multimodal inversion problems. The proposed scheme combines a variational formulation with trainable observation operators, {\em a priori} terms and solvers. Through an application to space oceanography, we show how this scheme can successfully extract relevant information from satellite-derived sea surface temperature images and enhance the reconstruction of sea surface currents issued from satellite altimetry data.

Bounded nonlinear forecasts of partially observed geophysical systems with physics-constrained deep learning

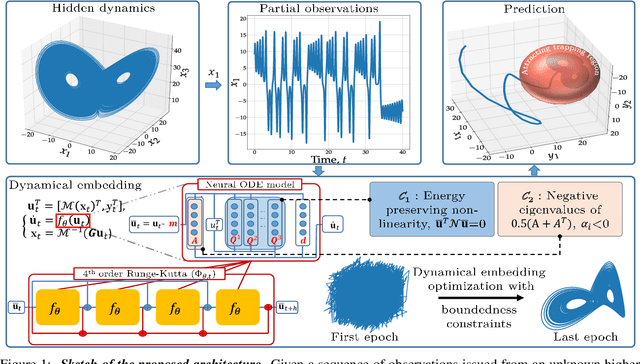
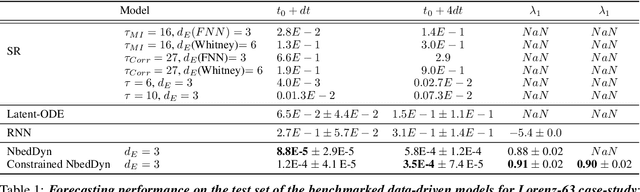
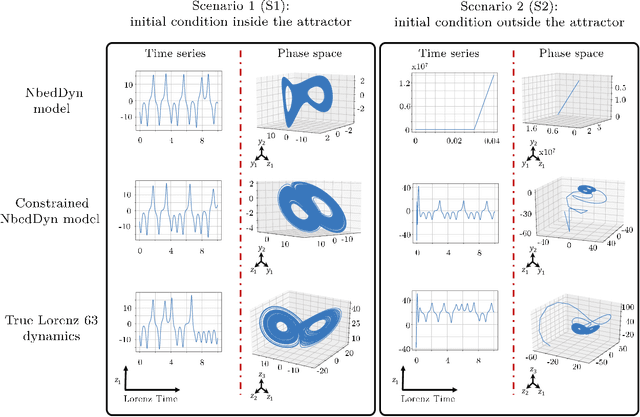
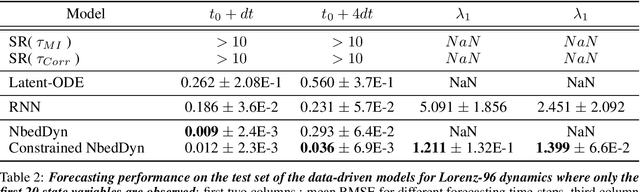
The complexity of real-world geophysical systems is often compounded by the fact that the observed measurements depend on hidden variables. These latent variables include unresolved small scales and/or rapidly evolving processes, partially observed couplings, or forcings in coupled systems. This is the case in ocean-atmosphere dynamics, for which unknown interior dynamics can affect surface observations. The identification of computationally-relevant representations of such partially-observed and highly nonlinear systems is thus challenging and often limited to short-term forecast applications. Here, we investigate the physics-constrained learning of implicit dynamical embeddings, leveraging neural ordinary differential equation (NODE) representations. A key objective is to constrain their boundedness, which promotes the generalization of the learned dynamics to arbitrary initial condition. The proposed architecture is implemented within a deep learning framework, and its relevance is demonstrated with respect to state-of-the-art schemes for different case-studies representative of geophysical dynamics.