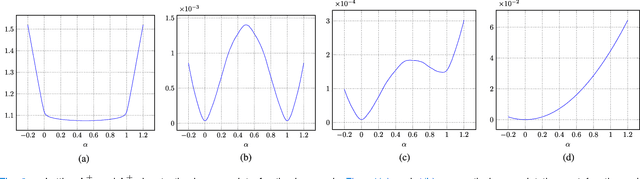
Smooth optimization algorithms for global and locally low-rank regularizers

Many inverse problems and signal processing problems involve low-rank regularizers based on the nuclear norm. Commonly, proximal gradient methods (PGM) are adopted to solve this type of non-smooth problems as they can offer fast and guaranteed convergence. However, PGM methods cannot be simply applied in settings where low-rank models are imposed locally on overlapping patches; therefore, heuristic approaches have been proposed that lack convergence guarantees. In this work we propose to replace the nuclear norm with a smooth approximation in which a Huber-type function is applied to each singular value. By providing a theoretical framework based on singular value function theory, we show that important properties can be established for the proposed regularizer, such as: convexity, differentiability, and Lipschitz continuity of the gradient. Moreover, we provide a closed-form expression for the regularizer gradient, enabling the use of standard iterative gradient-based optimization algorithms (e.g., nonlinear conjugate gradient) that can easily address the case of overlapping patches and have well-known convergence guarantees. In addition, we provide a novel step-size selection strategy based on a quadratic majorizer of the line-search function that leverages the Huber characteristics of the proposed regularizer. Finally, we assess the proposed optimization framework by providing empirical results in dynamic magnetic resonance imaging (MRI) reconstruction in the context of locally low-rank models with overlapping patches.

Extended Version of "New Theory and Faster Computations for Subspace-Based Sensitivity Map Estimation in Multichannel MRI''

This is an unabridged version of a journal manuscript that has been submitted for publication [1]. (Due to length restrictions, we were forced to remove substantial amounts of content from the version that was submitted to the journal, including more detailed theoretical explanations, additional figures, and a more comprehensive bibliography. This content remains intact in this version of the document). Sensitivity map estimation is important in many multichannel MRI applications. Subspace-based sensitivity map estimation methods like ESPIRiT are popular and perform well, though can be computationally expensive and their theoretical principles can be nontrivial to understand. In the first part of this work, we present a novel theoretical derivation of subspace-based sensitivity map estimation based on a linear-predictability/structured low-rank modeling perspective. This results in an estimation approach that is equivalent to ESPIRiT, but with distinct theory that may be more intuitive for some readers. In the second part of this work, we propose and evaluate a set of computational acceleration approaches (collectively known as PISCO) that can enable substantial improvements in computation time (up to ~100x in the examples we show) and memory for subspace-based sensitivity map estimation.

Robust Autocalibrated Structured Low-Rank EPI Ghost Correction

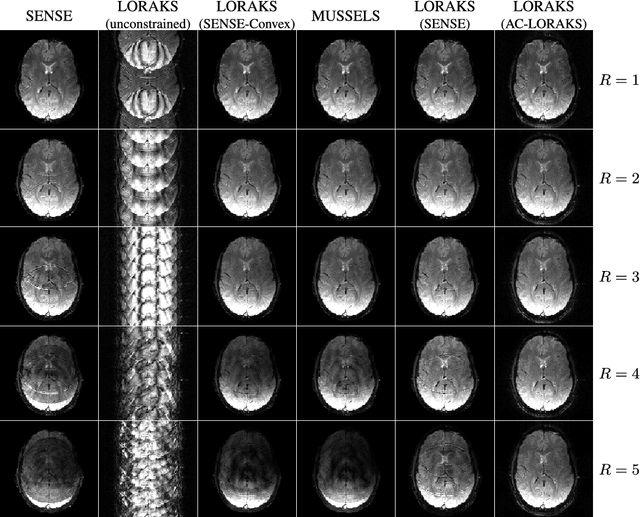
Purpose: We propose and evaluate a new structured low-rank method for EPI ghost correction called Robust Autocalibrated LORAKS (RAC-LORAKS). The method can be used to suppress EPI ghosts arising from the differences between different readout gradient polarities and/or the differences between different shots. It does not require conventional EPI navigator signals, and is robust to imperfect autocalibration data. Methods: Autocalibrated LORAKS is a previous structured low-rank method for EPI ghost correction that uses GRAPPA-type autocalibration data to enable high-quality ghost correction. This method works well when the autocalibration data is pristine, but performance degrades substantially when the autocalibration information is imperfect. RAC-LORAKS generalizes Autocalibrated LORAKS in two ways. First, it does not completely trust the information from autocalibration data, and instead considers the autocalibration and EPI data simultaneously when estimating low-rank matrix structure. And second, it uses complementary information from the autocalibration data to improve EPI reconstruction in a multi-contrast joint reconstruction framework. RAC-LORAKS is evaluated using simulations and in vivo data, and compared to state-of-the-art methods. Results: RAC-LORAKS is demonstrated to have good ghost elimination performance compared to state-of-the-art methods in several complicated acquisition scenarios (including gradient-echo brain imaging, diffusion-encoded brain imaging, and cardiac imaging). Conclusion: RAC-LORAKS provides effective suppression of EPI ghosts and is robust to imperfect autocalibration data.

Navigator-free EPI Ghost Correction with Structured Low-Rank Matrix Models: New Theory and Methods

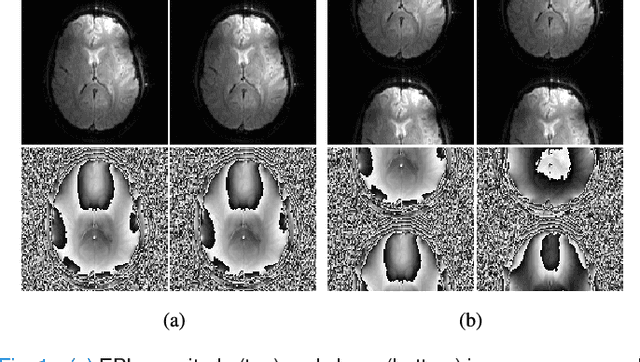
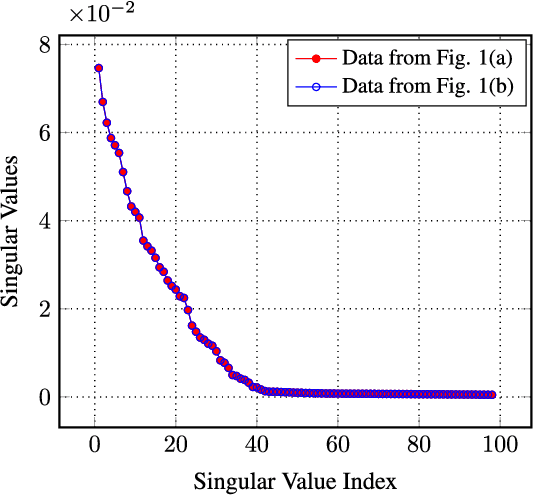
Structured low-rank matrix models have previously been introduced to enable calibrationless MR image reconstruction from sub-Nyquist data, and such ideas have recently been extended to enable navigator-free echo-planar imaging (EPI) ghost correction. This paper presents novel theoretical analysis which shows that, because of uniform subsampling, the structured low-rank matrix optimization problems for EPI data will always have either undesirable or non-unique solutions in the absence of additional constraints. This theory leads us to recommend and investigate problem formulations for navigator-free EPI that incorporate side information from either image-domain or k-space domain parallel imaging methods. The importance of using nonconvex low-rank matrix regularization is also identified. We demonstrate using phantom and \emph{in vivo} data that the proposed methods are able to eliminate ghost artifacts for several navigator-free EPI acquisition schemes, obtaining better performance in comparison to state-of-the-art methods across a range of different scenarios. Results are shown for both single-channel acquisition and highly accelerated multi-channel acquisition.