Unified Brain Surface and Volume Registration

Accurate registration of brain MRI scans is fundamental for cross-subject analysis in neuroscientific studies. This involves aligning both the cortical surface of the brain and the interior volume. Traditional methods treat volumetric and surface-based registration separately, which often leads to inconsistencies that limit downstream analyses. We propose a deep learning framework, NeurAlign, that registers $3$D brain MRI images by jointly aligning both cortical and subcortical regions through a unified volume-and-surface-based representation. Our approach leverages an intermediate spherical coordinate space to bridge anatomical surface topology with volumetric anatomy, enabling consistent and anatomically accurate alignment. By integrating spherical registration into the learning, our method ensures geometric coherence between volume and surface domains. In a series of experiments on both in-domain and out-of-domain datasets, our method consistently outperforms both classical and machine learning-based registration methods -- improving the Dice score by up to 7 points while maintaining regular deformation fields. Additionally, it is orders of magnitude faster than the standard method for this task, and is simpler to use because it requires no additional inputs beyond an MRI scan. With its superior accuracy, fast inference, and ease of use, NeurAlign sets a new standard for joint cortical and subcortical registration.

Normalizing Diffusion Kernels with Optimal Transport

Smoothing a signal based on local neighborhoods is a core operation in machine learning and geometry processing. On well-structured domains such as vector spaces and manifolds, the Laplace operator derived from differential geometry offers a principled approach to smoothing via heat diffusion, with strong theoretical guarantees. However, constructing such Laplacians requires a carefully defined domain structure, which is not always available. Most practitioners thus rely on simple convolution kernels and message-passing layers, which are biased against the boundaries of the domain. We bridge this gap by introducing a broad class of smoothing operators, derived from general similarity or adjacency matrices, and demonstrate that they can be normalized into diffusion-like operators that inherit desirable properties from Laplacians. Our approach relies on a symmetric variant of the Sinkhorn algorithm, which rescales positive smoothing operators to match the structural behavior of heat diffusion. This construction enables Laplacian-like smoothing and processing of irregular data such as point clouds, sparse voxel grids or mixture of Gaussians. We show that the resulting operators not only approximate heat diffusion but also retain spectral information from the Laplacian itself, with applications to shape analysis and matching.

Memory-Scalable and Simplified Functional Map Learning

Deep functional maps have emerged in recent years as a prominent learning-based framework for non-rigid shape matching problems. While early methods in this domain only focused on learning in the functional domain, the latest techniques have demonstrated that by promoting consistency between functional and pointwise maps leads to significant improvements in accuracy. Unfortunately, existing approaches rely heavily on the computation of large dense matrices arising from soft pointwise maps, which compromises their efficiency and scalability. To address this limitation, we introduce a novel memory-scalable and efficient functional map learning pipeline. By leveraging the specific structure of functional maps, we offer the possibility to achieve identical results without ever storing the pointwise map in memory. Furthermore, based on the same approach, we present a differentiable map refinement layer adapted from an existing axiomatic refinement algorithm. Unlike many functional map learning methods, which use this algorithm at a post-processing step, ours can be easily used at train time, enabling to enforce consistency between the refined and initial versions of the map. Our resulting approach is both simpler, more efficient and more numerically stable, by avoiding differentiation through a linear system, while achieving close to state-of-the-art results in challenging scenarios.

Smooth Non-Rigid Shape Matching via Effective Dirichlet Energy Optimization

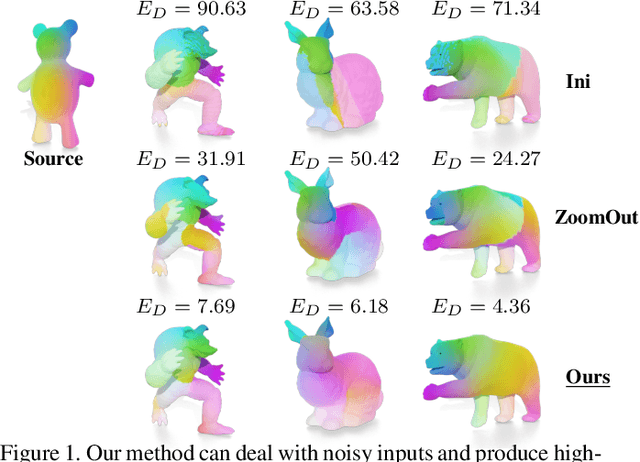
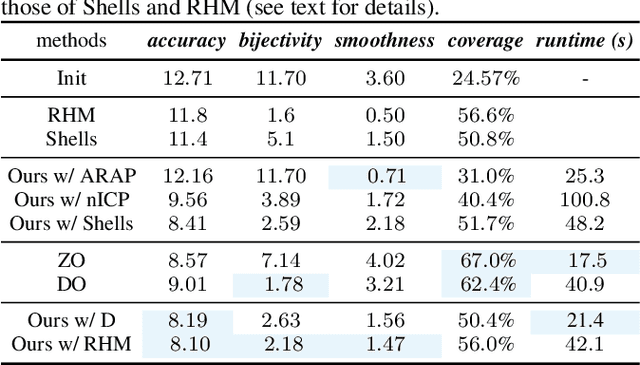
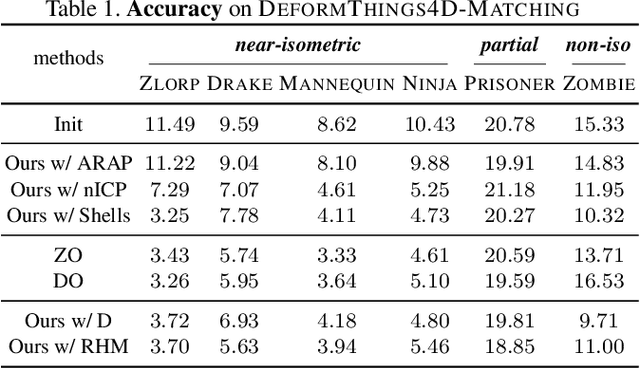
We introduce pointwise map smoothness via the Dirichlet energy into the functional map pipeline, and propose an algorithm for optimizing it efficiently, which leads to high-quality results in challenging settings. Specifically, we first formulate the Dirichlet energy of the pulled-back shape coordinates, as a way to evaluate smoothness of a pointwise map across discrete surfaces. We then extend the recently proposed discrete solver and show how a strategy based on auxiliary variable reformulation allows us to optimize pointwise map smoothness alongside desirable functional map properties such as bijectivity. This leads to an efficient map refinement strategy that simultaneously improves functional and point-to-point correspondences, obtaining smooth maps even on non-isometric shape pairs. Moreover, we demonstrate that several previously proposed methods for computing smooth maps can be reformulated as variants of our approach, which allows us to compare different formulations in a consistent framework. Finally, we compare these methods both on existing benchmarks and on a new rich dataset that we introduce, which contains non-rigid, non-isometric shape pairs with inter-category and cross-category correspondences. Our work leads to a general framework for optimizing and analyzing map smoothness both conceptually and in challenging practical settings.