Adaptive Off-Policy Inference for M-Estimators Under Model Misspecification

When data are collected adaptively, such as in bandit algorithms, classical statistical approaches such as ordinary least squares and $M$-estimation will often fail to achieve asymptotic normality. Although recent lines of work have modified the classical approaches to ensure valid inference on adaptively collected data, most of these works assume that the model is correctly specified. We propose a method that provides valid inference for M-estimators that use adaptively collected bandit data with a (possibly) misspecified working model. A key ingredient in our approach is the use of flexible machine learning approaches to stabilize the variance induced by adaptive data collection. A major novelty is that our procedure enables the construction of valid confidence sets even in settings where treatment policies are unstable and non-converging, such as when there is no unique optimal arm and standard bandit algorithms are used. Empirical results on semi-synthetic datasets constructed from the Osteoarthritis Initiative demonstrate that the method maintains type I error control, while existing methods for inference in adaptive settings do not cover in the misspecified case.

Universal Inference Meets Random Projections: A Scalable Test for Log-concavity

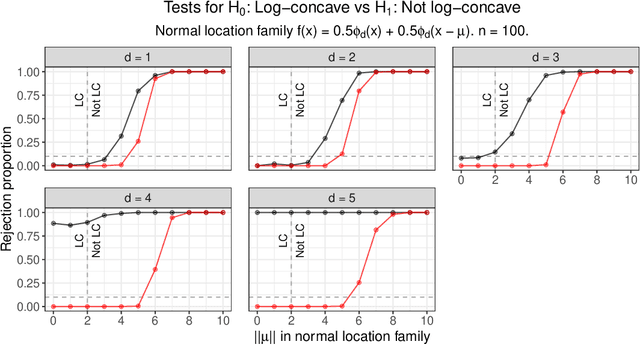
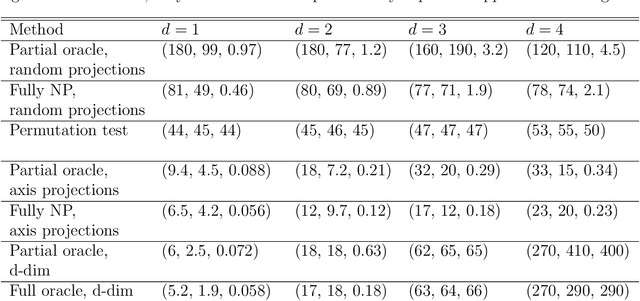
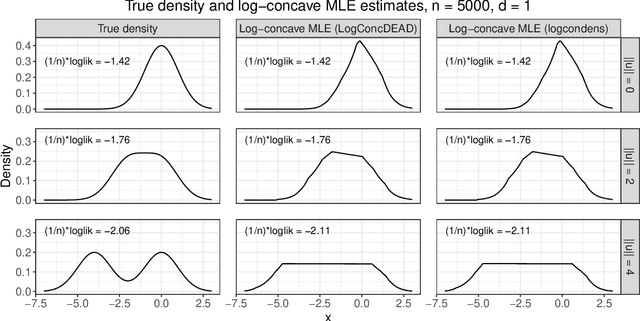
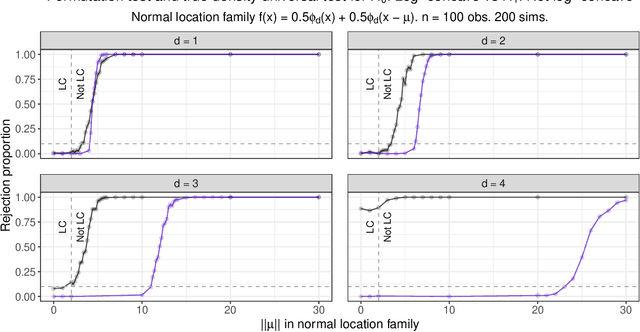
Shape constraints yield flexible middle grounds between fully nonparametric and fully parametric approaches to modeling distributions of data. The specific assumption of log-concavity is motivated by applications across economics, survival modeling, and reliability theory. However, there do not currently exist valid tests for whether the underlying density of given data is log-concave. The recent universal likelihood ratio test provides a valid test. The universal test relies on maximum likelihood estimation (MLE), and efficient methods already exist for finding the log-concave MLE. This yields the first test of log-concavity that is provably valid in finite samples in any dimension, for which we also establish asymptotic consistency results. Empirically, we find that the highest power is obtained by using random projections to convert the d-dimensional testing problem into many one-dimensional problems, leading to a simple procedure that is statistically and computationally efficient.