Counterfactual Fairness

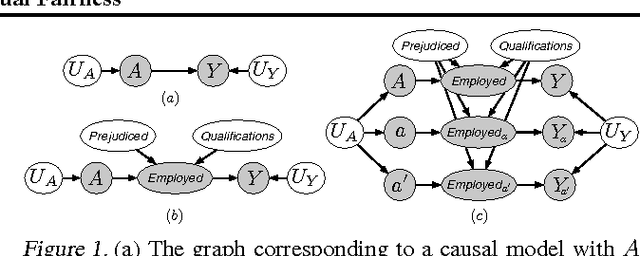
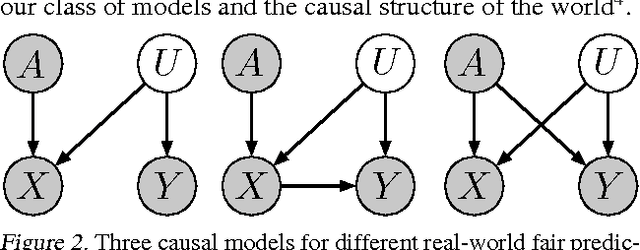
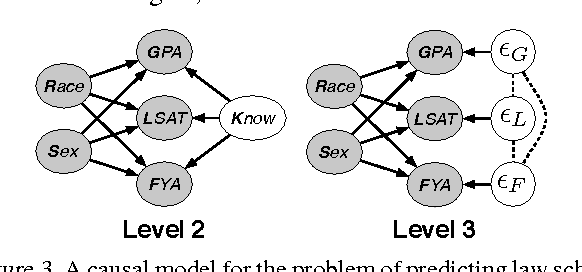
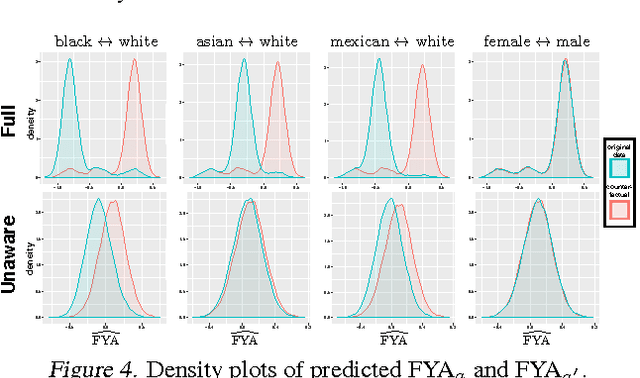
Machine learning can impact people with legal or ethical consequences when it is used to automate decisions in areas such as insurance, lending, hiring, and predictive policing. In many of these scenarios, previous decisions have been made that are unfairly biased against certain subpopulations, for example those of a particular race, gender, or sexual orientation. Since this past data may be biased, machine learning predictors must account for this to avoid perpetuating or creating discriminatory practices. In this paper, we develop a framework for modeling fairness using tools from causal inference. Our definition of counterfactual fairness captures the intuition that a decision is fair towards an individual if it is the same in (a) the actual world and (b) a counterfactual world where the individual belonged to a different demographic group. We demonstrate our framework on a real-world problem of fair prediction of success in law school.

A Dynamic Edge Exchangeable Model for Sparse Temporal Networks

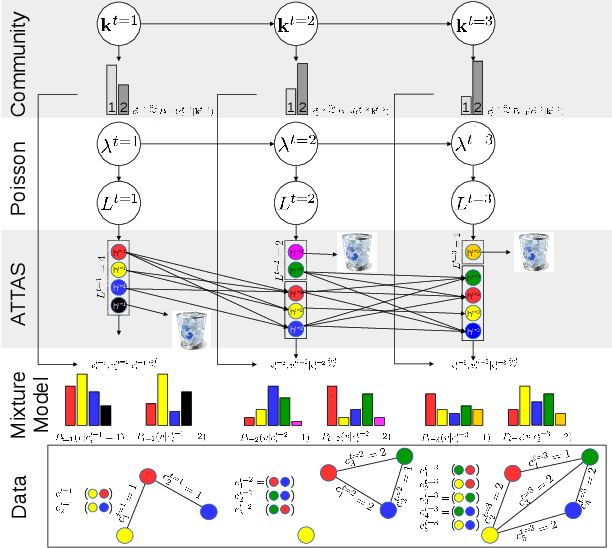
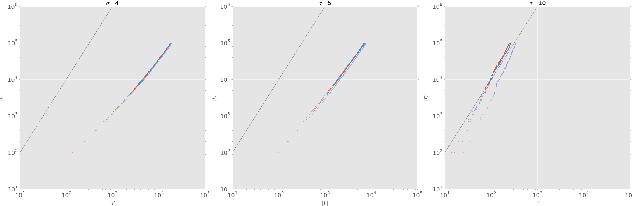
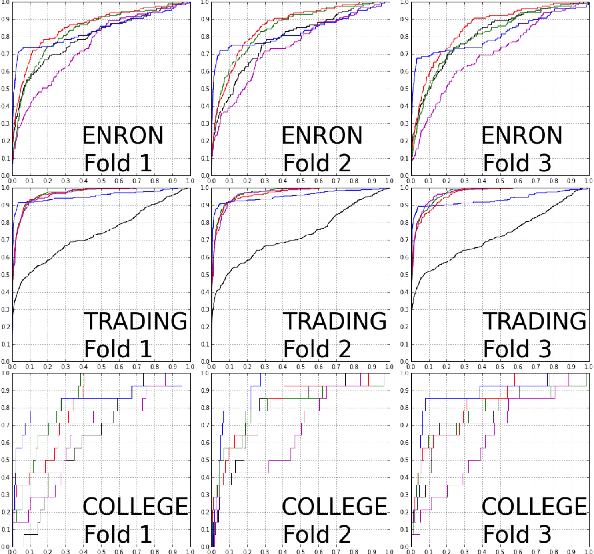
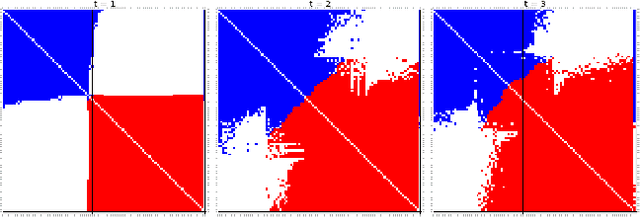
We propose a dynamic edge exchangeable network model that can capture sparse connections observed in real temporal networks, in contrast to existing models which are dense. The model achieved superior link prediction accuracy on multiple data sets when compared to a dynamic variant of the blockmodel, and is able to extract interpretable time-varying community structures from the data. In addition to sparsity, the model accounts for the effect of social influence on vertices' future behaviours. Compared to the dynamic blockmodels, our model has a smaller latent space. The compact latent space requires a smaller number of parameters to be estimated in variational inference and results in a computationally friendly inference algorithm.

Scaling Factorial Hidden Markov Models: Stochastic Variational Inference without Messages

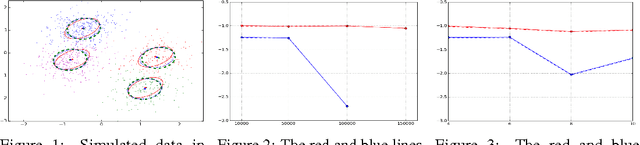
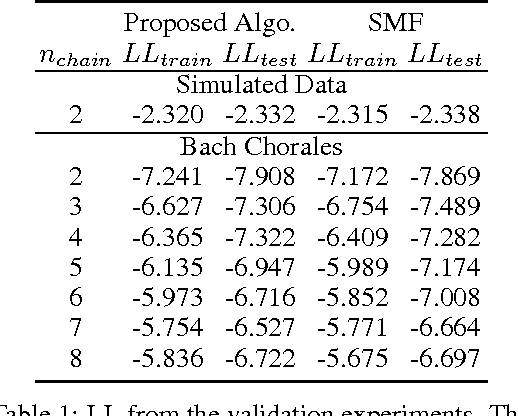
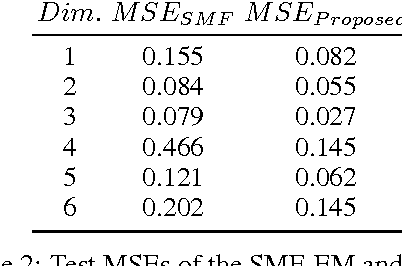
Factorial Hidden Markov Models (FHMMs) are powerful models for sequential data but they do not scale well with long sequences. We propose a scalable inference and learning algorithm for FHMMs that draws on ideas from the stochastic variational inference, neural network and copula literatures. Unlike existing approaches, the proposed algorithm requires no message passing procedure among latent variables and can be distributed to a network of computers to speed up learning. Our experiments corroborate that the proposed algorithm does not introduce further approximation bias compared to the proven structured mean-field algorithm, and achieves better performance with long sequences and large FHMMs.

Observational-Interventional Priors for Dose-Response Learning

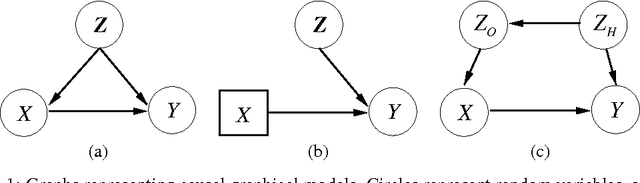
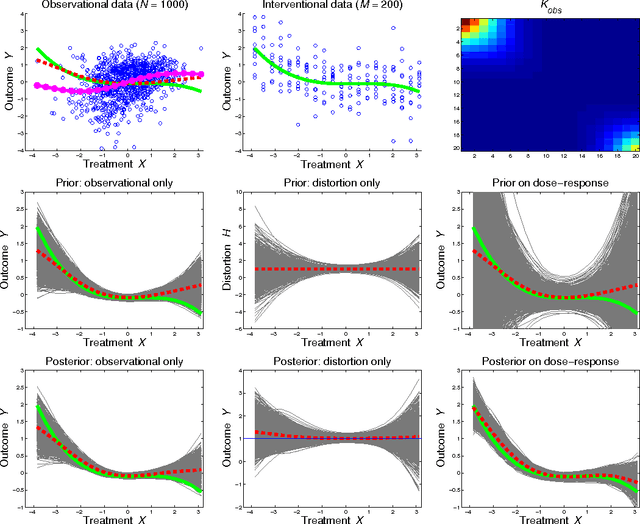
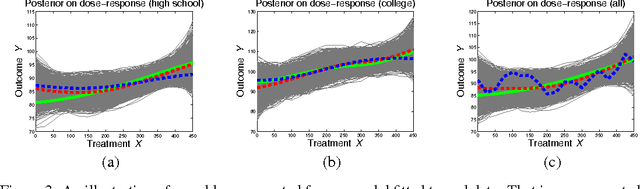
Controlled interventions provide the most direct source of information for learning causal effects. In particular, a dose-response curve can be learned by varying the treatment level and observing the corresponding outcomes. However, interventions can be expensive and time-consuming. Observational data, where the treatment is not controlled by a known mechanism, is sometimes available. Under some strong assumptions, observational data allows for the estimation of dose-response curves. Estimating such curves nonparametrically is hard: sample sizes for controlled interventions may be small, while in the observational case a large number of measured confounders may need to be marginalized. In this paper, we introduce a hierarchical Gaussian process prior that constructs a distribution over the dose-response curve by learning from observational data, and reshapes the distribution with a nonparametric affine transform learned from controlled interventions. This function composition from different sources is shown to speed-up learning, which we demonstrate with a thorough sensitivity analysis and an application to modeling the effect of therapy on cognitive skills of premature infants.

Bayesian Inference in Cumulative Distribution Fields

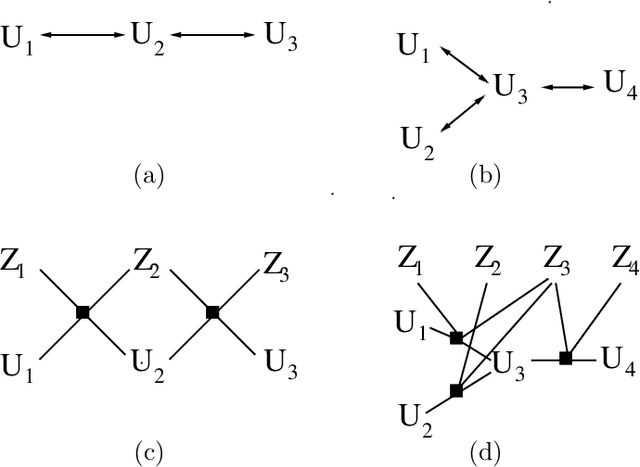
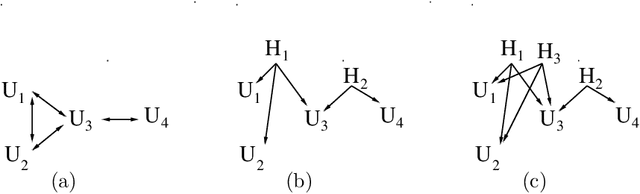
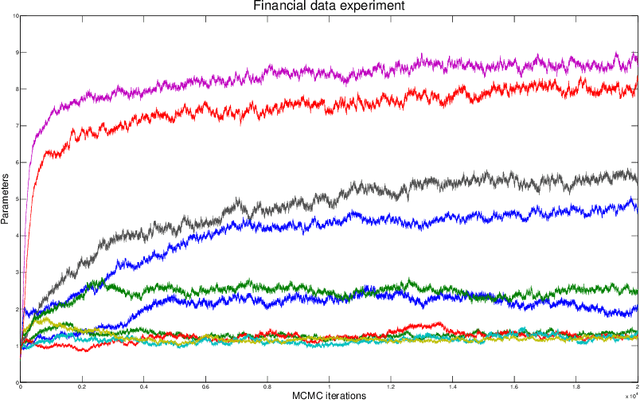
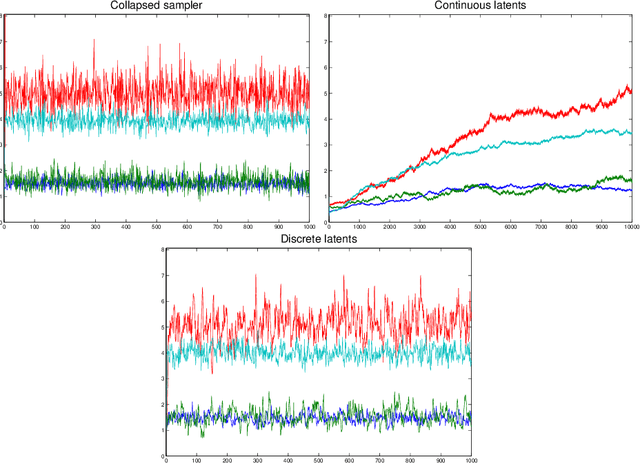
One approach for constructing copula functions is by multiplication. Given that products of cumulative distribution functions (CDFs) are also CDFs, an adjustment to this multiplication will result in a copula model, as discussed by Liebscher (J Mult Analysis, 2008). Parameterizing models via products of CDFs has some advantages, both from the copula perspective (e.g., it is well-defined for any dimensionality) and from general multivariate analysis (e.g., it provides models where small dimensional marginal distributions can be easily read-off from the parameters). Independently, Huang and Frey (J Mach Learn Res, 2011) showed the connection between certain sparse graphical models and products of CDFs, as well as message-passing (dynamic programming) schemes for computing the likelihood function of such models. Such schemes allows models to be estimated with likelihood-based methods. We discuss and demonstrate MCMC approaches for estimating such models in a Bayesian context, their application in copula modeling, and how message-passing can be strongly simplified. Importantly, our view of message-passing opens up possibilities to scaling up such methods, given that even dynamic programming is not a scalable solution for calculating likelihood functions in many models.

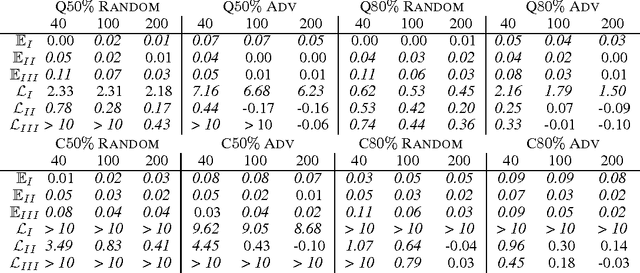
Learning Instrumental Variables with Non-Gaussianity Assumptions: Theoretical Limitations and Practical Algorithms

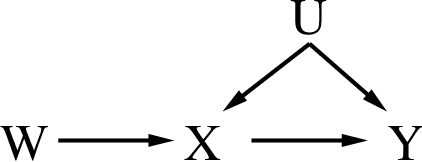
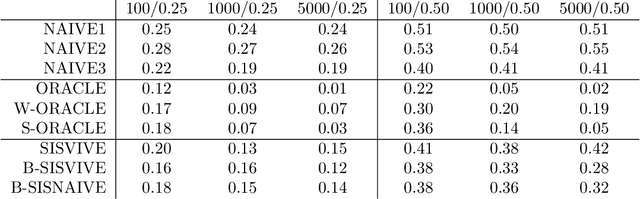
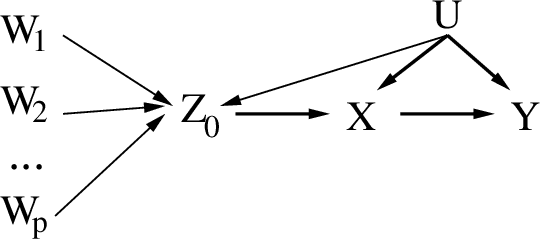
Learning a causal effect from observational data is not straightforward, as this is not possible without further assumptions. If hidden common causes between treatment $X$ and outcome $Y$ cannot be blocked by other measurements, one possibility is to use an instrumental variable. In principle, it is possible under some assumptions to discover whether a variable is structurally instrumental to a target causal effect $X \rightarrow Y$, but current frameworks are somewhat lacking on how general these assumptions can be. A instrumental variable discovery problem is challenging, as no variable can be tested as an instrument in isolation but only in groups, but different variables might require different conditions to be considered an instrument. Moreover, identification constraints might be hard to detect statistically. In this paper, we give a theoretical characterization of instrumental variable discovery, highlighting identifiability problems and solutions, the need for non-Gaussianity assumptions, and how they fit within existing methods.

Causal Inference through a Witness Protection Program

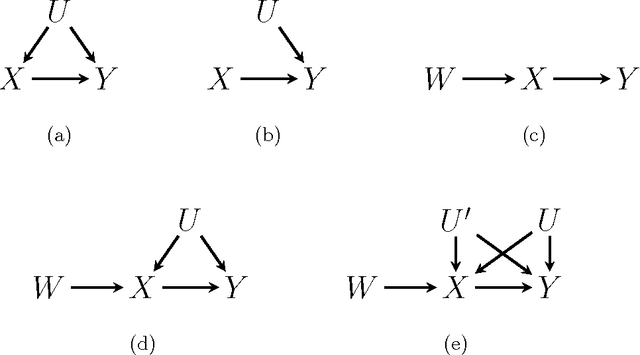
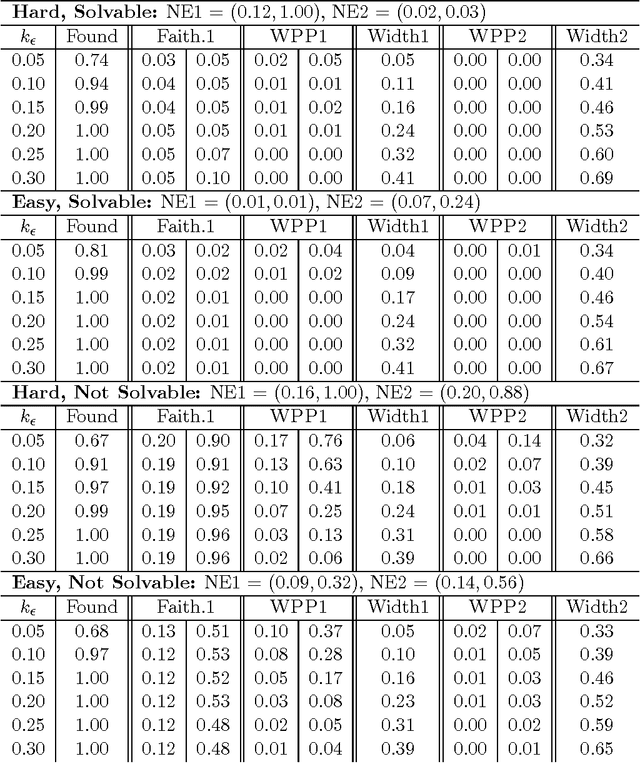
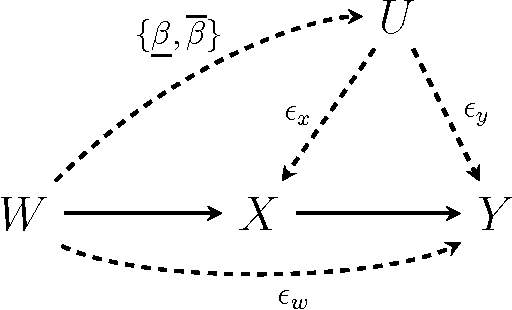
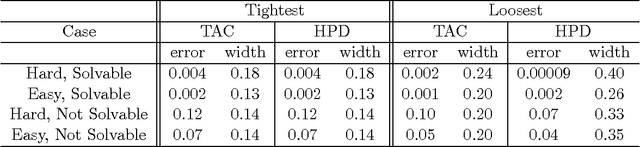
One of the most fundamental problems in causal inference is the estimation of a causal effect when variables are confounded. This is difficult in an observational study, because one has no direct evidence that all confounders have been adjusted for. We introduce a novel approach for estimating causal effects that exploits observational conditional independencies to suggest "weak" paths in a unknown causal graph. The widely used faithfulness condition of Spirtes et al. is relaxed to allow for varying degrees of "path cancellations" that imply conditional independencies but do not rule out the existence of confounding causal paths. The outcome is a posterior distribution over bounds on the average causal effect via a linear programming approach and Bayesian inference. We claim this approach should be used in regular practice along with other default tools in observational studies.

Gaussian Process Structural Equation Models with Latent Variables

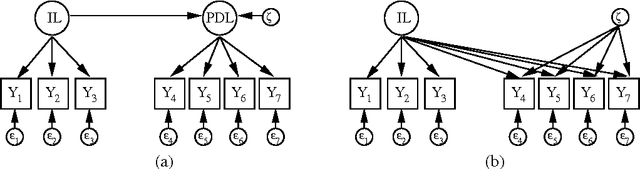
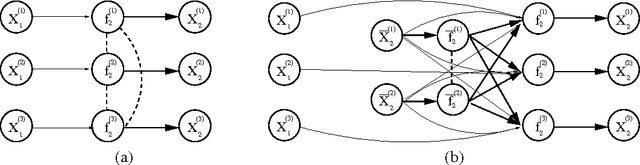
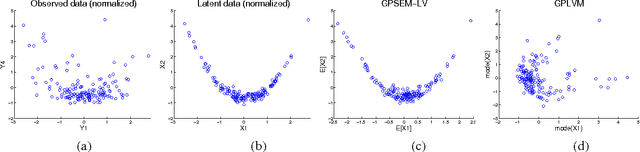
In a variety of disciplines such as social sciences, psychology, medicine and economics, the recorded data are considered to be noisy measurements of latent variables connected by some causal structure. This corresponds to a family of graphical models known as the structural equation model with latent variables. While linear non-Gaussian variants have been well-studied, inference in nonparametric structural equation models is still underdeveloped. We introduce a sparse Gaussian process parameterization that defines a non-linear structure connecting latent variables, unlike common formulations of Gaussian process latent variable models. The sparse parameterization is given a full Bayesian treatment without compromising Markov chain Monte Carlo efficiency. We compare the stability of the sampling procedure and the predictive ability of the model against the current practice.

Flexible sampling of discrete data correlations without the marginal distributions

Learning the joint dependence of discrete variables is a fundamental problem in machine learning, with many applications including prediction, clustering and dimensionality reduction. More recently, the framework of copula modeling has gained popularity due to its modular parametrization of joint distributions. Among other properties, copulas provide a recipe for combining flexible models for univariate marginal distributions with parametric families suitable for potentially high dimensional dependence structures. More radically, the extended rank likelihood approach of Hoff (2007) bypasses learning marginal models completely when such information is ancillary to the learning task at hand as in, e.g., standard dimensionality reduction problems or copula parameter estimation. The main idea is to represent data by their observable rank statistics, ignoring any other information from the marginals. Inference is typically done in a Bayesian framework with Gaussian copulas, and it is complicated by the fact this implies sampling within a space where the number of constraints increases quadratically with the number of data points. The result is slow mixing when using off-the-shelf Gibbs sampling. We present an efficient algorithm based on recent advances on constrained Hamiltonian Markov chain Monte Carlo that is simple to implement and does not require paying for a quadratic cost in sample size.

Ranking relations using analogies in biological and information networks

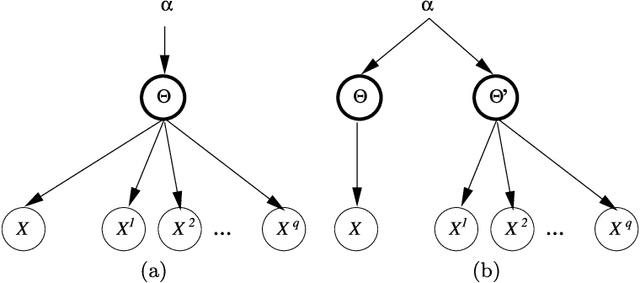
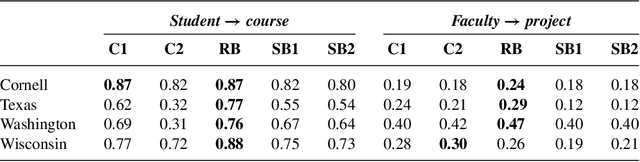
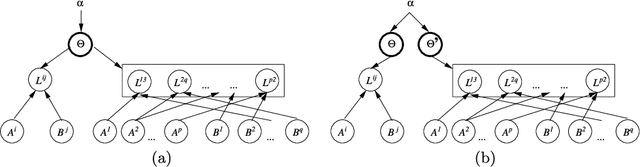
Analogical reasoning depends fundamentally on the ability to learn and generalize about relations between objects. We develop an approach to relational learning which, given a set of pairs of objects $\mathbf{S}=\{A^{(1)}:B^{(1)},A^{(2)}:B^{(2)},\ldots,A^{(N)}:B ^{(N)}\}$, measures how well other pairs A:B fit in with the set $\mathbf{S}$. Our work addresses the following question: is the relation between objects A and B analogous to those relations found in $\mathbf{S}$? Such questions are particularly relevant in information retrieval, where an investigator might want to search for analogous pairs of objects that match the query set of interest. There are many ways in which objects can be related, making the task of measuring analogies very challenging. Our approach combines a similarity measure on function spaces with Bayesian analysis to produce a ranking. It requires data containing features of the objects of interest and a link matrix specifying which relationships exist; no further attributes of such relationships are necessary. We illustrate the potential of our method on text analysis and information networks. An application on discovering functional interactions between pairs of proteins is discussed in detail, where we show that our approach can work in practice even if a small set of protein pairs is provided.