Private Algorithms for Stochastic Saddle Points and Variational Inequalities: Beyond Euclidean Geometry

In this work, we conduct a systematic study of stochastic saddle point problems (SSP) and stochastic variational inequalities (SVI) under the constraint of $(\epsilon,\delta)$-differential privacy (DP) in both Euclidean and non-Euclidean setups. We first consider Lipschitz convex-concave SSPs in the $\ell_p/\ell_q$ setup, $p,q\in[1,2]$. Here, we obtain a bound of $\tilde{O}\big(\frac{1}{\sqrt{n}} + \frac{\sqrt{d}}{n\epsilon}\big)$ on the strong SP-gap, where $n$ is the number of samples and $d$ is the dimension. This rate is nearly optimal for any $p,q\in[1,2]$. Without additional assumptions, such as smoothness or linearity requirements, prior work under DP has only obtained this rate when $p=q=2$ (i.e., only in the Euclidean setup). Further, existing algorithms have each only been shown to work for specific settings of $p$ and $q$ and under certain assumptions on the loss and the feasible set, whereas we provide a general algorithm for DP SSPs whenever $p,q\in[1,2]$. Our result is obtained via a novel analysis of the recursive regularization algorithm. In particular, we develop new tools for analyzing generalization, which may be of independent interest. Next, we turn our attention towards SVIs with a monotone, bounded and Lipschitz operator and consider $\ell_p$-setups, $p\in[1,2]$. Here, we provide the first analysis which obtains a bound on the strong VI-gap of $\tilde{O}\big(\frac{1}{\sqrt{n}} + \frac{\sqrt{d}}{n\epsilon}\big)$. For $p-1=\Omega(1)$, this rate is near optimal due to existing lower bounds. To obtain this result, we develop a modified version of recursive regularization. Our analysis builds on the techniques we develop for SSPs as well as employing additional novel components which handle difficulties arising from adapting the recursive regularization framework to SVIs.

Public-data Assisted Private Stochastic Optimization: Power and Limitations

We study the limits and capability of public-data assisted differentially private (PA-DP) algorithms. Specifically, we focus on the problem of stochastic convex optimization (SCO) with either labeled or unlabeled public data. For complete/labeled public data, we show that any $(\epsilon,\delta)$-PA-DP has excess risk $\tilde{\Omega}\big(\min\big\{\frac{1}{\sqrt{n_{\text{pub}}}},\frac{1}{\sqrt{n}}+\frac{\sqrt{d}}{n\epsilon} \big\} \big)$, where $d$ is the dimension, ${n_{\text{pub}}}$ is the number of public samples, ${n_{\text{priv}}}$ is the number of private samples, and $n={n_{\text{pub}}}+{n_{\text{priv}}}$. These lower bounds are established via our new lower bounds for PA-DP mean estimation, which are of a similar form. Up to constant factors, these lower bounds show that the simple strategy of either treating all data as private or discarding the private data, is optimal. We also study PA-DP supervised learning with \textit{unlabeled} public samples. In contrast to our previous result, we here show novel methods for leveraging public data in private supervised learning. For generalized linear models (GLM) with unlabeled public data, we show an efficient algorithm which, given $\tilde{O}({n_{\text{priv}}}\epsilon)$ unlabeled public samples, achieves the dimension independent rate $\tilde{O}\big(\frac{1}{\sqrt{{n_{\text{priv}}}}} + \frac{1}{\sqrt{{n_{\text{priv}}}\epsilon}}\big)$. We develop new lower bounds for this setting which shows that this rate cannot be improved with more public samples, and any fewer public samples leads to a worse rate. Finally, we provide extensions of this result to general hypothesis classes with finite fat-shattering dimension with applications to neural networks and non-Euclidean geometries.

Differentially Private Worst-group Risk Minimization

We initiate a systematic study of worst-group risk minimization under $(\epsilon, \delta)$-differential privacy (DP). The goal is to privately find a model that approximately minimizes the maximal risk across $p$ sub-populations (groups) with different distributions, where each group distribution is accessed via a sample oracle. We first present a new algorithm that achieves excess worst-group population risk of $\tilde{O}(\frac{p\sqrt{d}}{K\epsilon} + \sqrt{\frac{p}{K}})$, where $K$ is the total number of samples drawn from all groups and $d$ is the problem dimension. Our rate is nearly optimal when each distribution is observed via a fixed-size dataset of size $K/p$. Our result is based on a new stability-based analysis for the generalization error. In particular, we show that $\Delta$-uniform argument stability implies $\tilde{O}(\Delta + \frac{1}{\sqrt{n}})$ generalization error w.r.t. the worst-group risk, where $n$ is the number of samples drawn from each sample oracle. Next, we propose an algorithmic framework for worst-group population risk minimization using any DP online convex optimization algorithm as a subroutine. Hence, we give another excess risk bound of $\tilde{O}\left( \sqrt{\frac{d^{1/2}}{\epsilon K}} +\sqrt{\frac{p}{K\epsilon^2}} \right)$. Assuming the typical setting of $\epsilon=\Theta(1)$, this bound is more favorable than our first bound in a certain range of $p$ as a function of $K$ and $d$. Finally, we study differentially private worst-group empirical risk minimization in the offline setting, where each group distribution is observed by a fixed-size dataset. We present a new algorithm with nearly optimal excess risk of $\tilde{O}(\frac{p\sqrt{d}}{K\epsilon})$.

Differentially Private Non-Convex Optimization under the KL Condition with Optimal Rates

We study private empirical risk minimization (ERM) problem for losses satisfying the $(\gamma,\kappa)$-Kurdyka-{\L}ojasiewicz (KL) condition. The Polyak-{\L}ojasiewicz (PL) condition is a special case of this condition when $\kappa=2$. Specifically, we study this problem under the constraint of $\rho$ zero-concentrated differential privacy (zCDP). When $\kappa\in[1,2]$ and the loss function is Lipschitz and smooth over a sufficiently large region, we provide a new algorithm based on variance reduced gradient descent that achieves the rate $\tilde{O}\big(\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)^\kappa\big)$ on the excess empirical risk, where $n$ is the dataset size and $d$ is the dimension. We further show that this rate is nearly optimal. When $\kappa \geq 2$ and the loss is instead Lipschitz and weakly convex, we show it is possible to achieve the rate $\tilde{O}\big(\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)^\kappa\big)$ with a private implementation of the proximal point method. When the KL parameters are unknown, we provide a novel modification and analysis of the noisy gradient descent algorithm and show that this algorithm achieves a rate of $\tilde{O}\big(\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)^{\frac{2\kappa}{4-\kappa}}\big)$ adaptively, which is nearly optimal when $\kappa = 2$. We further show that, without assuming the KL condition, the same gradient descent algorithm can achieve fast convergence to a stationary point when the gradient stays sufficiently large during the run of the algorithm. Specifically, we show that this algorithm can approximate stationary points of Lipschitz, smooth (and possibly nonconvex) objectives with rate as fast as $\tilde{O}\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)$ and never worse than $\tilde{O}\big(\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)^{1/2}\big)$. The latter rate matches the best known rate for methods that do not rely on variance reduction.

Differentially Private Domain Adaptation with Theoretical Guarantees

In many applications, the labeled data at the learner's disposal is subject to privacy constraints and is relatively limited. To derive a more accurate predictor for the target domain, it is often beneficial to leverage publicly available labeled data from an alternative domain, somewhat close to the target domain. This is the modern problem of supervised domain adaptation from a public source to a private target domain. We present two $(\epsilon, \delta)$-differentially private adaptation algorithms for supervised adaptation, for which we make use of a general optimization problem, recently shown to benefit from favorable theoretical learning guarantees. Our first algorithm is designed for regression with linear predictors and shown to solve a convex optimization problem. Our second algorithm is a more general solution for loss functions that may be non-convex but Lipschitz and smooth. While our main objective is a theoretical analysis, we also report the results of several experiments first demonstrating that the non-private versions of our algorithms outperform adaptation baselines and next showing that, for larger values of the target sample size or $\epsilon$, the performance of our private algorithms remains close to that of the non-private formulation.

Differentially Private Algorithms for the Stochastic Saddle Point Problem with Optimal Rates for the Strong Gap

We show that convex-concave Lipschitz stochastic saddle point problems (also known as stochastic minimax optimization) can be solved under the constraint of $(\epsilon,\delta)$-differential privacy with \emph{strong (primal-dual) gap} rate of $\tilde O\big(\frac{1}{\sqrt{n}} + \frac{\sqrt{d}}{n\epsilon}\big)$, where $n$ is the dataset size and $d$ is the dimension of the problem. This rate is nearly optimal, based on existing lower bounds in differentially private stochastic optimization. Specifically, we prove a tight upper bound on the strong gap via novel implementation and analysis of the recursive regularization technique repurposed for saddle point problems. We show that this rate can be attained with $O\big(\min\big\{\frac{n^2\epsilon^{1.5}}{\sqrt{d}}, n^{3/2}\big\}\big)$ gradient complexity, and $O(n)$ gradient complexity if the loss function is smooth. As a byproduct of our method, we develop a general algorithm that, given a black-box access to a subroutine satisfying a certain $\alpha$ primal-dual accuracy guarantee with respect to the empirical objective, gives a solution to the stochastic saddle point problem with a strong gap of $\tilde{O}(\alpha+\frac{1}{\sqrt{n}})$. We show that this $\alpha$-accuracy condition is satisfied by standard algorithms for the empirical saddle point problem such as the proximal point method and the stochastic gradient descent ascent algorithm. Further, we show that even for simple problems it is possible for an algorithm to have zero weak gap and suffer from $\Omega(1)$ strong gap. We also show that there exists a fundamental tradeoff between stability and accuracy. Specifically, we show that any $\Delta$-stable algorithm has empirical gap $\Omega\big(\frac{1}{\Delta n}\big)$, and that this bound is tight. This result also holds also more specifically for empirical risk minimization problems and may be of independent interest.

Private Domain Adaptation from a Public Source

A key problem in a variety of applications is that of domain adaptation from a public source domain, for which a relatively large amount of labeled data with no privacy constraints is at one's disposal, to a private target domain, for which a private sample is available with very few or no labeled data. In regression problems with no privacy constraints on the source or target data, a discrepancy minimization algorithm based on several theoretical guarantees was shown to outperform a number of other adaptation algorithm baselines. Building on that approach, we design differentially private discrepancy-based algorithms for adaptation from a source domain with public labeled data to a target domain with unlabeled private data. The design and analysis of our private algorithms critically hinge upon several key properties we prove for a smooth approximation of the weighted discrepancy, such as its smoothness with respect to the $\ell_1$-norm and the sensitivity of its gradient. Our solutions are based on private variants of Frank-Wolfe and Mirror-Descent algorithms. We show that our adaptation algorithms benefit from strong generalization and privacy guarantees and report the results of experiments demonstrating their effectiveness.

Faster Rates of Convergence to Stationary Points in Differentially Private Optimization

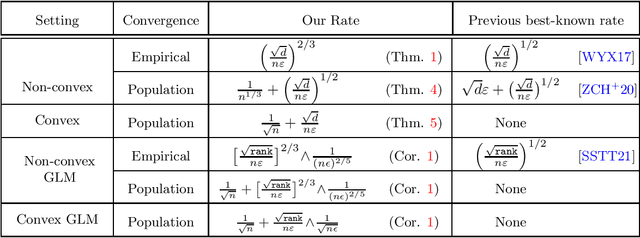
We study the problem of approximating stationary points of Lipschitz and smooth functions under $(\varepsilon,\delta)$-differential privacy (DP) in both the finite-sum and stochastic settings. A point $\widehat{w}$ is called an $\alpha$-stationary point of a function $F:\mathbb{R}^d\rightarrow\mathbb{R}$ if $\|\nabla F(\widehat{w})\|\leq \alpha$. We provide a new efficient algorithm that finds an $\tilde{O}\big(\big[\frac{\sqrt{d}}{n\varepsilon}\big]^{2/3}\big)$-stationary point in the finite-sum setting, where $n$ is the number of samples. This improves on the previous best rate of $\tilde{O}\big(\big[\frac{\sqrt{d}}{n\varepsilon}\big]^{1/2}\big)$. We also give a new construction that improves over the existing rates in the stochastic optimization setting, where the goal is to find approximate stationary points of the population risk. Our construction finds a $\tilde{O}\big(\frac{1}{n^{1/3}} + \big[\frac{\sqrt{d}}{n\varepsilon}\big]^{1/2}\big)$-stationary point of the population risk in time linear in $n$. Furthermore, under the additional assumption of convexity, we completely characterize the sample complexity of finding stationary points of the population risk (up to polylog factors) and show that the optimal rate on population stationarity is $\tilde \Theta\big(\frac{1}{\sqrt{n}}+\frac{\sqrt{d}}{n\varepsilon}\big)$. Finally, we show that our methods can be used to provide dimension-independent rates of $O\big(\frac{1}{\sqrt{n}}+\min\big(\big[\frac{\sqrt{rank}}{n\varepsilon}\big]^{2/3},\frac{1}{(n\varepsilon)^{2/5}}\big)\big)$ on population stationarity for Generalized Linear Models (GLM), where $rank$ is the rank of the design matrix, which improves upon the previous best known rate.

Differentially Private Generalized Linear Models Revisited

We study the problem of $(\epsilon,\delta)$-differentially private learning of linear predictors with convex losses. We provide results for two subclasses of loss functions. The first case is when the loss is smooth and non-negative but not necessarily Lipschitz (such as the squared loss). For this case, we establish an upper bound on the excess population risk of $\tilde{O}\left(\frac{\Vert w^*\Vert}{\sqrt{n}} + \min\left\{\frac{\Vert w^* \Vert^2}{(n\epsilon)^{2/3}},\frac{\sqrt{d}\Vert w^*\Vert^2}{n\epsilon}\right\}\right)$, where $n$ is the number of samples, $d$ is the dimension of the problem, and $w^*$ is the minimizer of the population risk. Apart from the dependence on $\Vert w^\ast\Vert$, our bound is essentially tight in all parameters. In particular, we show a lower bound of $\tilde{\Omega}\left(\frac{1}{\sqrt{n}} + {\min\left\{\frac{\Vert w^*\Vert^{4/3}}{(n\epsilon)^{2/3}}, \frac{\sqrt{d}\Vert w^*\Vert}{n\epsilon}\right\}}\right)$. We also revisit the previously studied case of Lipschitz losses [SSTT20]. For this case, we close the gap in the existing work and show that the optimal rate is (up to log factors) $\Theta\left(\frac{\Vert w^*\Vert}{\sqrt{n}} + \min\left\{\frac{\Vert w^*\Vert}{\sqrt{n\epsilon}},\frac{\sqrt{\text{rank}}\Vert w^*\Vert}{n\epsilon}\right\}\right)$, where $\text{rank}$ is the rank of the design matrix. This improves over existing work in the high privacy regime. Finally, our algorithms involve a private model selection approach that we develop to enable attaining the stated rates without a-priori knowledge of $\Vert w^*\Vert$.

Differentially Private Learning with Margin Guarantees

We present a series of new differentially private (DP) algorithms with dimension-independent margin guarantees. For the family of linear hypotheses, we give a pure DP learning algorithm that benefits from relative deviation margin guarantees, as well as an efficient DP learning algorithm with margin guarantees. We also present a new efficient DP learning algorithm with margin guarantees for kernel-based hypotheses with shift-invariant kernels, such as Gaussian kernels, and point out how our results can be extended to other kernels using oblivious sketching techniques. We further give a pure DP learning algorithm for a family of feed-forward neural networks for which we prove margin guarantees that are independent of the input dimension. Additionally, we describe a general label DP learning algorithm, which benefits from relative deviation margin bounds and is applicable to a broad family of hypothesis sets, including that of neural networks. Finally, we show how our DP learning algorithms can be augmented in a general way to include model selection, to select the best confidence margin parameter.