Stable Weight Updating: A Key to Reliable PDE Solutions Using Deep Learning

Background: Deep learning techniques, particularly neural networks, have revolutionized computational physics, offering powerful tools for solving complex partial differential equations (PDEs). However, ensuring stability and efficiency remains a challenge, especially in scenarios involving nonlinear and time-dependent equations. Methodology: This paper introduces novel residual-based architectures, namely the Simple Highway Network and the Squared Residual Network, designed to enhance stability and accuracy in physics-informed neural networks (PINNs). These architectures augment traditional neural networks by incorporating residual connections, which facilitate smoother weight updates and improve backpropagation efficiency. Results: Through extensive numerical experiments across various examples including linear and nonlinear, time-dependent and independent PDEs we demonstrate the efficacy of the proposed architectures. The Squared Residual Network, in particular, exhibits robust performance, achieving enhanced stability and accuracy compared to conventional neural networks. These findings underscore the potential of residual-based architectures in advancing deep learning for PDEs and computational physics applications.

Computing Topology Preservation of RBF Transformations for Landmark-Based Image Registration

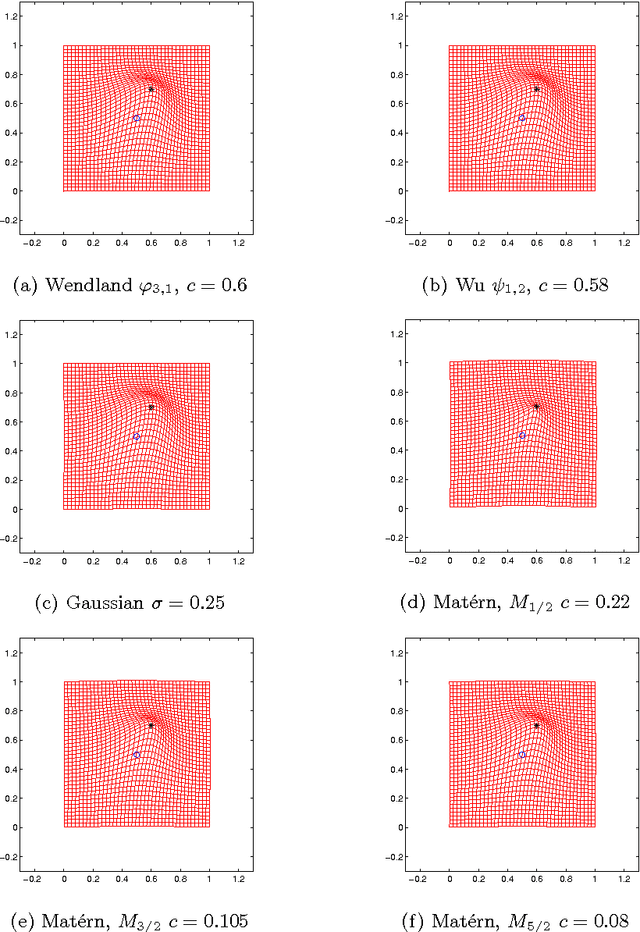
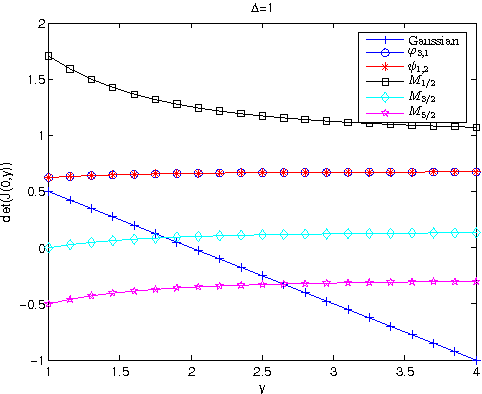
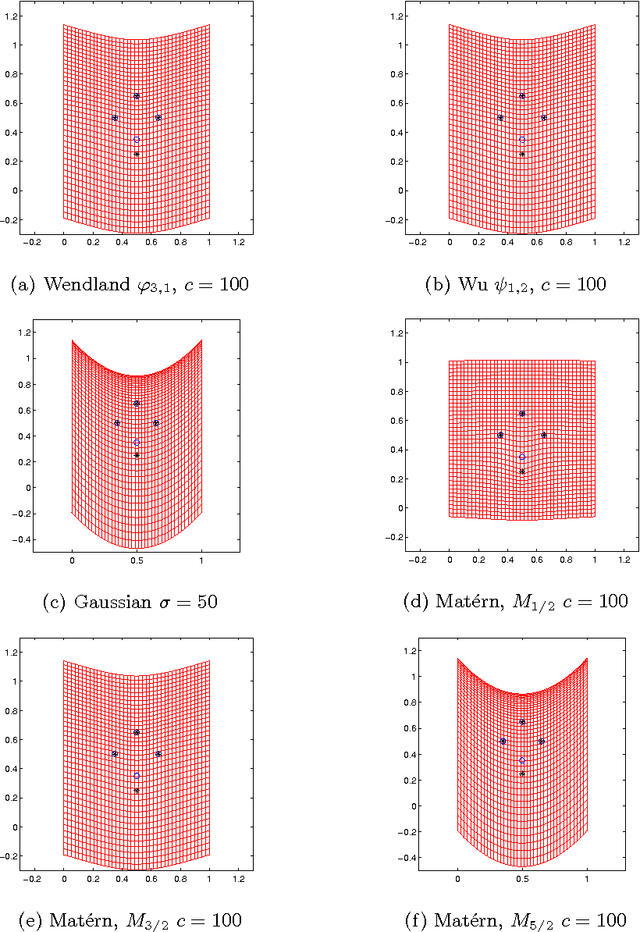
In image registration, a proper transformation should be topology preserving. Especially for landmark-based image registration, if the displacement of one landmark is larger enough than those of neighbourhood landmarks, topology violation will be occurred. This paper aim to analyse the topology preservation of some Radial Basis Functions (RBFs) which are used to model deformations in image registration. Mat\'{e}rn functions are quite common in the statistic literature (see, e.g. \cite{Matern86,Stein99}). In this paper, we use them to solve the landmark-based image registration problem. We present the topology preservation properties of RBFs in one landmark and four landmarks model respectively. Numerical results of three kinds of Mat\'{e}rn transformations are compared with results of Gaussian, Wendland's, and Wu's functions.