Smooth Alternating Direction Methods for Nonsmooth Constrained Convex Optimization

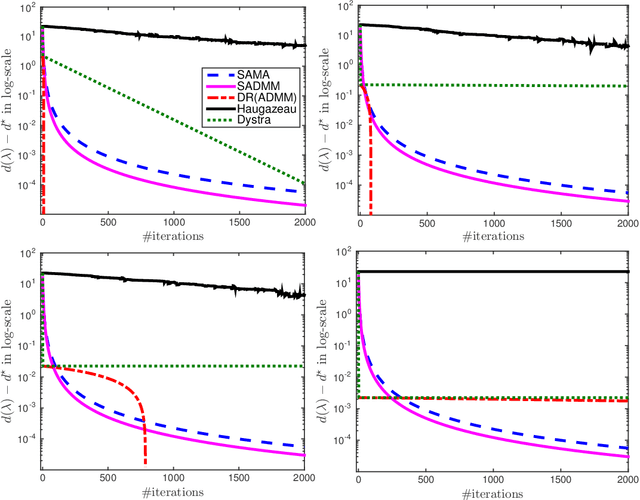
We propose two new alternating direction methods to solve "fully" nonsmooth constrained convex problems. Our algorithms have the best known worst-case iteration-complexity guarantee under mild assumptions for both the objective residual and feasibility gap. Through theoretical analysis, we show how to update all the algorithmic parameters automatically with clear impact on the convergence performance. We also provide a representative numerical example showing the advantages of our methods over the classical alternating direction methods using a well-known feasibility problem.

Smooth Primal-Dual Coordinate Descent Algorithms for Nonsmooth Convex Optimization

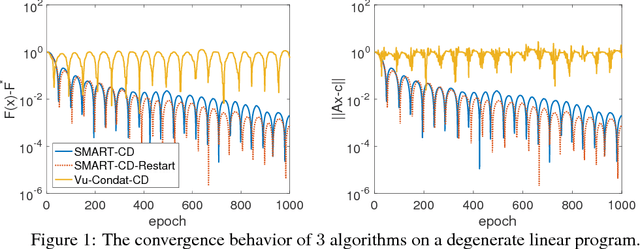
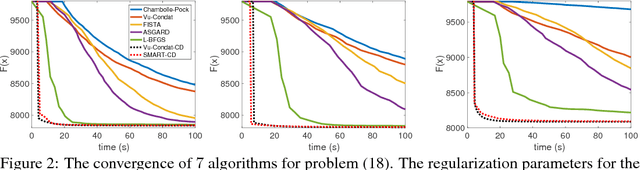
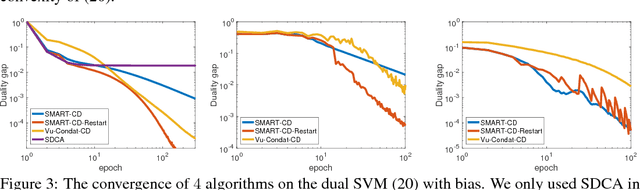
We propose a new randomized coordinate descent method for a convex optimization template with broad applications. Our analysis relies on a novel combination of four ideas applied to the primal-dual gap function: smoothing, acceleration, homotopy, and coordinate descent with non-uniform sampling. As a result, our method features the first convergence rate guarantees among the coordinate descent methods, that are the best-known under a variety of common structure assumptions on the template. We provide numerical evidence to support the theoretical results with a comparison to state-of-the-art algorithms.

A single-phase, proximal path-following framework

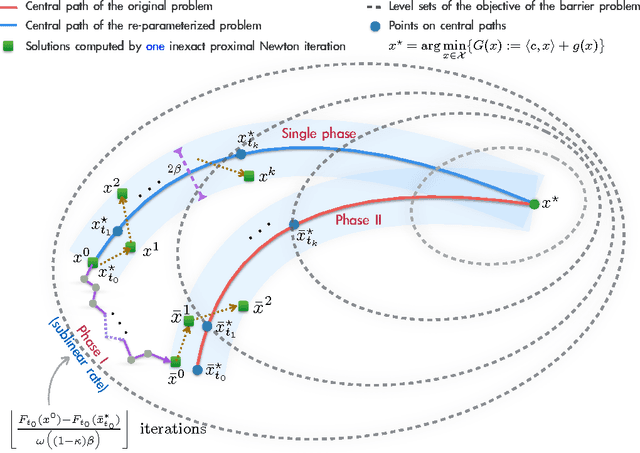
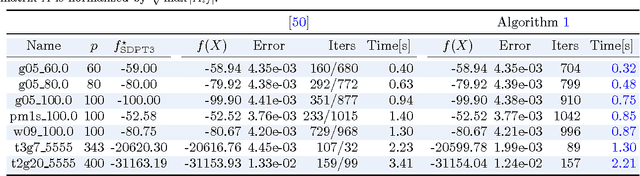
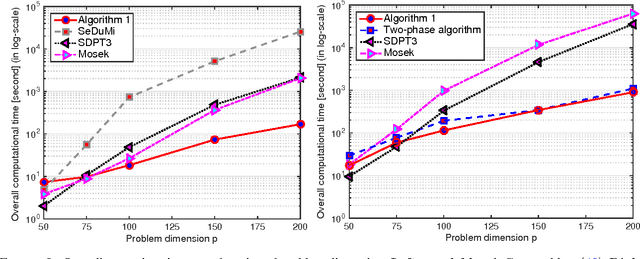
We propose a new proximal, path-following framework for a class of constrained convex problems. We consider settings where the nonlinear---and possibly non-smooth---objective part is endowed with a proximity operator, and the constraint set is equipped with a self-concordant barrier. Our approach relies on the following two main ideas. First, we re-parameterize the optimality condition as an auxiliary problem, such that a good initial point is available; by doing so, a family of alternative paths towards the optimum is generated. Second, we combine the proximal operator with path-following ideas to design a single-phase, proximal, path-following algorithm. Our method has several advantages. First, it allows handling non-smooth objectives via proximal operators; this avoids lifting the problem dimension in order to accommodate non-smooth components in optimization. Second, it consists of only a \emph{single phase}: While the overall convergence rate of classical path-following schemes for self-concordant objectives does not suffer from the initialization phase, proximal path-following schemes undergo slow convergence, in order to obtain a good starting point \cite{TranDinh2013e}. In this work, we show how to overcome this limitation in the proximal setting and prove that our scheme has the same $\mathcal{O}(\sqrt{\nu}\log(1/\varepsilon))$ worst-case iteration-complexity with standard approaches \cite{Nesterov2004,Nesterov1994} without requiring an initial phase, where $\nu$ is the barrier parameter and $\varepsilon$ is a desired accuracy. Finally, our framework allows errors in the calculation of proximal-Newton directions, without sacrificing the worst-case iteration complexity. We demonstrate the merits of our algorithm via three numerical examples, where proximal operators play a key role.

Extended Gauss-Newton and Gauss-Newton-ADMM Algorithms for Low-Rank Matrix Optimization

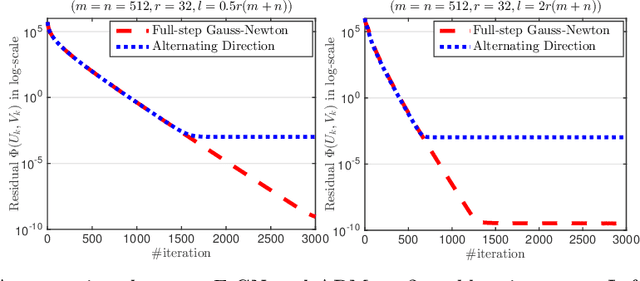
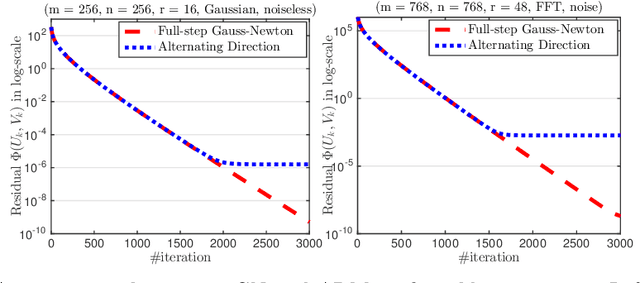
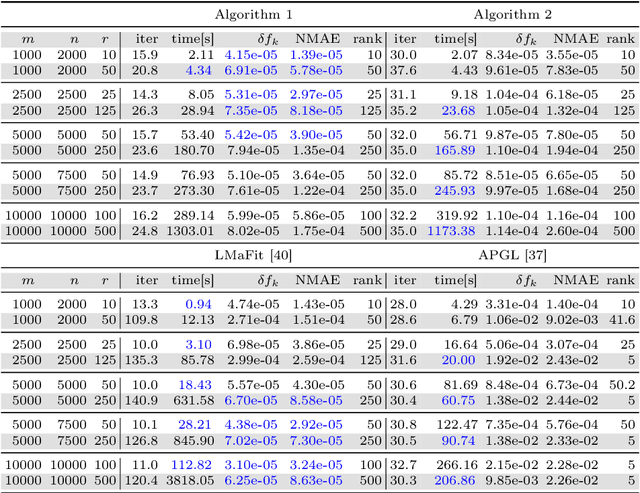
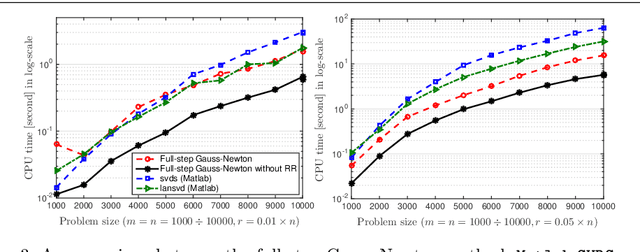
We develop a generic Gauss-Newton (GN) framework for solving a class of nonconvex optimization problems involving low-rank matrix variables. As opposed to standard Gauss-Newton method, our framework allows one to handle general smooth convex cost function via its surrogate. The main complexity-per-iteration consists of the inverse of two rank-size matrices and at most six small matrix multiplications to compute a closed form Gauss-Newton direction, and a backtracking linesearch. We show, under mild conditions, that the proposed algorithm globally and locally converges to a stationary point of the original nonconvex problem. We also show empirically that the Gauss-Newton algorithm achieves much higher accurate solutions compared to the well studied alternating direction method (ADM). Then, we specify our Gauss-Newton framework to handle the symmetric case and prove its convergence, where ADM is not applicable without lifting variables. Next, we incorporate our Gauss-Newton scheme into the alternating direction method of multipliers (ADMM) to design a GN-ADMM algorithm for solving the low-rank optimization problem. We prove that, under mild conditions and a proper choice of the penalty parameter, our GN-ADMM globally converges to a stationary point of the original problem. Finally, we apply our algorithms to solve several problems in practice such as low-rank approximation, matrix completion, robust low-rank matrix recovery, and matrix recovery in quantum tomography. The numerical experiments provide encouraging results to motivate the use of nonconvex optimization.

Adaptive Smoothing Algorithms for Nonsmooth Composite Convex Minimization

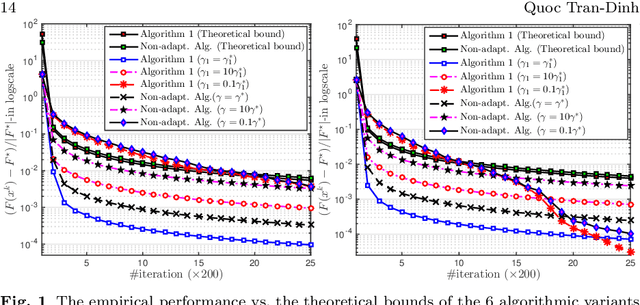
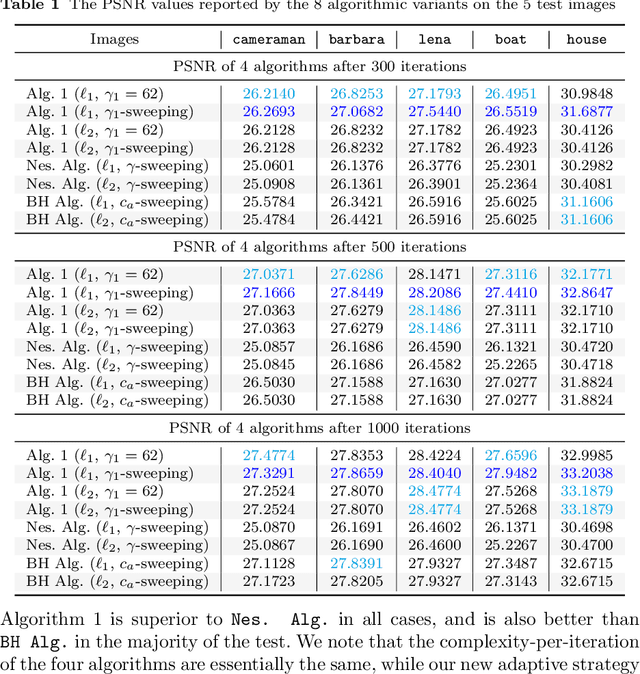
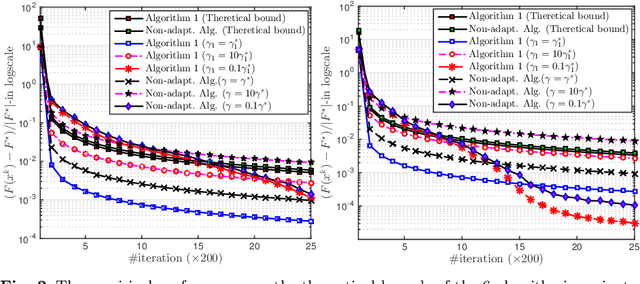
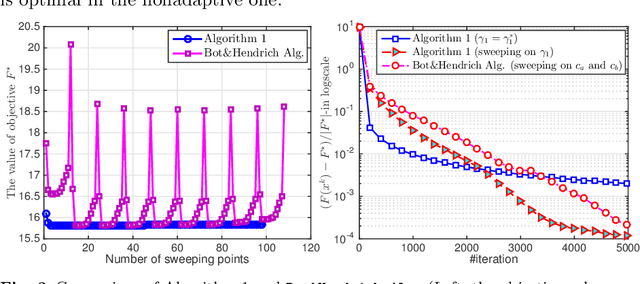
We propose an adaptive smoothing algorithm based on Nesterov's smoothing technique in \cite{Nesterov2005c} for solving "fully" nonsmooth composite convex optimization problems. Our method combines both Nesterov's accelerated proximal gradient scheme and a new homotopy strategy for smoothness parameter. By an appropriate choice of smoothing functions, we develop a new algorithm that has the $\mathcal{O}\left(\frac{1}{\varepsilon}\right)$-worst-case iteration-complexity while preserves the same complexity-per-iteration as in Nesterov's method and allows one to automatically update the smoothness parameter at each iteration. Then, we customize our algorithm to solve four special cases that cover various applications. We also specify our algorithm to solve constrained convex optimization problems and show its convergence guarantee on a primal sequence of iterates. We demonstrate our algorithm through three numerical examples and compare it with other related algorithms.

Convex block-sparse linear regression with expanders -- provably

Sparse matrices are favorable objects in machine learning and optimization. When such matrices are used, in place of dense ones, the overall complexity requirements in optimization can be significantly reduced in practice, both in terms of space and run-time. Prompted by this observation, we study a convex optimization scheme for block-sparse recovery from linear measurements. To obtain linear sketches, we use expander matrices, i.e., sparse matrices containing only few non-zeros per column. Hitherto, to the best of our knowledge, such algorithmic solutions have been only studied from a non-convex perspective. Our aim here is to theoretically characterize the performance of convex approaches under such setting. Our key novelty is the expression of the recovery error in terms of the model-based norm, while assuring that solution lives in the model. To achieve this, we show that sparse model-based matrices satisfy a group version of the null-space property. Our experimental findings on synthetic and real applications support our claims for faster recovery in the convex setting -- as opposed to using dense sensing matrices, while showing a competitive recovery performance.

Structured Sparsity: Discrete and Convex approaches

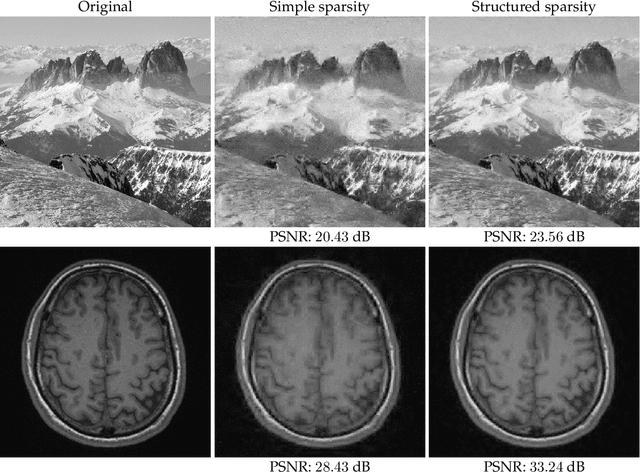
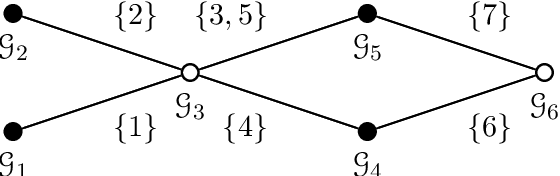
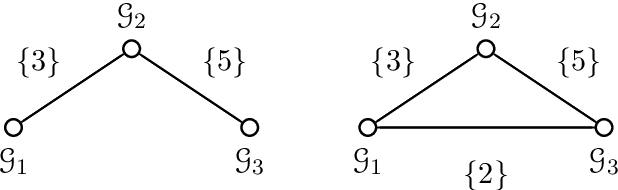
Compressive sensing (CS) exploits sparsity to recover sparse or compressible signals from dimensionality reducing, non-adaptive sensing mechanisms. Sparsity is also used to enhance interpretability in machine learning and statistics applications: While the ambient dimension is vast in modern data analysis problems, the relevant information therein typically resides in a much lower dimensional space. However, many solutions proposed nowadays do not leverage the true underlying structure. Recent results in CS extend the simple sparsity idea to more sophisticated {\em structured} sparsity models, which describe the interdependency between the nonzero components of a signal, allowing to increase the interpretability of the results and lead to better recovery performance. In order to better understand the impact of structured sparsity, in this chapter we analyze the connections between the discrete models and their convex relaxations, highlighting their relative advantages. We start with the general group sparse model and then elaborate on two important special cases: the dispersive and the hierarchical models. For each, we present the models in their discrete nature, discuss how to solve the ensuing discrete problems and then describe convex relaxations. We also consider more general structures as defined by set functions and present their convex proxies. Further, we discuss efficient optimization solutions for structured sparsity problems and illustrate structured sparsity in action via three applications.

A Primal-Dual Algorithmic Framework for Constrained Convex Minimization

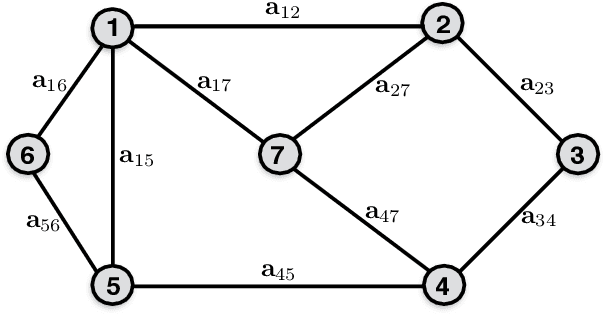
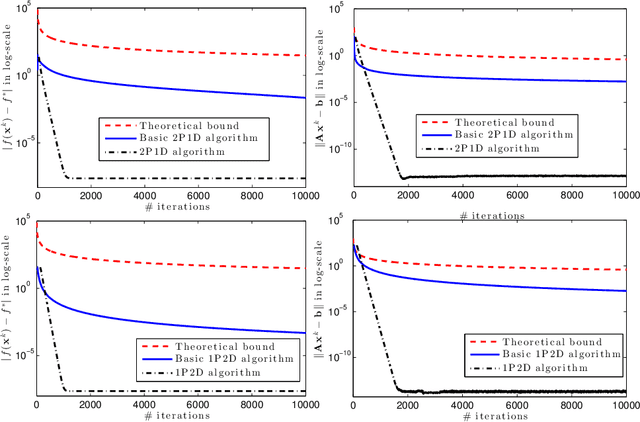
We present a primal-dual algorithmic framework to obtain approximate solutions to a prototypical constrained convex optimization problem, and rigorously characterize how common structural assumptions affect the numerical efficiency. Our main analysis technique provides a fresh perspective on Nesterov's excessive gap technique in a structured fashion and unifies it with smoothing and primal-dual methods. For instance, through the choices of a dual smoothing strategy and a center point, our framework subsumes decomposition algorithms, augmented Lagrangian as well as the alternating direction method-of-multipliers methods as its special cases, and provides optimal convergence rates on the primal objective residual as well as the primal feasibility gap of the iterates for all.

Scalable sparse covariance estimation via self-concordance

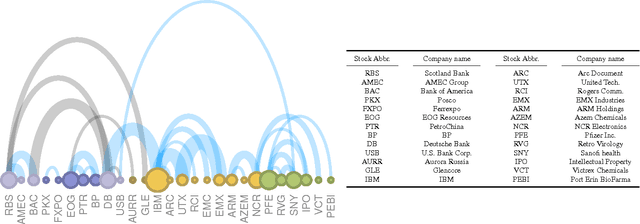
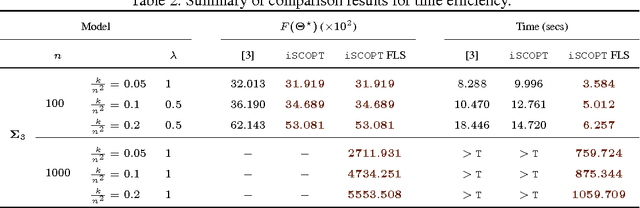
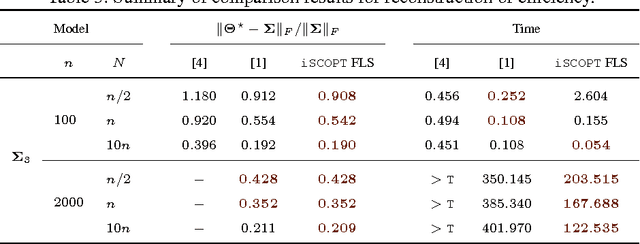
We consider the class of convex minimization problems, composed of a self-concordant function, such as the $\log\det$ metric, a convex data fidelity term $h(\cdot)$ and, a regularizing -- possibly non-smooth -- function $g(\cdot)$. This type of problems have recently attracted a great deal of interest, mainly due to their omnipresence in top-notch applications. Under this \emph{locally} Lipschitz continuous gradient setting, we analyze the convergence behavior of proximal Newton schemes with the added twist of a probable presence of inexact evaluations. We prove attractive convergence rate guarantees and enhance state-of-the-art optimization schemes to accommodate such developments. Experimental results on sparse covariance estimation show the merits of our algorithm, both in terms of recovery efficiency and complexity.

Composite Self-Concordant Minimization

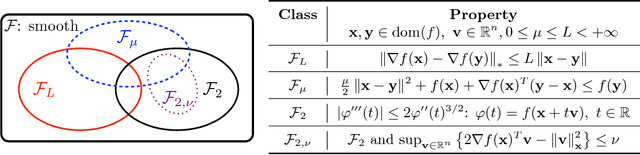
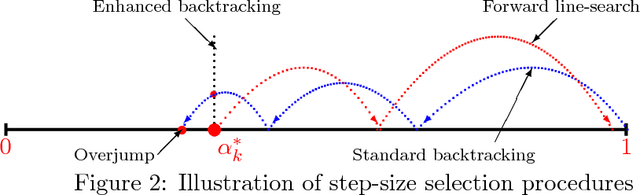
We propose a variable metric framework for minimizing the sum of a self-concordant function and a possibly non-smooth convex function, endowed with an easily computable proximal operator. We theoretically establish the convergence of our framework without relying on the usual Lipschitz gradient assumption on the smooth part. An important highlight of our work is a new set of analytic step-size selection and correction procedures based on the structure of the problem. We describe concrete algorithmic instances of our framework for several interesting applications and demonstrate them numerically on both synthetic and real data.