Halpern-Type Accelerated and Splitting Algorithms For Monotone Inclusions

In this paper, we develop a new type of accelerated algorithms to solve some classes of maximally monotone equations as well as monotone inclusions. Instead of using Nesterov's accelerating approach, our methods rely on a so-called Halpern-type fixed-point iteration in [32], and recently exploited by a number of researchers, including [24, 70]. Firstly, we derive a new variant of the anchored extra-gradient scheme in [70] based on Popov's past extra-gradient method to solve a maximally monotone equation $G(x) = 0$. We show that our method achieves the same $\mathcal{O}(1/k)$ convergence rate (up to a constant factor) as in the anchored extra-gradient algorithm on the operator norm $\Vert G(x_k)\Vert$, , but requires only one evaluation of $G$ at each iteration, where $k$ is the iteration counter. Next, we develop two splitting algorithms to approximate a zero point of the sum of two maximally monotone operators. The first algorithm originates from the anchored extra-gradient method combining with a splitting technique, while the second one is its Popov's variant which can reduce the per-iteration complexity. Both algorithms appear to be new and can be viewed as accelerated variants of the Douglas-Rachford (DR) splitting method. They both achieve $\mathcal{O}(1/k)$ rates on the norm $\Vert G_{\gamma}(x_k)\Vert$ of the forward-backward residual operator $G_{\gamma}(\cdot)$ associated with the problem. We also propose a new accelerated Douglas-Rachford splitting scheme for solving this problem which achieves $\mathcal{O}(1/k)$ convergence rate on $\Vert G_{\gamma}(x_k)\Vert$ under only maximally monotone assumptions. Finally, we specify our first algorithm to solve convex-concave minimax problems and apply our accelerated DR scheme to derive a new variant of the alternating direction method of multipliers (ADMM).

Federated Learning with Randomized Douglas-Rachford Splitting Methods

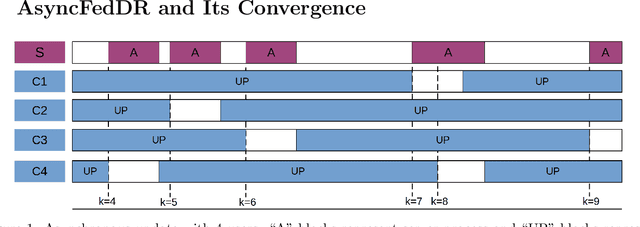
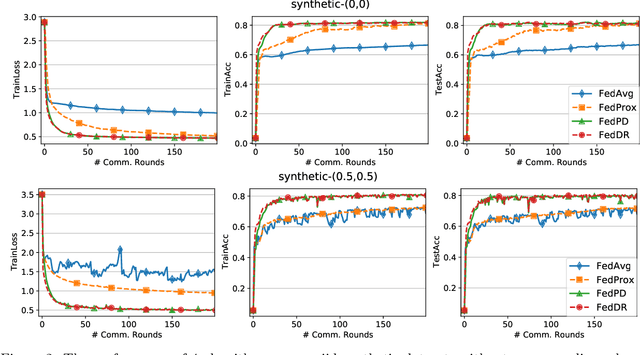
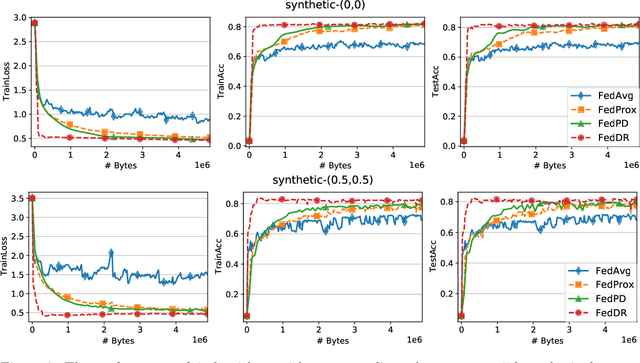
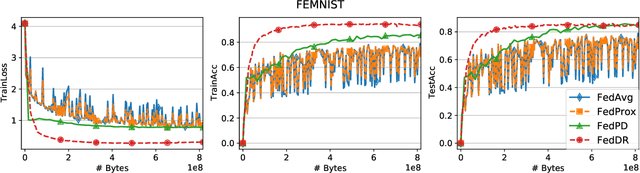
In this paper, we develop two new algorithms, called, \textbf{FedDR} and \textbf{asyncFedDR}, for solving a fundamental nonconvex optimization problem in federated learning. Our algorithms rely on a novel combination between a nonconvex Douglas-Rachford splitting method, randomized block-coordinate strategies, and asynchronous implementation. Unlike recent methods in the literature, e.g., FedSplit and FedPD, our algorithms update only a subset of users at each communication round, and possibly in an asynchronous mode, making them more practical. These new algorithms also achieve communication efficiency and more importantly can handle statistical and system heterogeneity, which are the two main challenges in federated learning. Our convergence analysis shows that the new algorithms match the communication complexity lower bound up to a constant factor under standard assumptions. Our numerical experiments illustrate the advantages of the proposed methods compared to existing ones using both synthetic and real datasets.

Shuffling Gradient-Based Methods with Momentum

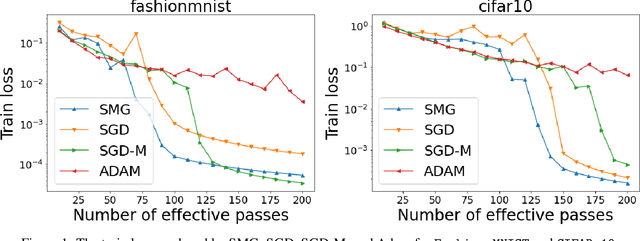
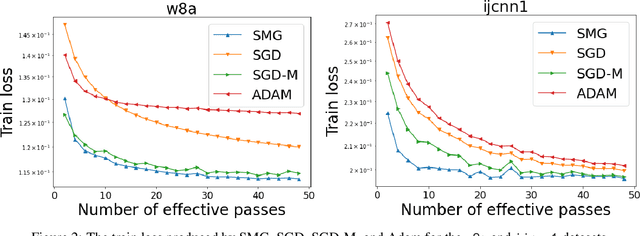
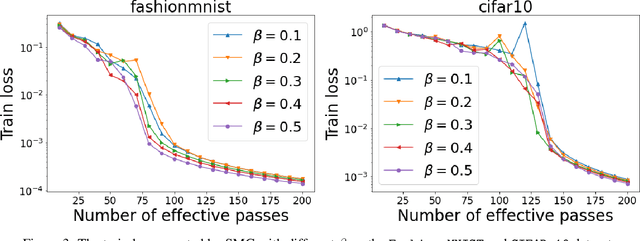
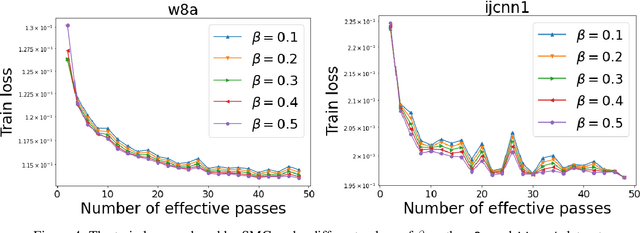
We combine two advanced ideas widely used in optimization for machine learning: shuffling strategy and momentum technique to develop a novel shuffling gradient-based method with momentum to approximate a stationary point of non-convex finite-sum minimization problems. While our method is inspired by momentum techniques, its update is significantly different from existing momentum-based methods. We establish that our algorithm achieves a state-of-the-art convergence rate for both constant and diminishing learning rates under standard assumptions (i.e., $L$-smoothness and bounded variance). When the shuffling strategy is fixed, we develop another new algorithm that is similar to existing momentum methods. This algorithm covers the single-shuffling and incremental gradient schemes as special cases. We prove the same convergence rate of this algorithm under the $L$-smoothness and bounded gradient assumptions. We demonstrate our algorithms via numerical simulations on standard datasets and compare them with existing shuffling methods. Our tests have shown encouraging performance of the new algorithms.

Convergence Analysis of Homotopy-SGD for non-convex optimization

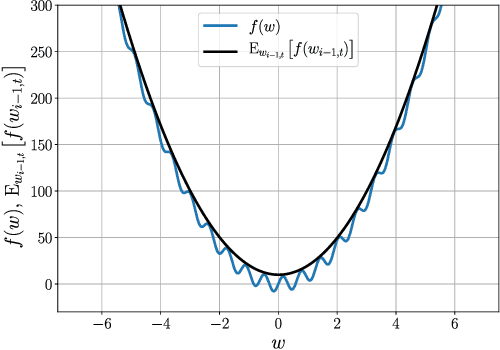
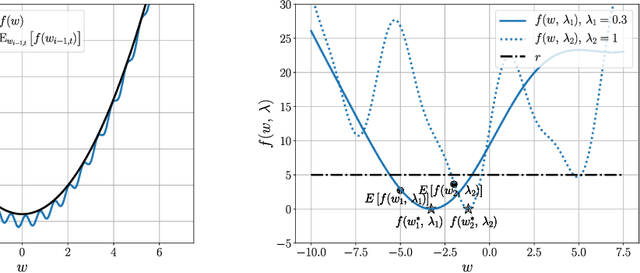
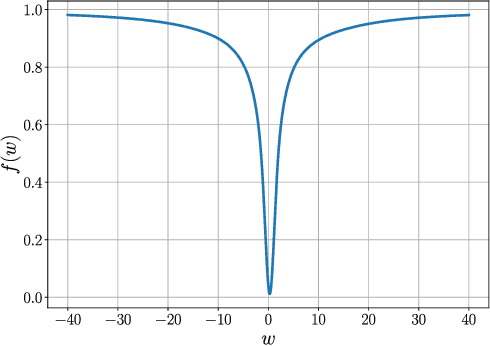
First-order stochastic methods for solving large-scale non-convex optimization problems are widely used in many big-data applications, e.g. training deep neural networks as well as other complex and potentially non-convex machine learning models. Their inexpensive iterations generally come together with slow global convergence rate (mostly sublinear), leading to the necessity of carrying out a very high number of iterations before the iterates reach a neighborhood of a minimizer. In this work, we present a first-order stochastic algorithm based on a combination of homotopy methods and SGD, called Homotopy-Stochastic Gradient Descent (H-SGD), which finds interesting connections with some proposed heuristics in the literature, e.g. optimization by Gaussian continuation, training by diffusion, mollifying networks. Under some mild assumptions on the problem structure, we conduct a theoretical analysis of the proposed algorithm. Our analysis shows that, with a specifically designed scheme for the homotopy parameter, H-SGD enjoys a global linear rate of convergence to a neighborhood of a minimum while maintaining fast and inexpensive iterations. Experimental evaluations confirm the theoretical results and show that H-SGD can outperform standard SGD.

Hogwild! over Distributed Local Data Sets with Linearly Increasing Mini-Batch Sizes

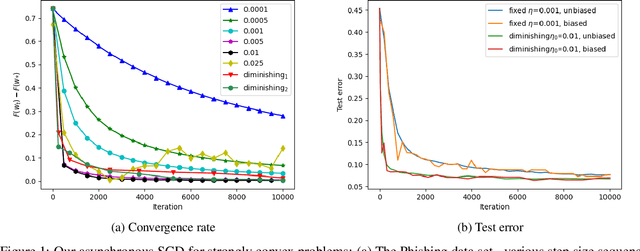
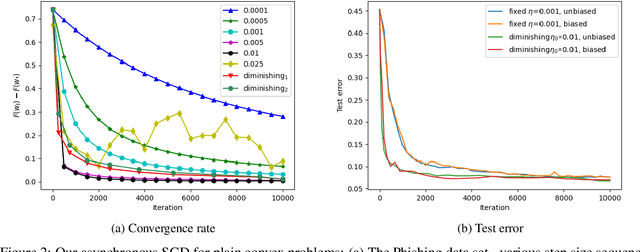
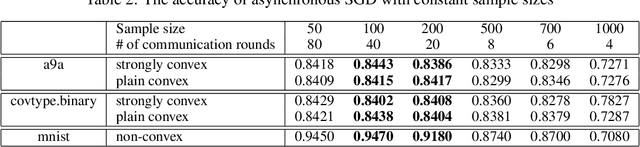
Hogwild! implements asynchronous Stochastic Gradient Descent (SGD) where multiple threads in parallel access a common repository containing training data, perform SGD iterations and update shared state that represents a jointly learned (global) model. We consider big data analysis where training data is distributed among local data sets -- and we wish to move SGD computations to local compute nodes where local data resides. The results of these local SGD computations are aggregated by a central "aggregator" which mimics Hogwild!. We show how local compute nodes can start choosing small mini-batch sizes which increase to larger ones in order to reduce communication cost (round interaction with the aggregator). We prove a tight and novel non-trivial convergence analysis for strongly convex problems which does not use the bounded gradient assumption as seen in many existing publications. The tightness is a consequence of our proofs for lower and upper bounds of the convergence rate, which show a constant factor difference. We show experimental results for plain convex and non-convex problems for biased and unbiased local data sets.

An Optimal Hybrid Variance-Reduced Algorithm for Stochastic Composite Nonconvex Optimization

In this note we propose a new variant of the hybrid variance-reduced proximal gradient method in [7] to solve a common stochastic composite nonconvex optimization problem under standard assumptions. We simply replace the independent unbiased estimator in our hybrid- SARAH estimator introduced in [7] by the stochastic gradient evaluated at the same sample, leading to the identical momentum-SARAH estimator introduced in [2]. This allows us to save one stochastic gradient per iteration compared to [7], and only requires two samples per iteration. Our algorithm is very simple and achieves optimal stochastic oracle complexity bound in terms of stochastic gradient evaluations (up to a constant factor). Our analysis is essentially inspired by [7], but we do not use two different step-sizes.

Asynchronous Federated Learning with Reduced Number of Rounds and with Differential Privacy from Less Aggregated Gaussian Noise

The feasibility of federated learning is highly constrained by the server-clients infrastructure in terms of network communication. Most newly launched smartphones and IoT devices are equipped with GPUs or sufficient computing hardware to run powerful AI models. However, in case of the original synchronous federated learning, client devices suffer waiting times and regular communication between clients and server is required. This implies more sensitivity to local model training times and irregular or missed updates, hence, less or limited scalability to large numbers of clients and convergence rates measured in real time will suffer. We propose a new algorithm for asynchronous federated learning which eliminates waiting times and reduces overall network communication - we provide rigorous theoretical analysis for strongly convex objective functions and provide simulation results. By adding Gaussian noise we show how our algorithm can be made differentially private -- new theorems show how the aggregated added Gaussian noise is significantly reduced.

Hybrid Variance-Reduced SGD Algorithms For Nonconvex-Concave Minimax Problems

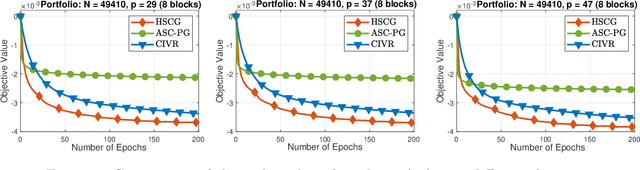
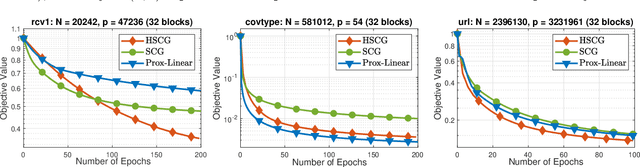
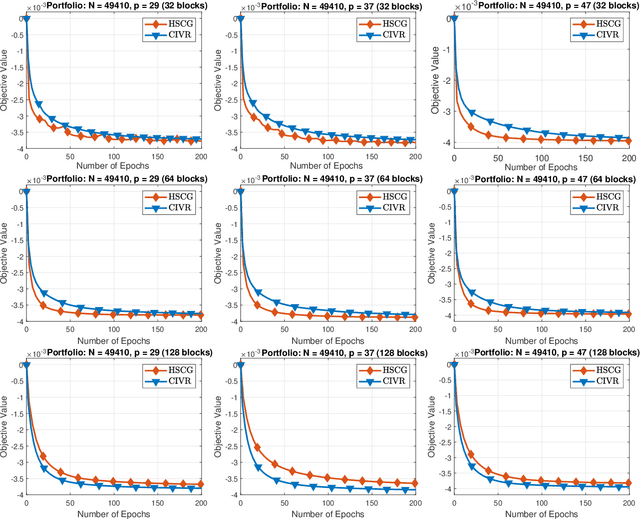
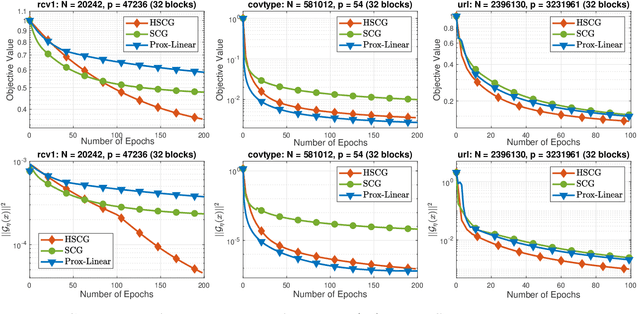
We develop a novel variance-reduced algorithm to solve a stochastic nonconvex-concave minimax problem which has various applications in different fields. This problem has several computational challenges due to its nonsmoothness, nonconvexity, nonlinearity, and non-separability of the objective functions. Our approach relies on a novel combination of recent ideas, including smoothing and hybrid stochastic variance-reduced techniques. Our algorithm and its variants can achieve $\mathcal{O}(T^{-2/3})$-convergence rate in $T$, and the best-known oracle complexity under standard assumptions. They have several computational advantages compared to existing methods. They can also work with both single sample or mini-batch on derivative estimators, with constant or diminishing step-sizes. We demonstrate the benefits of our algorithms over existing methods through two numerical examples.

Randomized Primal-Dual Algorithms for Composite Convex Minimization with Faster Convergence Rates

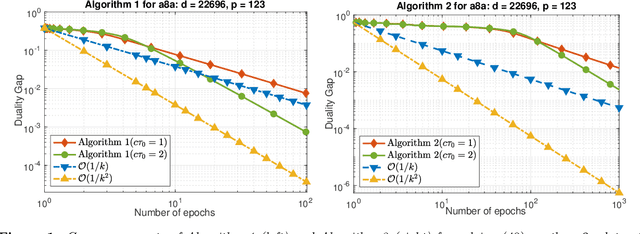
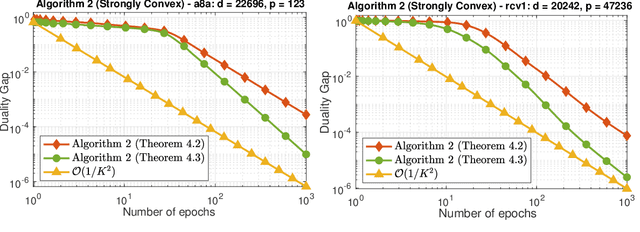
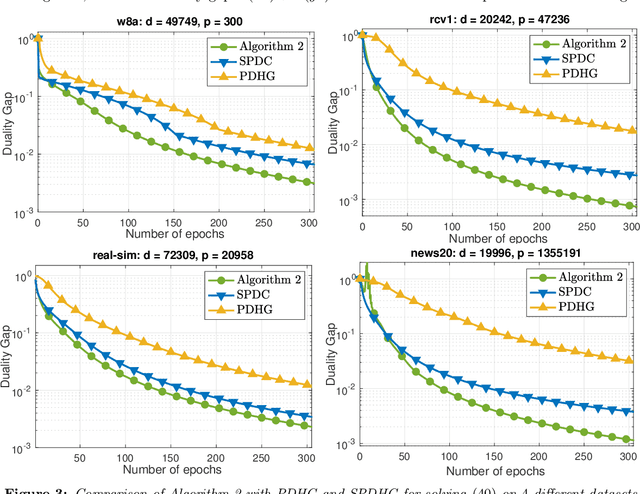
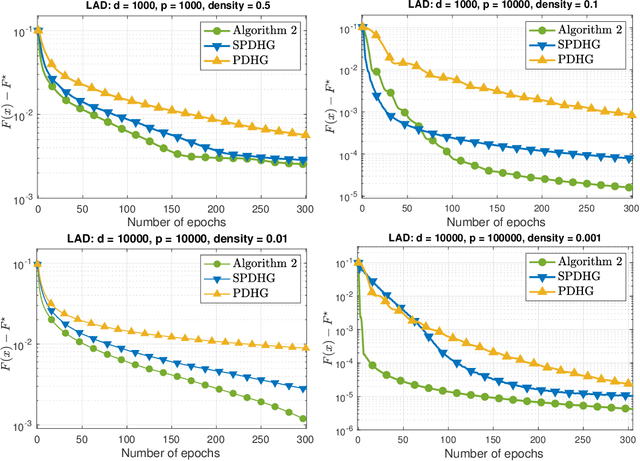
We develop two novel randomized primal-dual algorithms to solve nonsmooth composite convex optimization problems. The first algorithm is fully randomized, i.e., it has randomized updates on both primal and dual variables, while the second one is a semi-randomized scheme which only has one randomized update on the primal (or dual) variable while using the full update for the other. Both algorithms achieve the best-known $\mathcal{O}(1/k)$ or $\mathcal{O}(1/k^2)$ convergence rates in expectation under either only convexity or strong convexity, respectively, where $k$ is the iteration counter. Interestingly, with new parameter update rules, our algorithms can achieve $o(1/k)$ or $o(1/k^2)$ best-iterate convergence rate in expectation under either convexity or strong convexity, respectively. These rates can be obtained for both the primal and dual problems. To the best of our knowledge, this is the first time such faster convergence rates are shown for randomized primal-dual methods. Finally, we verify our theoretical results via two numerical examples and compare them with the state-of-the-art.

A Hybrid Stochastic Policy Gradient Algorithm for Reinforcement Learning

We propose a novel hybrid stochastic policy gradient estimator by combining an unbiased policy gradient estimator, the REINFORCE estimator, with another biased one, an adapted SARAH estimator for policy optimization. The hybrid policy gradient estimator is shown to be biased, but has variance reduced property. Using this estimator, we develop a new Proximal Hybrid Stochastic Policy Gradient Algorithm (ProxHSPGA) to solve a composite policy optimization problem that allows us to handle constraints or regularizers on the policy parameters. We first propose a single-looped algorithm then introduce a more practical restarting variant. We prove that both algorithms can achieve the best-known trajectory complexity $\mathcal{O}\left(\varepsilon^{-3}\right)$ to attain a first-order stationary point for the composite problem which is better than existing REINFORCE/GPOMDP $\mathcal{O}\left(\varepsilon^{-4}\right)$ and SVRPG $\mathcal{O}\left(\varepsilon^{-10/3}\right)$ in the non-composite setting. We evaluate the performance of our algorithm on several well-known examples in reinforcement learning. Numerical results show that our algorithm outperforms two existing methods on these examples. Moreover, the composite settings indeed have some advantages compared to the non-composite ones on certain problems.