Financial Fraud Detection using Jump-Attentive Graph Neural Networks

As the availability of financial services online continues to grow, the incidence of fraud has surged correspondingly. Fraudsters continually seek new and innovative ways to circumvent the detection algorithms in place. Traditionally, fraud detection relied on rule-based methods, where rules were manually created based on transaction data features. However, these techniques soon became ineffective due to their reliance on manual rule creation and their inability to detect complex data patterns. Today, a significant portion of the financial services sector employs various machine learning algorithms, such as XGBoost, Random Forest, and neural networks, to model transaction data. While these techniques have proven more efficient than rule-based methods, they still fail to capture interactions between different transactions and their interrelationships. Recently, graph-based techniques have been adopted for financial fraud detection, leveraging graph topology to aggregate neighborhood information of transaction data using Graph Neural Networks (GNNs). Despite showing improvements over previous methods, these techniques still struggle to keep pace with the evolving camouflaging tactics of fraudsters and suffer from information loss due to over-smoothing. In this paper, we propose a novel algorithm that employs an efficient neighborhood sampling method, effective for camouflage detection and preserving crucial feature information from non-similar nodes. Additionally, we introduce a novel GNN architecture that utilizes attention mechanisms and preserves holistic neighborhood information to prevent information loss. We test our algorithm on financial data to show that our method outperforms other state-of-the-art graph algorithms.

Enhancing Financial Fraud Detection with Human-in-the-Loop Feedback and Feedback Propagation

Human-in-the-loop (HITL) feedback mechanisms can significantly enhance machine learning models, particularly in financial fraud detection, where fraud patterns change rapidly, and fraudulent nodes are sparse. Even small amounts of feedback from Subject Matter Experts (SMEs) can notably boost model performance. This paper examines the impact of HITL feedback on both traditional and advanced techniques using proprietary and publicly available datasets. Our results show that HITL feedback improves model accuracy, with graph-based techniques benefiting the most. We also introduce a novel feedback propagation method that extends feedback across the dataset, further enhancing detection accuracy. By leveraging human expertise, this approach addresses challenges related to evolving fraud patterns, data sparsity, and model interpretability, ultimately improving model robustness and streamlining the annotation process.

GPT-Guided Monte Carlo Tree Search for Symbolic Regression in Financial Fraud Detection

With the increasing number of financial services available online, the rate of financial fraud has also been increasing. The traffic and transaction rates on the internet have increased considerably, leading to a need for fast decision-making. Financial institutions also have stringent regulations that often require transparency and explainability of the decision-making process. However, most state-of-the-art algorithms currently used in the industry are highly parameterized black-box models that rely on complex computations to generate a score. These algorithms are inherently slow and lack the explainability and speed of traditional rule-based learners. This work introduces SR-MCTS (Symbolic Regression MCTS), which utilizes a foundational GPT model to guide the MCTS, significantly enhancing its convergence speed and the quality of the generated expressions which are further extracted to rules. Our experiments show that SR-MCTS can detect fraud more efficiently than widely used methods in the industry while providing substantial insights into the decision-making process.

Dual Monte Carlo Tree Search

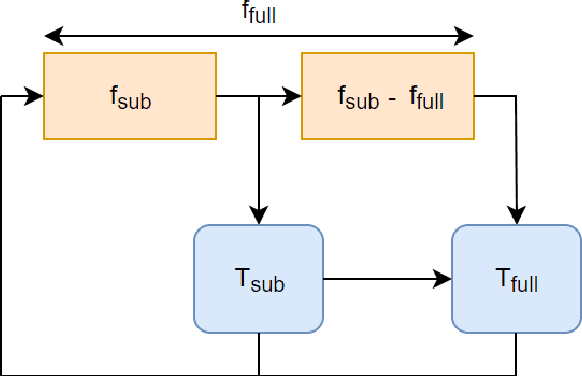
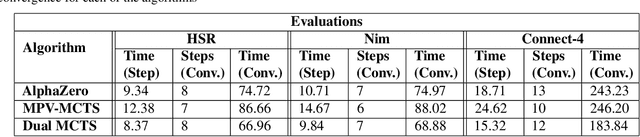
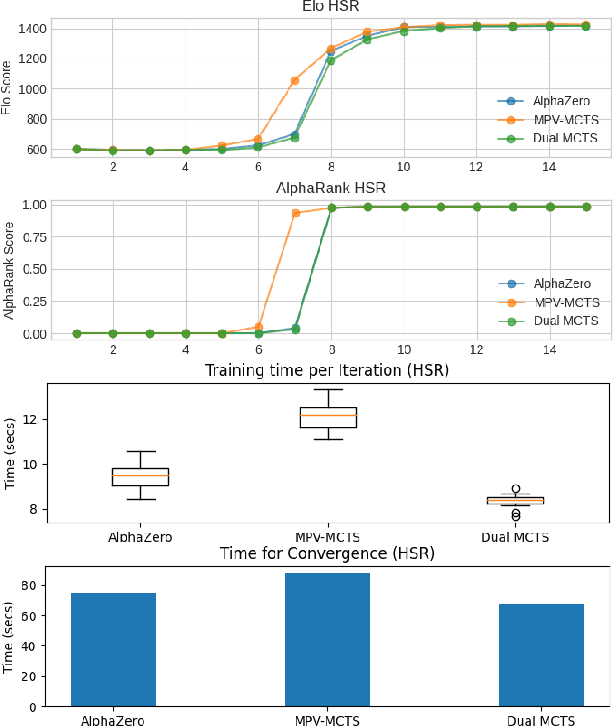
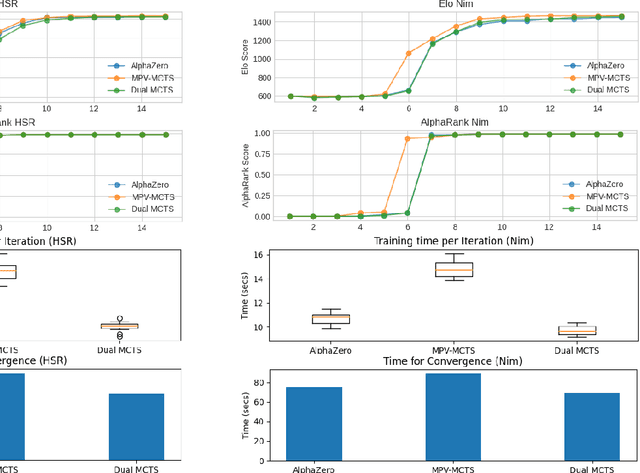
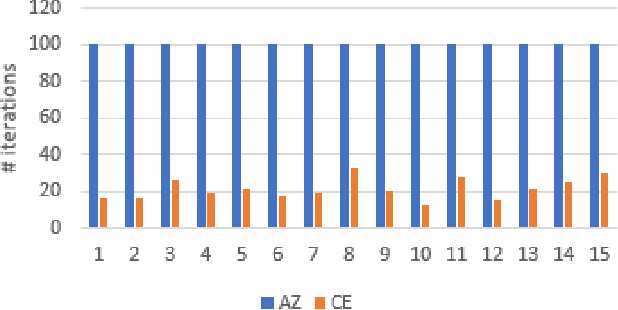
AlphaZero, using a combination of Deep Neural Networks and Monte Carlo Tree Search (MCTS), has successfully trained reinforcement learning agents in a tabula-rasa way. The neural MCTS algorithm has been successful in finding near-optimal strategies for games through self-play. However, the AlphaZero algorithm has a significant drawback; it takes a long time to converge and requires high computational power due to complex neural networks for solving games like Chess, Go, Shogi, etc. Owing to this, it is very difficult to pursue neural MCTS research without cutting-edge hardware, which is a roadblock for many aspiring neural MCTS researchers. In this paper, we propose a new neural MCTS algorithm, called Dual MCTS, which helps overcome these drawbacks. Dual MCTS uses two different search trees, a single deep neural network, and a new update technique for the search trees using a combination of the PUCB, a sliding-window, and the epsilon-greedy algorithm. This technique is applicable to any MCTS based algorithm to reduce the number of updates to the tree. We show that Dual MCTS performs better than one of the most widely used neural MCTS algorithms, AlphaZero, for various symmetric and asymmetric games.

First-Order Problem Solving through Neural MCTS based Reinforcement Learning

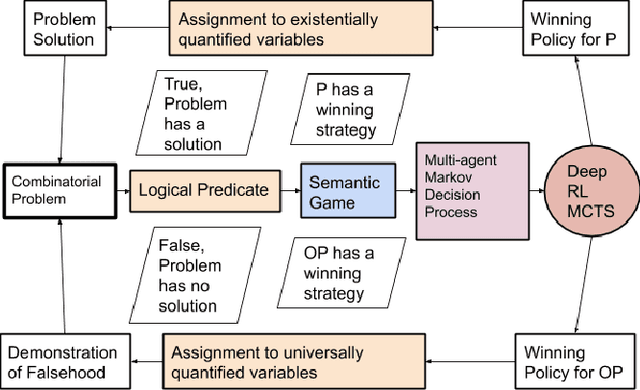
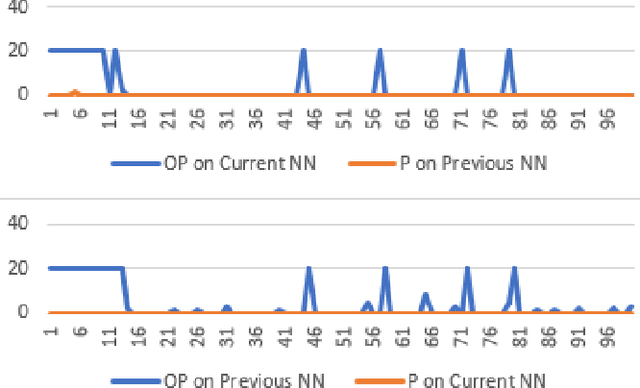
The formal semantics of an interpreted first-order logic (FOL) statement can be given in Tarskian Semantics or a basically equivalent Game Semantics. The latter maps the statement and the interpretation into a two-player semantic game. Many combinatorial problems can be described using interpreted FOL statements and can be mapped into a semantic game. Therefore, learning to play a semantic game perfectly leads to the solution of a specific instance of a combinatorial problem. We adapt the AlphaZero algorithm so that it becomes better at learning to play semantic games that have different characteristics than Go and Chess. We propose a general framework, Persephone, to map the FOL description of a combinatorial problem to a semantic game so that it can be solved through a neural MCTS based reinforcement learning algorithm. Our goal for Persephone is to make it tabula-rasa, mapping a problem stated in interpreted FOL to a solution without human intervention.