KO codes: Inventing Nonlinear Encoding and Decoding for Reliable Wireless Communication via Deep-learning

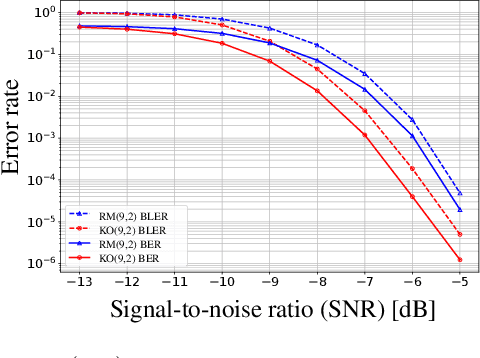
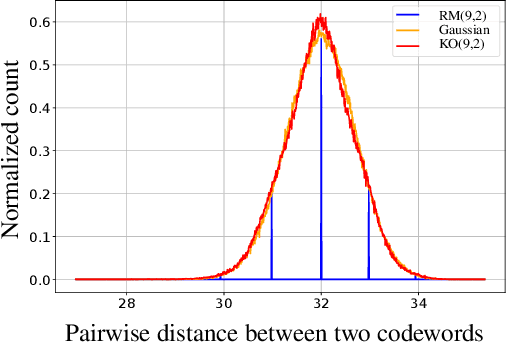
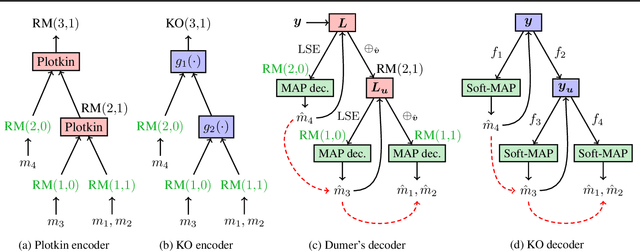
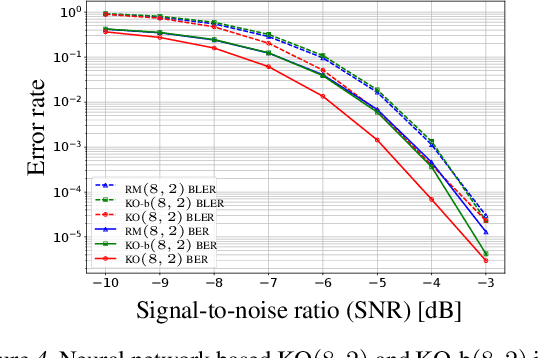
Landmark codes underpin reliable physical layer communication, e.g., Reed-Muller, BCH, Convolution, Turbo, LDPC and Polar codes: each is a linear code and represents a mathematical breakthrough. The impact on humanity is huge: each of these codes has been used in global wireless communication standards (satellite, WiFi, cellular). Reliability of communication over the classical additive white Gaussian noise (AWGN) channel enables benchmarking and ranking of the different codes. In this paper, we construct KO codes, a computationaly efficient family of deep-learning driven (encoder, decoder) pairs that outperform the state-of-the-art reliability performance on the standardized AWGN channel. KO codes beat state-of-the-art Reed-Muller and Polar codes, under the low-complexity successive cancellation decoding, in the challenging short-to-medium block length regime on the AWGN channel. We show that the gains of KO codes are primarily due to the nonlinear mapping of information bits directly to transmit real symbols (bypassing modulation) and yet possess an efficient, high performance decoder. The key technical innovation that renders this possible is design of a novel family of neural architectures inspired by the computation tree of the {\bf K}ronecker {\bf O}peration (KO) central to Reed-Muller and Polar codes. These architectures pave way for the discovery of a much richer class of hitherto unexplored nonlinear algebraic structures. The code is available at \href{https://github.com/deepcomm/KOcodes}{https://github.com/deepcomm/KOcodes}

Enriching Word Embeddings with Temporal and Spatial Information

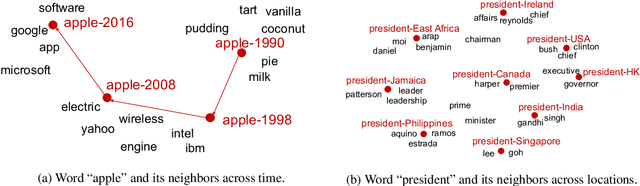
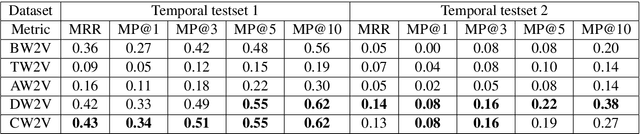
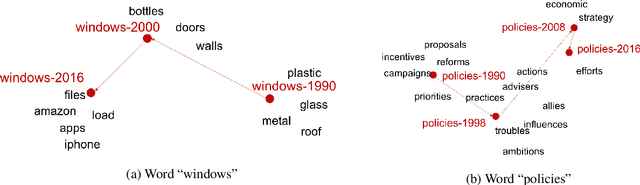
The meaning of a word is closely linked to sociocultural factors that can change over time and location, resulting in corresponding meaning changes. Taking a global view of words and their meanings in a widely used language, such as English, may require us to capture more refined semantics for use in time-specific or location-aware situations, such as the study of cultural trends or language use. However, popular vector representations for words do not adequately include temporal or spatial information. In this work, we present a model for learning word representation conditioned on time and location. In addition to capturing meaning changes over time and location, we require that the resulting word embeddings retain salient semantic and geometric properties. We train our model on time- and location-stamped corpora, and show using both quantitative and qualitative evaluations that it can capture semantics across time and locations. We note that our model compares favorably with the state-of-the-art for time-specific embedding, and serves as a new benchmark for location-specific embeddings.

Deepcode and Modulo-SK are Designed for Different Settings

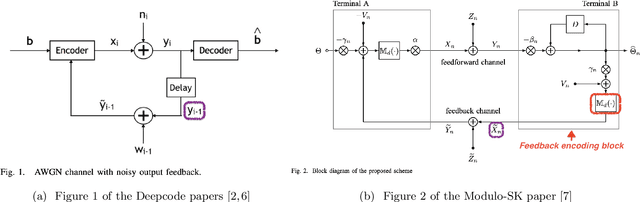
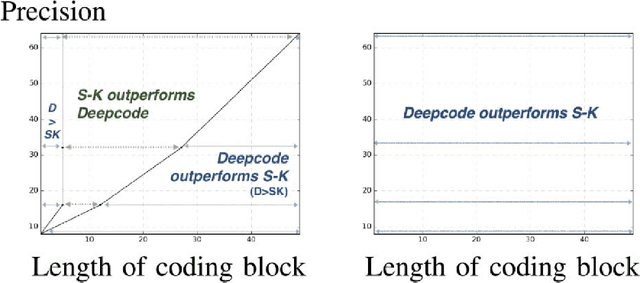
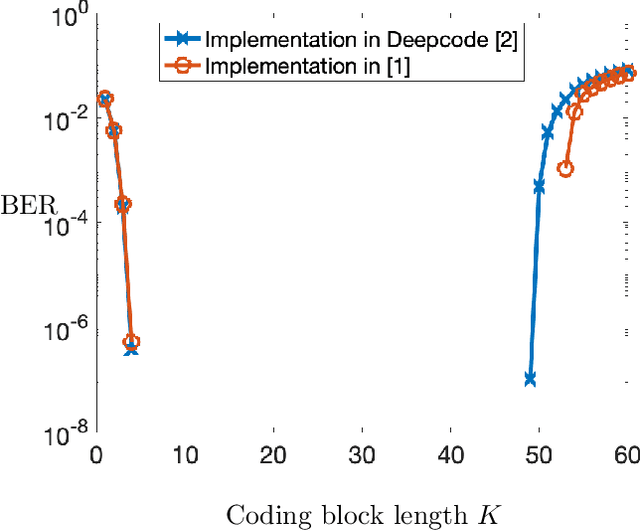
We respond to [1] which claimed that "Modulo-SK scheme outperforms Deepcode [2]". We demonstrate that this statement is not true: the two schemes are designed and evaluated for entirely different settings. DeepCode is designed and evaluated for the AWGN channel with (potentially delayed) uncoded output feedback. Modulo-SK is evaluated on the AWGN channel with coded feedback and unit delay. [1] also claimed an implementation of Schalkwijk and Kailath (SK) [3] which was numerically stable for any number of information bits and iterations. However, we observe that while their implementation does marginally improve over ours, it also suffers from a fundamental issue with precision. Finally, we show that Deepcode dominates the optimized performance of SK, over a natural choice of parameterizations when the feedback is noisy.

Turbo Autoencoder: Deep learning based channel codes for point-to-point communication channels

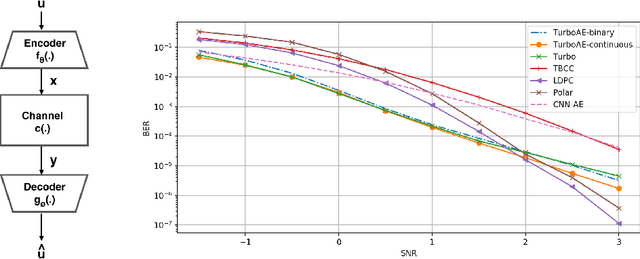
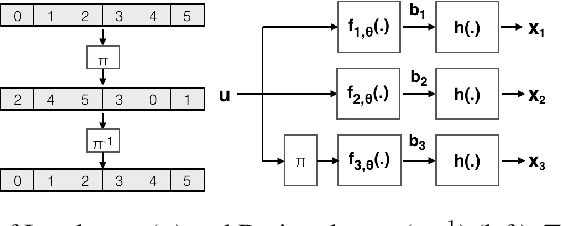
Designing codes that combat the noise in a communication medium has remained a significant area of research in information theory as well as wireless communications. Asymptotically optimal channel codes have been developed by mathematicians for communicating under canonical models after over 60 years of research. On the other hand, in many non-canonical channel settings, optimal codes do not exist and the codes designed for canonical models are adapted via heuristics to these channels and are thus not guaranteed to be optimal. In this work, we make significant progress on this problem by designing a fully end-to-end jointly trained neural encoder and decoder, namely, Turbo Autoencoder (TurboAE), with the following contributions: ($a$) under moderate block lengths, TurboAE approaches state-of-the-art performance under canonical channels; ($b$) moreover, TurboAE outperforms the state-of-the-art codes under non-canonical settings in terms of reliability. TurboAE shows that the development of channel coding design can be automated via deep learning, with near-optimal performance.

Learning in Gated Neural Networks

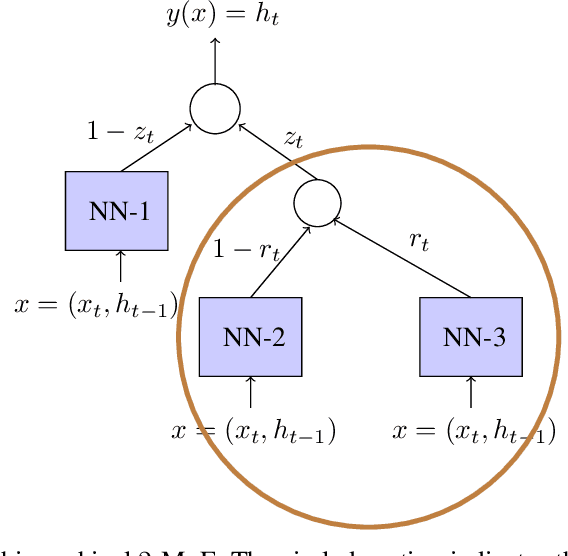
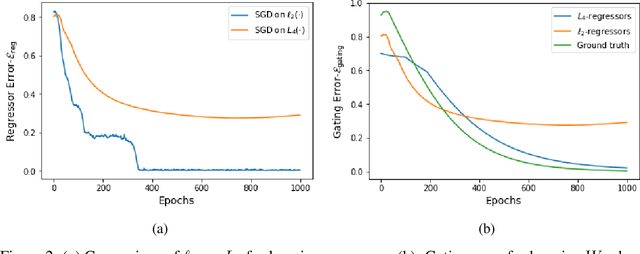
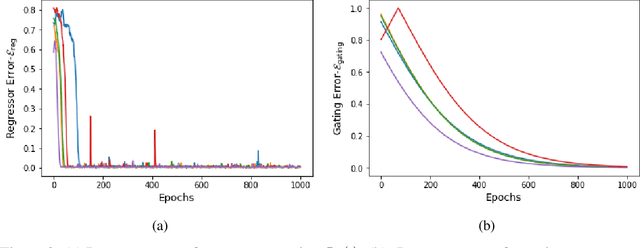
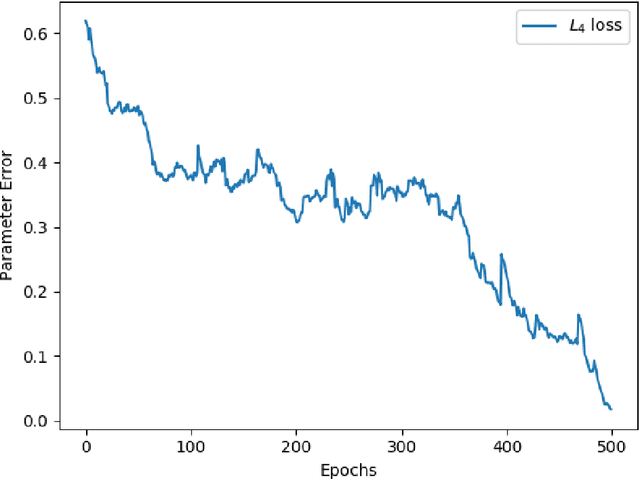
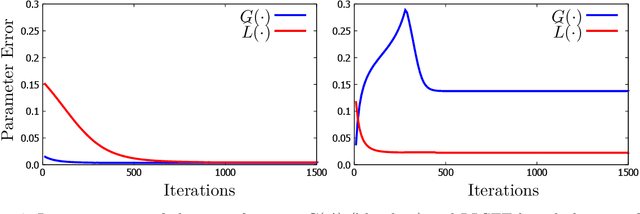
Gating is a key feature in modern neural networks including LSTMs, GRUs and sparsely-gated deep neural networks. The backbone of such gated networks is a mixture-of-experts layer, where several experts make regression decisions and gating controls how to weigh the decisions in an input-dependent manner. Despite having such a prominent role in both modern and classical machine learning, very little is understood about parameter recovery of mixture-of-experts since gradient descent and EM algorithms are known to be stuck in local optima in such models. In this paper, we perform a careful analysis of the optimization landscape and show that with appropriately designed loss functions, gradient descent can indeed learn the parameters accurately. A key idea underpinning our results is the design of two {\em distinct} loss functions, one for recovering the expert parameters and another for recovering the gating parameters. We demonstrate the first sample complexity results for parameter recovery in this model for any algorithm and demonstrate significant performance gains over standard loss functions in numerical experiments.

Context-Sensitive Malicious Spelling Error Correction

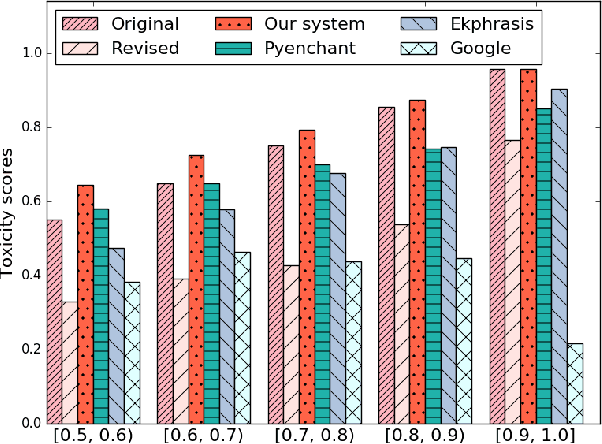
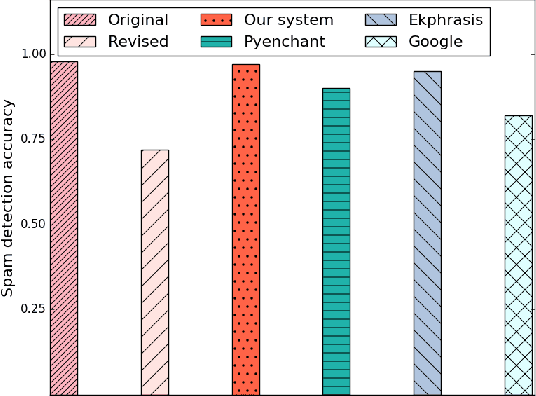
Misspelled words of the malicious kind work by changing specific keywords and are intended to thwart existing automated applications for cyber-environment control such as harassing content detection on the Internet and email spam detection. In this paper, we focus on malicious spelling correction, which requires an approach that relies on the context and the surface forms of targeted keywords. In the context of two applications--profanity detection and email spam detection--we show that malicious misspellings seriously degrade their performance. We then propose a context-sensitive approach for malicious spelling correction using word embeddings and demonstrate its superior performance compared to state-of-the-art spell checkers.

LEARN Codes: Inventing Low-latency Codes via Recurrent Neural Networks

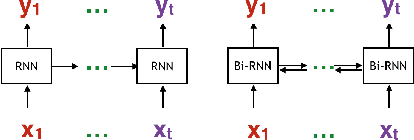
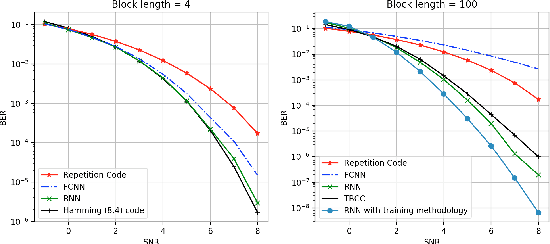
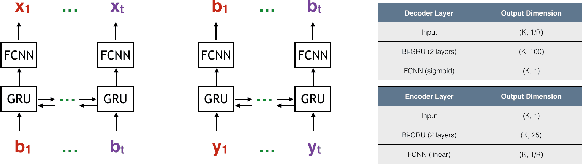
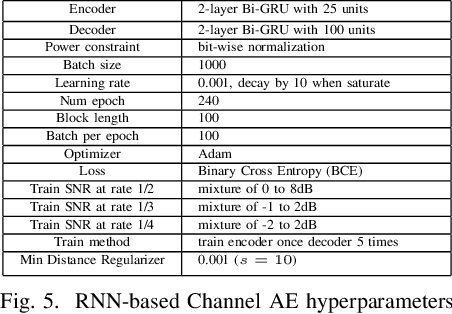
Designing channel codes under low latency constraints is one of the most demanding requirements in 5G standards. However, sharp characterizations of the performances of traditional codes are only available in the large block-length limit. Code designs are guided by those asymptotic analyses and require large block lengths and long latency to achieve the desired error rate. Furthermore, when the codes designed for one channel (e.g. Additive White Gaussian Noise (AWGN) channel) are used for another (e.g. non-AWGN channels), heuristics are necessary to achieve any nontrivial performance -thereby severely lacking in robustness as well as adaptivity. Obtained by jointly designing Recurrent Neural Network (RNN) based encoder and decoder, we propose an end-to-end learned neural code which outperforms canonical convolutional code under block settings. With this gained experience of designing a novel neural block code, we propose a new class of codes under low latency constraint - Low-latency Efficient Adaptive Robust Neural (LEARN) codes, which outperforms the state-of-the-art low latency codes as well as exhibits robustness and adaptivity properties. LEARN codes show the potential of designing new versatile and universal codes for future communications via tools of modern deep learning coupled with communication engineering insights.

Estimating Mutual Information for Discrete-Continuous Mixtures

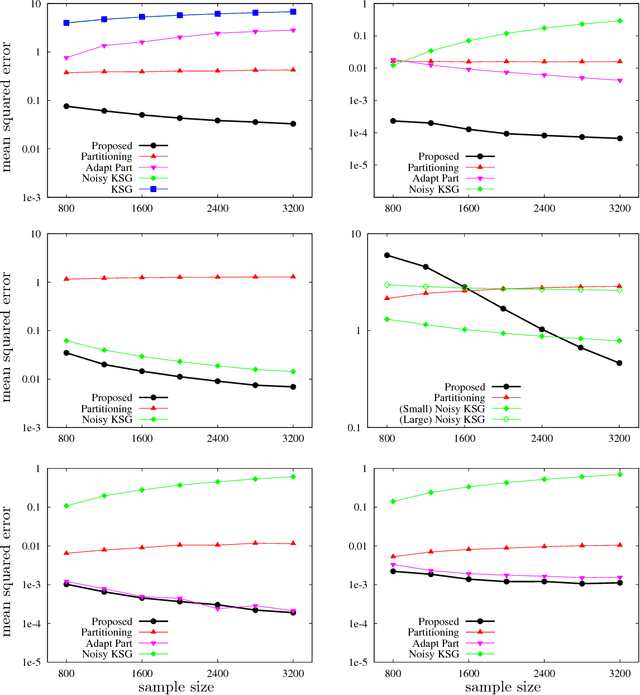
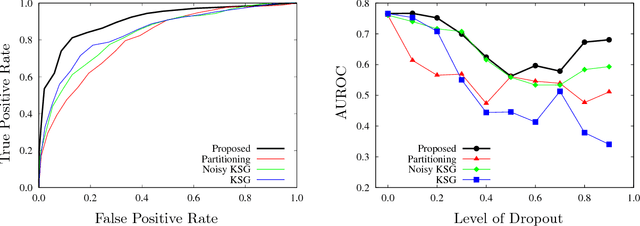
Estimating mutual information from observed samples is a basic primitive, useful in several machine learning tasks including correlation mining, information bottleneck clustering, learning a Chow-Liu tree, and conditional independence testing in (causal) graphical models. While mutual information is a well-defined quantity in general probability spaces, existing estimators can only handle two special cases of purely discrete or purely continuous pairs of random variables. The main challenge is that these methods first estimate the (differential) entropies of X, Y and the pair (X;Y) and add them up with appropriate signs to get an estimate of the mutual information. These 3H-estimators cannot be applied in general mixture spaces, where entropy is not well-defined. In this paper, we design a novel estimator for mutual information of discrete-continuous mixtures. We prove that the proposed estimator is consistent. We provide numerical experiments suggesting superiority of the proposed estimator compared to other heuristics of adding small continuous noise to all the samples and applying standard estimators tailored for purely continuous variables, and quantizing the samples and applying standard estimators tailored for purely discrete variables. This significantly widens the applicability of mutual information estimation in real-world applications, where some variables are discrete, some continuous, and others are a mixture between continuous and discrete components.

Learning One-hidden-layer Neural Networks under General Input Distributions

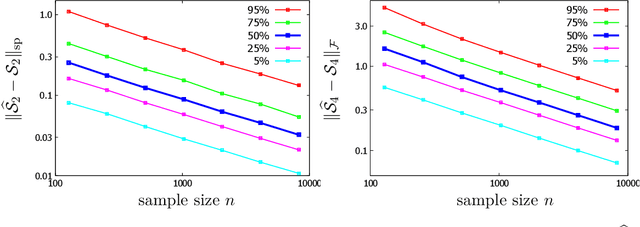
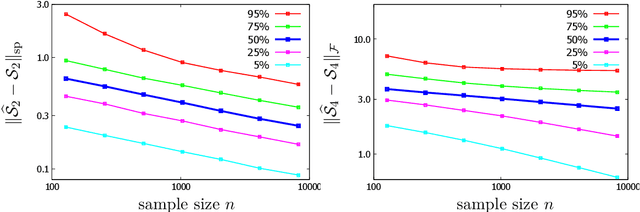
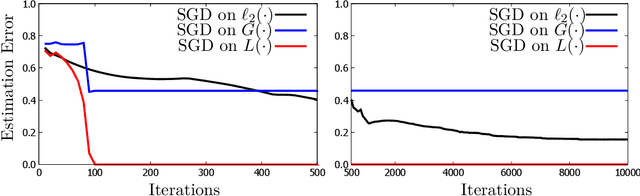
Significant advances have been made recently on training neural networks, where the main challenge is in solving an optimization problem with abundant critical points. However, existing approaches to address this issue crucially rely on a restrictive assumption: the training data is drawn from a Gaussian distribution. In this paper, we provide a novel unified framework to design loss functions with desirable landscape properties for a wide range of general input distributions. On these loss functions, remarkably, stochastic gradient descent theoretically recovers the true parameters with global initializations and empirically outperforms the existing approaches. Our loss function design bridges the notion of score functions with the topic of neural network optimization. Central to our approach is the task of estimating the score function from samples, which is of basic and independent interest to theoretical statistics. Traditional estimation methods (example: kernel based) fail right at the outset; we bring statistical methods of local likelihood to design a novel estimator of score functions, that provably adapts to the local geometry of the unknown density.

Graph2Seq: Scalable Learning Dynamics for Graphs

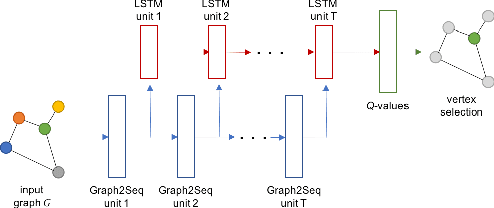
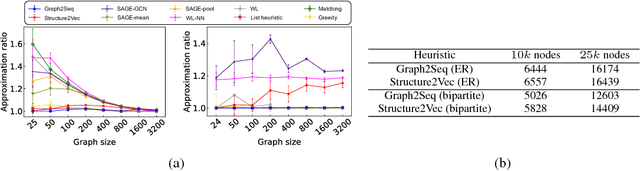
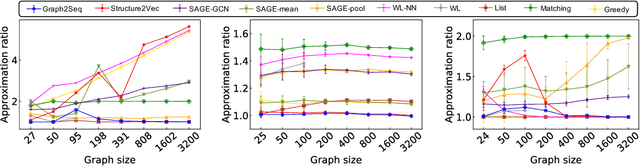
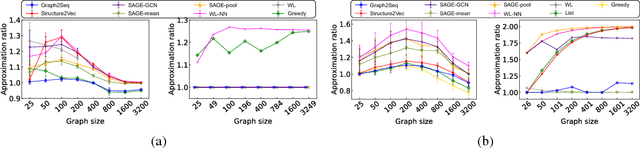
Neural networks have been shown to be an effective tool for learning algorithms over graph-structured data. However, graph representation techniques---that convert graphs to real-valued vectors for use with neural networks---are still in their infancy. Recent works have proposed several approaches (e.g., graph convolutional networks), but these methods have difficulty scaling and generalizing to graphs with different sizes and shapes. We present Graph2Seq, a new technique that represents vertices of graphs as infinite time-series. By not limiting the representation to a fixed dimension, Graph2Seq scales naturally to graphs of arbitrary sizes and shapes. Graph2Seq is also reversible, allowing full recovery of the graph structure from the sequences. By analyzing a formal computational model for graph representation, we show that an unbounded sequence is necessary for scalability. Our experimental results with Graph2Seq show strong generalization and new state-of-the-art performance on a variety of graph combinatorial optimization problems.