Joint Analog Beam Selection and Digital Beamforming in Millimeter Wave Cell-Free Massive MIMO Systems

Cell-free massive MIMO systems consist of many distributed access points with simple components that jointly serve the users. In millimeter wave bands, only a limited set of predetermined beams can be supported. In a network that consolidates these technologies, downlink analog beam selection stands as a challenging task for the network sum-rate maximization. Low-cost digital filters can improve the network sum-rate further. In this work, we propose low-cost joint designs of analog beam selection and digital filters. The proposed joint designs achieve significantly higher sum-rates than the disjoint design benchmark. Supervised machine learning (ML) algorithms can efficiently approximate the input-output mapping functions of the beam selection decisions of the joint designs with low computational complexities. Since the training of ML algorithms is performed off-line, we propose a well-constructed joint design that combines multiple initializations, iterations, and selection features, as well as beam conflict control, i.e., the same beam cannot be used for multiple users. The numerical results indicate that ML algorithms can retain 99-100% of the original sum-rate results achieved by the proposed well-constructed designs.

Sampling and Update Frequencies in Proximal Variance Reduced Stochastic Gradient Methods

Variance reduced stochastic gradient methods have gained popularity in recent times. Several variants exist with different strategies for the storing and sampling of gradients. In this work we focus on the analysis of the interaction of these two aspects. We present and analyze a general proximal variance reduced gradient method under strong convexity assumptions. Special cases of the algorithm include SAGA, L-SVRG and their proximal variants. Our analysis sheds light on epoch-length selection and the need to balance the convergence of the iterates and how often gradients are stored. The analysis improves on other convergence rates found in literature and produces a new and faster converging sampling strategy for SAGA. Problem instances for which the predicted rates are the same as the practical rates are presented together with problems based on real world data.

Two Applications of Deep Learning in the Physical Layer of Communication Systems

Deep learning has proved itself to be a powerful tool to develop data-driven signal processing algorithms for challenging engineering problems. By learning the key features and characteristics of the input signals, instead of requiring a human to first identify and model them, learned algorithms can beat many man-made algorithms. In particular, deep neural networks are capable of learning the complicated features in nature-made signals, such as photos and audio recordings, and use them for classification and decision making. The situation is rather different in communication systems, where the information signals are man-made, the propagation channels are relatively easy to model, and we know how to operate close to the Shannon capacity limits. Does this mean that there is no role for deep learning in the development of future communication systems?

SVAG: Unified Convergence Results for SAG-SAGA Interpolation with Stochastic Variance Adjusted Gradient Descent

We analyze SVAG, a variance reduced stochastic gradient method with SAG and SAGA as special cases. Our convergence result for SVAG is the first to simultaneously capture both the biased low-variance method SAG and the unbiased high-variance method SAGA. In the case of SAGA, it matches previous upper bounds on the allowed step-size. The SVAG algorithm has a parameter that decides the bias-variance trade-off in the stochastic gradient estimate. We provide numerical examples demonstrating the intuition behind this bias-variance trade-off.

Efficient Proximal Mapping Computation for Unitarily Invariant Low-Rank Inducing Norms

Low-rank inducing unitarily invariant norms have been introduced to convexify problems with low-rank/sparsity constraint. They are the convex envelope of a unitary invariant norm and the indicator function of an upper bounding rank constraint. The most well-known member of this family is the so-called nuclear norm. To solve optimization problems involving such norms with proximal splitting methods, efficient ways of evaluating the proximal mapping of the low-rank inducing norms are needed. This is known for the nuclear norm, but not for most other members of the low-rank inducing family. This work supplies a framework that reduces the proximal mapping evaluation into a nested binary search, in which each iteration requires the solution of a much simpler problem. This simpler problem can often be solved analytically as it is demonstrated for the so-called low-rank inducing Frobenius and spectral norms. Moreover, the framework allows to compute the proximal mapping of compositions of these norms with increasing convex functions and the projections onto their epigraphs. This has the additional advantage that we can also deal with compositions of increasing convex functions and low-rank inducing norms in proximal splitting methods.

Low-Rank Inducing Norms with Optimality Interpretations

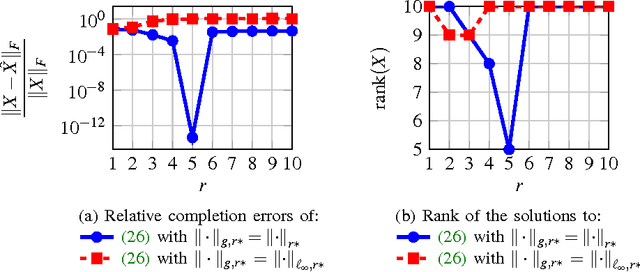
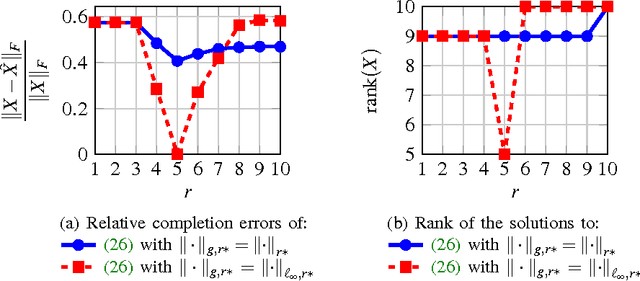
Optimization problems with rank constraints appear in many diverse fields such as control, machine learning and image analysis. Since the rank constraint is non-convex, these problems are often approximately solved via convex relaxations. Nuclear norm regularization is the prevailing convexifying technique for dealing with these types of problem. This paper introduces a family of low-rank inducing norms and regularizers which includes the nuclear norm as a special case. A posteriori guarantees on solving an underlying rank constrained optimization problem with these convex relaxations are provided. We evaluate the performance of the low-rank inducing norms on three matrix completion problems. In all examples, the nuclear norm heuristic is outperformed by convex relaxations based on other low-rank inducing norms. For two of the problems there exist low-rank inducing norms that succeed in recovering the partially unknown matrix, while the nuclear norm fails. These low-rank inducing norms are shown to be representable as semi-definite programs. Moreover, these norms have cheaply computable proximal mappings, which makes it possible to also solve problems of large size using first-order methods.

Low-rank Optimization with Convex Constraints

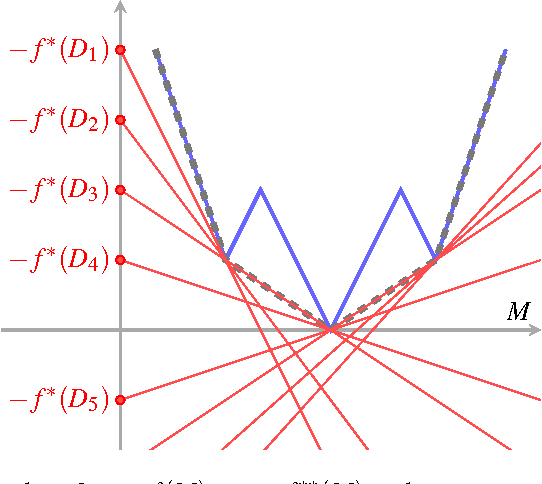
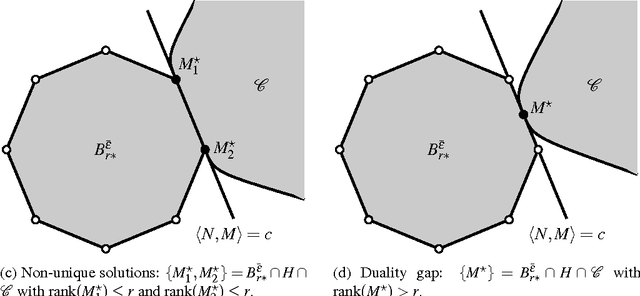
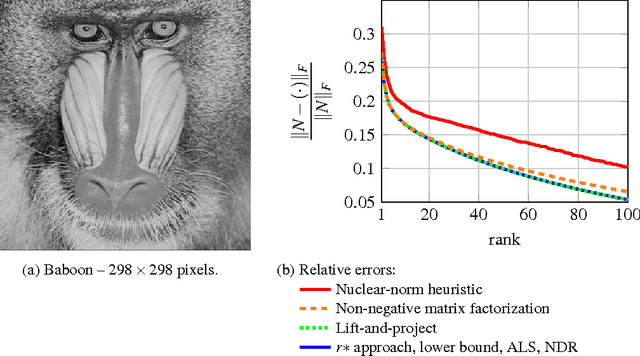
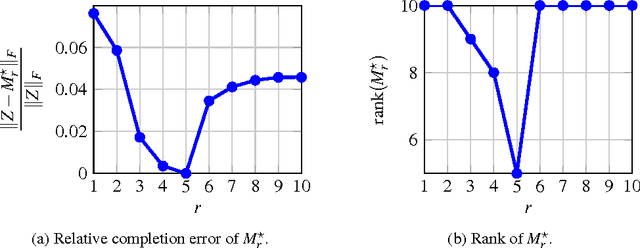
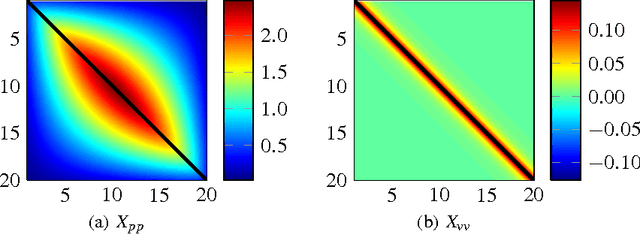
The problem of low-rank approximation with convex constraints, which appears in data analysis, system identification, model order reduction, low-order controller design and low-complexity modelling is considered. Given a matrix, the objective is to find a low-rank approximation that meets rank and convex constraints, while minimizing the distance to the matrix in the squared Frobenius norm. In many situations, this non-convex problem is convexified by nuclear norm regularization. However, we will see that the approximations obtained by this method may be far from optimal. In this paper, we propose an alternative convex relaxation that uses the convex envelope of the squared Frobenius norm and the rank constraint. With this approach, easily verifiable conditions are obtained under which the solutions to the convex relaxation and the original non-convex problem coincide. An SDP representation of the convex envelope is derived, which allows us to apply this approach to several known problems. Our example on optimal low-rank Hankel approximation/model reduction illustrates that the proposed convex relaxation performs consistently better than nuclear norm regularization and may outperform balanced truncation.

Local Convergence of Proximal Splitting Methods for Rank Constrained Problems

We analyze the local convergence of proximal splitting algorithms to solve optimization problems that are convex besides a rank constraint. For this, we show conditions under which the proximal operator of a function involving the rank constraint is locally identical to the proximal operator of its convex envelope, hence implying local convergence. The conditions imply that the non-convex algorithms locally converge to a solution whenever a convex relaxation involving the convex envelope can be expected to solve the non-convex problem.