FUnc-SNE: A flexible, Fast, and Unconstrained algorithm for neighbour embeddings

Neighbour embeddings (NE) allow the representation of high dimensional datasets into lower dimensional spaces and are often used in data visualisation. In practice, accelerated approximations are employed to handle very large datasets. Accelerating NE is challenging, and two main directions have been explored: very coarse approximations based on negative sampling (as in UMAP) achieve high effective speed but may lack quality in the extracted structures; less coarse approximations, as used in FIt-SNE or BH-t-SNE, offer better structure preservation at the cost of speed, while also restricting the target dimensionality to 2 or 3, limiting NE to visualisation. In some variants, the precision of these costlier accelerations also enables finer-grained control on the extracted structures through dedicated hyperparameters. This paper proposes to bridge the gab between both approaches by introducing a novel way to accelerate NE, requiring a small number of computations per iteration while maintaining good fine-grained structure preservation and flexibility through hyperparameter tuning, without limiting the dimensionality of the embedding space. The method was designed for interactive exploration of data; as such, it abandons the traditional two-phased approach of other NE methods, allowing instantaneous visual feedback when changing hyperparameters, even when these control processes happening on the high-dimensional side of the computations. Experiments using a publicly available, GPU accelerated GUI integration of the method show promising results in terms of speed, flexibility in the structures getting extracted, and show potential uses in broader machine learning contexts with minimal algorithmic modifications. Central to this algorithm is a novel approach to iterative approximate nearest neighbour search, which shows promising results compared to nearest neighbour descent.

SQuadMDS: a lean Stochastic Quartet MDS improving global structure preservation in neighbor embedding like t-SNE and UMAP

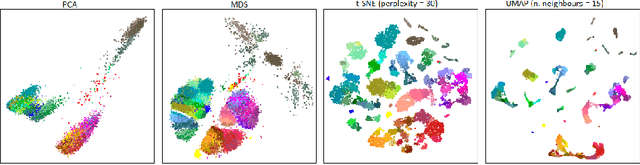
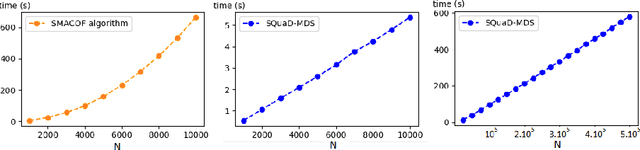
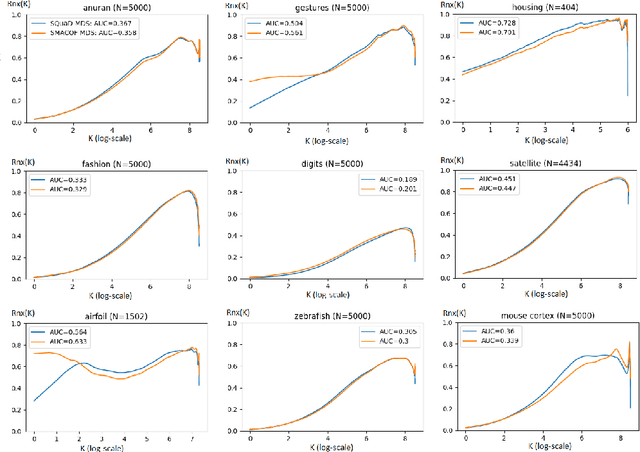
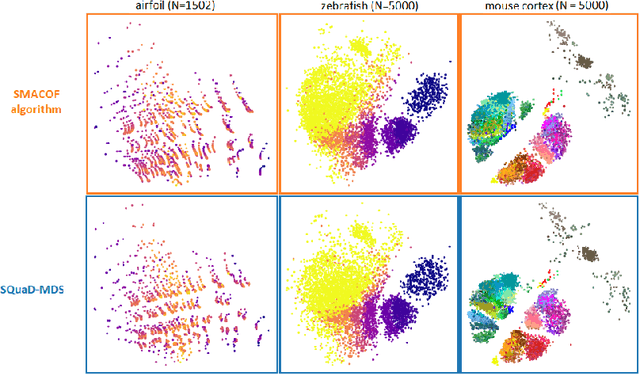
Multidimensional scaling is a statistical process that aims to embed high dimensional data into a lower-dimensional space; this process is often used for the purpose of data visualisation. Common multidimensional scaling algorithms tend to have high computational complexities, making them inapplicable on large data sets. This work introduces a stochastic, force directed approach to multidimensional scaling with a time and space complexity of O(N), with N data points. The method can be combined with force directed layouts of the family of neighbour embedding such as t-SNE, to produce embeddings that preserve both the global and the local structures of the data. Experiments assess the quality of the embeddings produced by the standalone version and its hybrid extension both quantitatively and qualitatively, showing competitive results outperforming state-of-the-art approaches. Codes are available at https://github.com/PierreLambert3/SQuaD-MDS-and-FItSNE-hybrid.