Countering adversarial evasion in regression analysis

Adversarial machine learning challenges the assumption that the underlying distribution remains consistent throughout the training and implementation of a prediction model. In particular, adversarial evasion considers scenarios where adversaries adapt their data to influence particular outcomes from established prediction models, such scenarios arise in applications such as spam email filtering, malware detection and fake-image generation, where security methods must be actively updated to keep up with the ever-improving generation of malicious data. Game theoretic models have been shown to be effective at modelling these scenarios and hence training resilient predictors against such adversaries. Recent advancements in the use of pessimistic bilevel optimsiation which remove assumptions about the convexity and uniqueness of the adversary's optimal strategy have proved to be particularly effective at mitigating threats to classifiers due to its ability to capture the antagonistic nature of the adversary. However, this formulation has not yet been adapted to regression scenarios. This article serves to propose a pessimistic bilevel optimisation program for regression scenarios which makes no assumptions on the convexity or uniqueness of the adversary's solutions.

Classification under strategic adversary manipulation using pessimistic bilevel optimisation

Adversarial machine learning concerns situations in which learners face attacks from active adversaries. Such scenarios arise in applications such as spam email filtering, malware detection and fake-image generation, where security methods must be actively updated to keep up with the ever improving generation of malicious data.We model these interactions between the learner and the adversary as a game and formulate the problem as a pessimistic bilevel optimisation problem with the learner taking the role of the leader. The adversary, modelled as a stochastic data generator, takes the role of the follower, generating data in response to the classifier. While existing models rely on the assumption that the adversary will choose the least costly solution leading to a convex lower-level problem with a unique solution, we present a novel model and solution method which do not make such assumptions. We compare these to the existing approach and see significant improvements in performance suggesting that relaxing these assumptions leads to a more realistic model.

A Relaxed Inertial Forward-Backward-Forward Algorithm for Solving Monotone Inclusions with Application to GANs

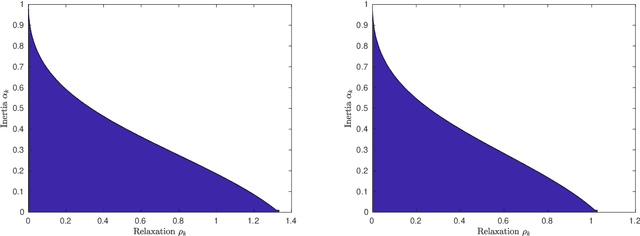
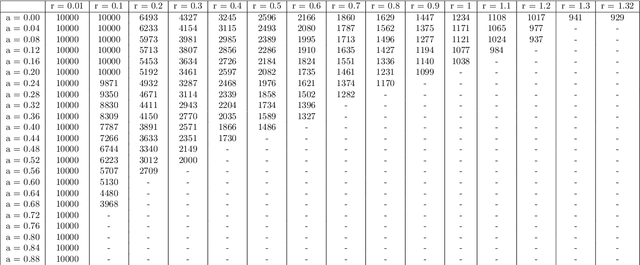
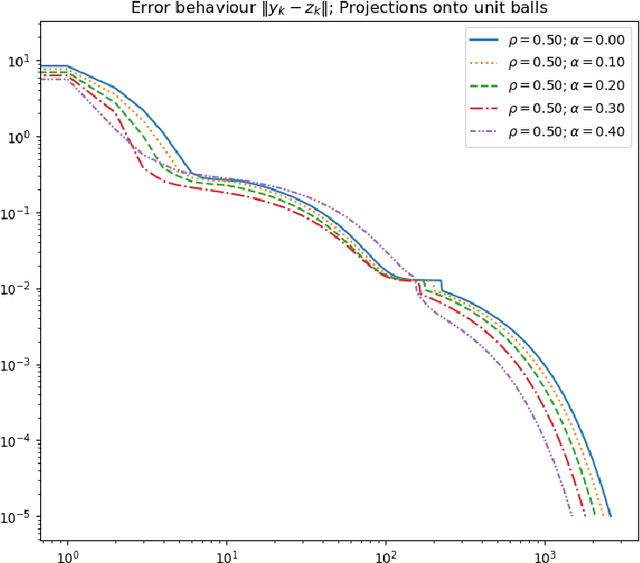
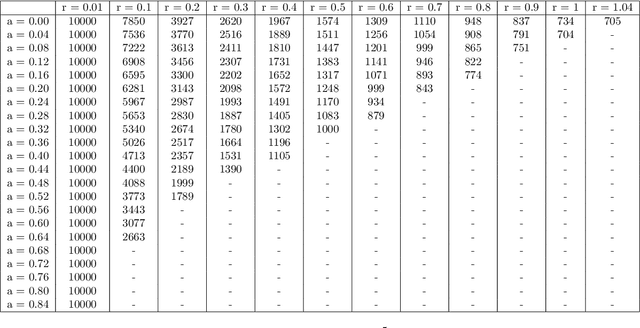
We introduce a relaxed inertial forward-backward-forward (RIFBF) splitting algorithm for approaching the set of zeros of the sum of a maximally monotone operator and a single-valued monotone and Lipschitz continuous operator. This work aims to extend Tseng's forward-backward-forward method by both using inertial effects as well as relaxation parameters. We formulate first a second order dynamical system which approaches the solution set of the monotone inclusion problem to be solved and provide an asymptotic analysis for its trajectories. We provide for RIFBF, which follows by explicit time discretization, a convergence analysis in the general monotone case as well as when applied to the solving of pseudo-monotone variational inequalities. We illustrate the proposed method by applications to a bilinear saddle point problem, in the context of which we also emphasize the interplay between the inertial and the relaxation parameters, and to the training of Generative Adversarial Networks (GANs).

Forward-backward-forward methods with variance reduction for stochastic variational inequalities

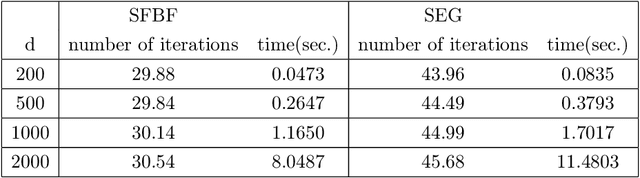
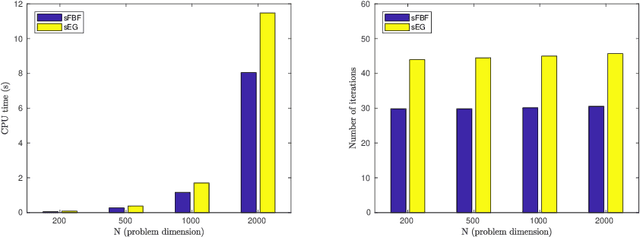
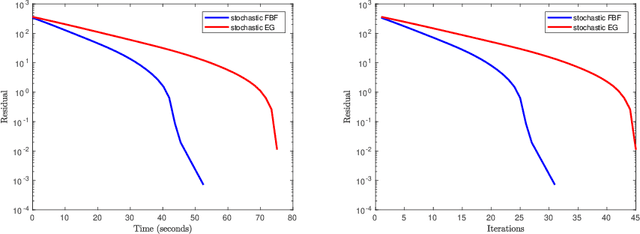
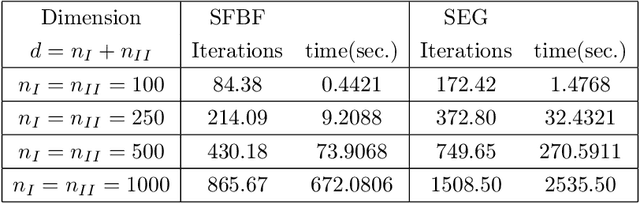
We develop a new stochastic algorithm with variance reduction for solving pseudo-monotone stochastic variational inequalities. Our method builds on Tseng's forward-backward-forward (FBF) algorithm, which is known in the deterministic literature to be a valuable alternative to Korpelevich's extragradient method when solving variational inequalities over a convex and closed set governed by pseudo-monotone, Lipschitz continuous operators. The main computational advantage of Tseng's algorithm is that it relies only on a single projection step and two independent queries of a stochastic oracle. Our algorithm incorporates a variance reduction mechanism and leads to almost sure (a.s.) convergence to an optimal solution. To the best of our knowledge, this is the first stochastic look-ahead algorithm achieving this by using only a single projection at each iteration..