DGNO: A Novel Physics-aware Neural Operator for Solving Forward and Inverse PDE Problems based on Deep, Generative Probabilistic Modeling

Solving parametric partial differential equations (PDEs) and associated PDE-based, inverse problems is a central task in engineering and physics, yet existing neural operator methods struggle with high-dimensional, discontinuous inputs and require large amounts of {\em labeled} training data. We propose the Deep Generative Neural Operator (DGNO), a physics-aware framework that addresses these challenges by leveraging a deep, generative, probabilistic model in combination with a set of lower-dimensional, latent variables that simultaneously encode PDE-inputs and PDE-outputs. This formulation can make use of unlabeled data and significantly improves inverse problem-solving, particularly for discontinuous or discrete-valued input functions. DGNO enforces physics constraints without labeled data by incorporating as virtual observables, weak-form residuals based on compactly supported radial basis functions (CSRBFs). These relax regularity constraints and eliminate higher-order derivatives from the objective function. We also introduce MultiONet, a novel neural operator architecture, which is a more expressive generalization of the popular DeepONet that significantly enhances the approximating power of the proposed model. These innovations make DGNO particularly effective for challenging forward and inverse, PDE-based problems, such as those involving multi-phase media. Numerical experiments demonstrate that DGNO achieves higher accuracy across multiple benchmarks while exhibiting robustness to noise and strong generalization to out-of-distribution cases. Its adaptability, and the ability to handle sparse, noisy data while providing probabilistic estimates, make DGNO a powerful tool for scientific and engineering applications.

Weak neural variational inference for solving Bayesian inverse problems without forward models: applications in elastography

In this paper, we introduce a novel, data-driven approach for solving high-dimensional Bayesian inverse problems based on partial differential equations (PDEs), called Weak Neural Variational Inference (WNVI). The method complements real measurements with virtual observations derived from the physical model. In particular, weighted residuals are employed as probes to the governing PDE in order to formulate and solve a Bayesian inverse problem without ever formulating nor solving a forward model. The formulation treats the state variables of the physical model as latent variables, inferred using Stochastic Variational Inference (SVI), along with the usual unknowns. The approximate posterior employed uses neural networks to approximate the inverse mapping from state variables to the unknowns. We illustrate the proposed method in a biomedical setting where we infer spatially varying material properties from noisy tissue deformation data. We demonstrate that WNVI is not only as accurate and more efficient than traditional methods that rely on repeatedly solving the (non)linear forward problem as a black-box, but it can also handle ill-posed forward problems (e.g., with insufficient boundary conditions).

Physics-Aware Neural Implicit Solvers for multiscale, parametric PDEs with applications in heterogeneous media

We propose Physics-Aware Neural Implicit Solvers (PANIS), a novel, data-driven framework for learning surrogates for parametrized Partial Differential Equations (PDEs). It consists of a probabilistic, learning objective in which weighted residuals are used to probe the PDE and provide a source of {\em virtual} data i.e. the actual PDE never needs to be solved. This is combined with a physics-aware implicit solver that consists of a much coarser, discretized version of the original PDE, which provides the requisite information bottleneck for high-dimensional problems and enables generalization in out-of-distribution settings (e.g. different boundary conditions). We demonstrate its capability in the context of random heterogeneous materials where the input parameters represent the material microstructure. We extend the framework to multiscale problems and show that a surrogate can be learned for the effective (homogenized) solution without ever solving the reference problem. We further demonstrate how the proposed framework can accommodate and generalize several existing learning objectives and architectures while yielding probabilistic surrogates that can quantify predictive uncertainty.

From concrete mixture to structural design -- a holistic optimization procedure in the presence of uncertainties

Designing civil structures such as bridges, dams or buildings is a complex task requiring many synergies from several experts. Each is responsible for different parts of the process. This is often done in a sequential manner, e.g. the structural engineer makes a design under the assumption of certain material properties (e.g. the strength class of the concrete), and then the material engineer optimizes the material with these restrictions. This paper proposes a holistic optimization procedure, which combines the concrete mixture design and structural simulations in a joint, forward workflow that we ultimately seek to invert. In this manner, new mixtures beyond standard ranges can be considered. Any design effort should account for the presence of uncertainties which can be aleatoric or epistemic as when data is used to calibrate physical models or identify models that fill missing links in the workflow. Inverting the causal relations established poses several challenges especially when these involve physics-based models which most often than not do not provide derivatives/sensitivities or when design constraints are present. To this end, we advocate Variational Optimization, with proposed extensions and appropriately chosen heuristics to overcome the aforementioned challenges. The proposed methodology is illustrated using the design of a precast concrete beam with the objective to minimize the global warming potential while satisfying a number of constraints associated with its load-bearing capacity after 28days according to the Eurocode, the demoulding time as computed by a complex nonlinear Finite Element model, and the maximum temperature during the hydration.

Multi-fidelity Constrained Optimization for Stochastic Black Box Simulators

Constrained optimization of the parameters of a simulator plays a crucial role in a design process. These problems become challenging when the simulator is stochastic, computationally expensive, and the parameter space is high-dimensional. One can efficiently perform optimization only by utilizing the gradient with respect to the parameters, but these gradients are unavailable in many legacy, black-box codes. We introduce the algorithm Scout-Nd (Stochastic Constrained Optimization for N dimensions) to tackle the issues mentioned earlier by efficiently estimating the gradient, reducing the noise of the gradient estimator, and applying multi-fidelity schemes to further reduce computational effort. We validate our approach on standard benchmarks, demonstrating its effectiveness in optimizing parameters highlighting better performance compared to existing methods.

A probabilistic, data-driven closure model for RANS simulations with aleatoric, model uncertainty

We propose a data-driven, closure model for Reynolds-averaged Navier-Stokes (RANS) simulations that incorporates aleatoric, model uncertainty. The proposed closure consists of two parts. A parametric one, which utilizes previously proposed, neural-network-based tensor basis functions dependent on the rate of strain and rotation tensor invariants. This is complemented by latent, random variables which account for aleatoric model errors. A fully Bayesian formulation is proposed, combined with a sparsity-inducing prior in order to identify regions in the problem domain where the parametric closure is insufficient and where stochastic corrections to the Reynolds stress tensor are needed. Training is performed using sparse, indirect data, such as mean velocities and pressures, in contrast to the majority of alternatives that require direct Reynolds stress data. For inference and learning, a Stochastic Variational Inference scheme is employed, which is based on Monte Carlo estimates of the pertinent objective in conjunction with the reparametrization trick. This necessitates derivatives of the output of the RANS solver, for which we developed an adjoint-based formulation. In this manner, the parametric sensitivities from the differentiable solver can be combined with the built-in, automatic differentiation capability of the neural network library in order to enable an end-to-end differentiable framework. We demonstrate the capability of the proposed model to produce accurate, probabilistic, predictive estimates for all flow quantities, even in regions where model errors are present, on a separated flow in the backward-facing step benchmark problem.

Interpretable reduced-order modeling with time-scale separation

Partial Differential Equations (PDEs) with high dimensionality are commonly encountered in computational physics and engineering. However, finding solutions for these PDEs can be computationally expensive, making model-order reduction crucial. We propose such a data-driven scheme that automates the identification of the time-scales involved and can produce stable predictions forward in time as well as under different initial conditions not included in the training data. To this end, we combine a non-linear autoencoder architecture with a time-continuous model for the latent dynamics in the complex space. It readily allows for the inclusion of sparse and irregularly sampled training data. The learned, latent dynamics are interpretable and reveal the different temporal scales involved. We show that this data-driven scheme can automatically learn the independent processes that decompose a system of linear ODEs along the eigenvectors of the system's matrix. Apart from this, we demonstrate the applicability of the proposed framework in a hidden Markov Model and the (discretized) Kuramoto-Shivashinsky (KS) equation. Additionally, we propose a probabilistic version, which captures predictive uncertainties and further improves upon the results of the deterministic framework.

Semi-supervised Invertible DeepONets for Bayesian Inverse Problems

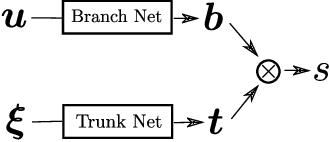
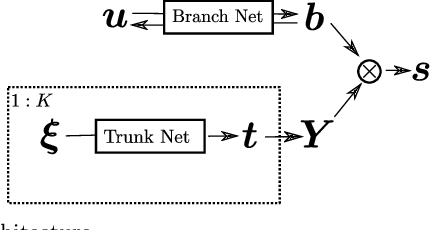
Deep Operator Networks (DeepONets) offer a powerful, data-driven tool for solving parametric PDEs by learning operators, i.e. maps between infinite-dimensional function spaces. In this work, we employ physics-informed DeepONets in the context of high-dimensional, Bayesian inverse problems. Traditional solution strategies necessitate an enormous, and frequently infeasible, number of forward model solves, as well as the computation of parametric derivatives. In order to enable efficient solutions, we extend DeepONets by employing a realNVP architecture which yields an invertible and differentiable map between the parametric input and the branch net output. This allows us to construct accurate approximations of the full posterior which can be readily adapted irrespective of the number of observations and the magnitude of the observation noise. As a result, no additional forward solves are required, nor is there any need for costly sampling procedures. We demonstrate the efficacy and accuracy of the proposed methodology in the context of inverse problems based on a anti-derivative, a reaction-diffusion and a Darcy-flow equation.

Physics-enhanced Neural Networks in the Small Data Regime

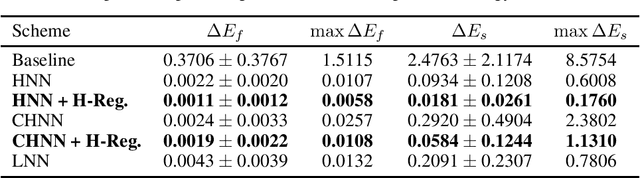
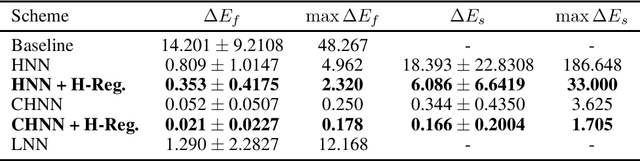
Identifying the dynamics of physical systems requires a machine learning model that can assimilate observational data, but also incorporate the laws of physics. Neural Networks based on physical principles such as the Hamiltonian or Lagrangian NNs have recently shown promising results in generating extrapolative predictions and accurately representing the system's dynamics. We show that by additionally considering the actual energy level as a regularization term during training and thus using physical information as inductive bias, the results can be further improved. Especially in the case where only small amounts of data are available, these improvements can significantly enhance the predictive capability. We apply the proposed regularization term to a Hamiltonian Neural Network (HNN) and Constrained Hamiltonian Neural Network (CHHN) for a single and double pendulum, generate predictions under unseen initial conditions and report significant gains in predictive accuracy.

Self-supervised optimization of random material microstructures in the small-data regime

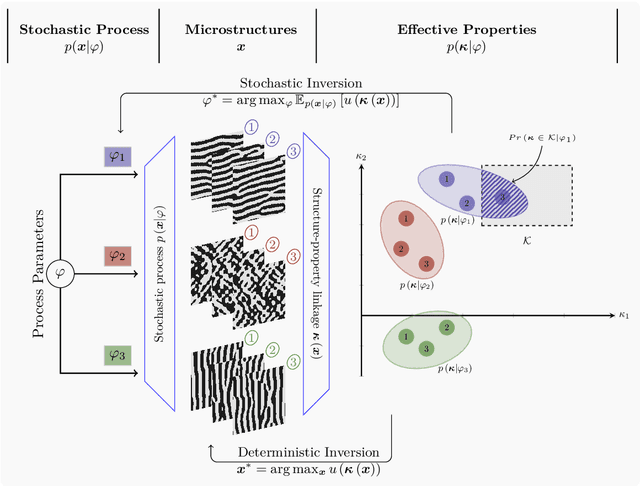
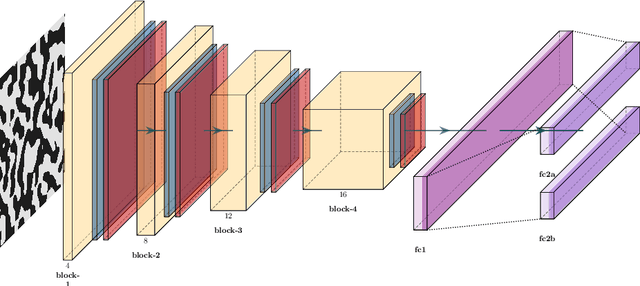
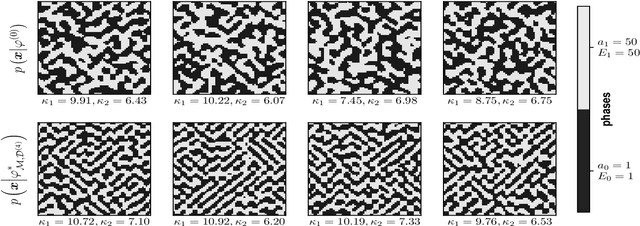
While the forward and backward modeling of the process-structure-property chain has received a lot of attention from the materials community, fewer efforts have taken into consideration uncertainties. Those arise from a multitude of sources and their quantification and integration in the inversion process are essential in meeting the materials design objectives. The first contribution of this paper is a flexible, fully probabilistic formulation of such optimization problems that accounts for the uncertainty in the process-structure and structure-property linkages and enables the identification of optimal, high-dimensional, process parameters. We employ a probabilistic, data-driven surrogate for the structure-property link which expedites computations and enables handling of non-differential objectives. We couple this with a novel active learning strategy, i.e. a self-supervised collection of data, which significantly improves accuracy while requiring small amounts of training data. We demonstrate its efficacy in optimizing the mechanical and thermal properties of two-phase, random media but envision its applicability encompasses a wide variety of microstructure-sensitive design problems.