An Optimal Policy for Learning Controllable Dynamics by Exploration

Controllable Markov chains describe the dynamics of sequential decision making tasks and are the central component in optimal control and reinforcement learning. In this work, we give the general form of an optimal policy for learning controllable dynamics in an unknown environment by exploring over a limited time horizon. This policy is simple to implement and efficient to compute, and allows an agent to ``learn by exploring" as it maximizes its information gain in a greedy fashion by selecting controls from a constraint set that changes over time during exploration. We give a simple parameterization for the set of controls, and present an algorithm for finding an optimal policy. The reason for this policy is due to the existence of certain types of states that restrict control of the dynamics; such as transient states, absorbing states, and non-backtracking states. We show why the occurrence of these states makes a non-stationary policy essential for achieving optimal exploration. Six interesting examples of controllable dynamics are treated in detail. Policy optimality is demonstrated using counting arguments, comparing with suboptimal policies, and by making use of a sequential improvement property from dynamic programming.

Learning controllable dynamics through informative exploration

Environments with controllable dynamics are usually understood in terms of explicit models. However, such models are not always available, but may sometimes be learned by exploring an environment. In this work, we investigate using an information measure called "predicted information gain" to determine the most informative regions of an environment to explore next. Applying methods from reinforcement learning allows good suboptimal exploring policies to be found, and leads to reliable estimates of the underlying controllable dynamics. This approach is demonstrated by comparing with several myopic exploration approaches.

Efficient Reinforcement Learning for Optimal Control with Natural Images

Reinforcement learning solves optimal control and sequential decision problems widely found in control systems engineering, robotics, and artificial intelligence. This work investigates optimal control over a sequence of natural images. The problem is formalized, and general conditions are derived for an image to be sufficient for implementing an optimal policy. Reinforcement learning is shown to be efficient only for certain types of image representations. This is demonstrated by developing a reinforcement learning benchmark that scales easily with number of states and length of horizon, and has optimal policies that are easily distinguished from suboptimal policies. Image representations given by overcomplete sparse codes are found to be computationally efficient for optimal control, using fewer computational resources to learn and evaluate optimal policies. For natural images of fixed size, representing each image as an overcomplete sparse code in a linear network is shown to increase network storage capacity by orders of magnitude beyond that possible for any complete code, allowing larger tasks with many more states to be solved. Sparse codes can be generated by devices with low energy requirements and low computational overhead.

A dynamic programming algorithm for informative measurements and near-optimal path-planning

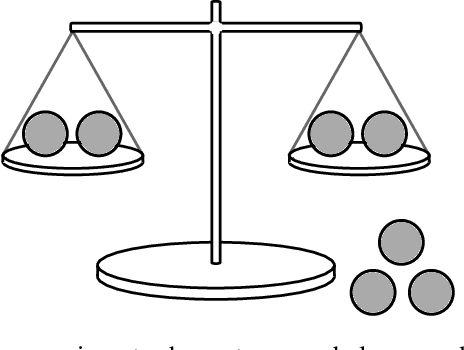
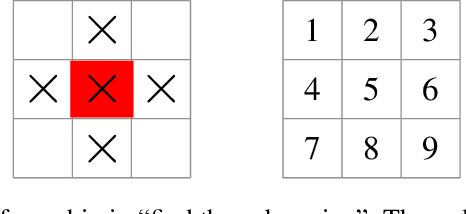
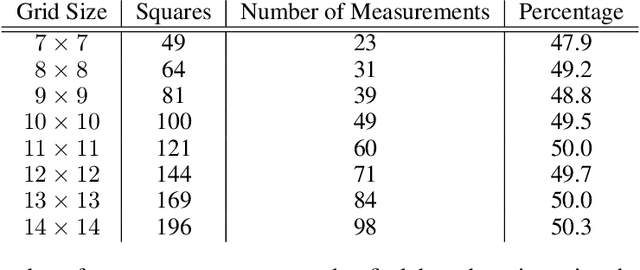
An informative measurement is the most efficient way to gain information about an unknown state. We give a first-principles derivation of a general-purpose dynamic programming algorithm that returns a sequence of informative measurements by sequentially maximizing the entropy of possible measurement outcomes. This algorithm can be used by an autonomous agent or robot to decide where best to measure next, planning a path corresponding to an optimal sequence of informative measurements. This algorithm is applicable to states and controls that are continuous or discrete, and agent dynamics that is either stochastic or deterministic; including Markov decision processes. Recent results from approximate dynamic programming and reinforcement learning, including on-line approximations such as rollout and Monte Carlo tree search, allow an agent or robot to solve the measurement task in real-time. The resulting near-optimal solutions include non-myopic paths and measurement sequences that can generally outperform, sometimes substantially, commonly-used greedy heuristics such as maximizing the entropy of each measurement outcome. This is demonstrated for a global search problem, where on-line planning with an extended local search is found to reduce the number of measurements in the search by half.