Physics-informed ConvNet: Learning Physical Field from a Shallow Neural Network

Big-data-based artificial intelligence (AI) supports profound evolution in almost all of science and technology. However, modeling and forecasting multi-physical systems remain a challenge due to unavoidable data scarcity and noise. Improving the generalization ability of neural networks by "teaching" domain knowledge and developing a new generation of models combined with the physical laws have become promising areas of machine learning research. Different from "deep" fully-connected neural networks embedded with physical information (PINN), a novel shallow framework named physics-informed convolutional network (PICN) is recommended from a CNN perspective, in which the physical field is generated by a deconvolution layer and a single convolution layer. The difference fields forming the physical operator are constructed using the pre-trained shallow convolution layer. An efficient linear interpolation network calculates the loss function involving boundary conditions and the physical constraints in irregular geometry domains. The effectiveness of the current development is illustrated through some numerical cases involving the solving (and estimation) of nonlinear physical operator equations and recovering physical information from noisy observations. Its potential advantage in approximating physical fields with multi-frequency components indicates that PICN may become an alternative neural network solver in physics-informed machine learning.

Parallel frequency function-deep neural network for efficient complex broadband signal approximation

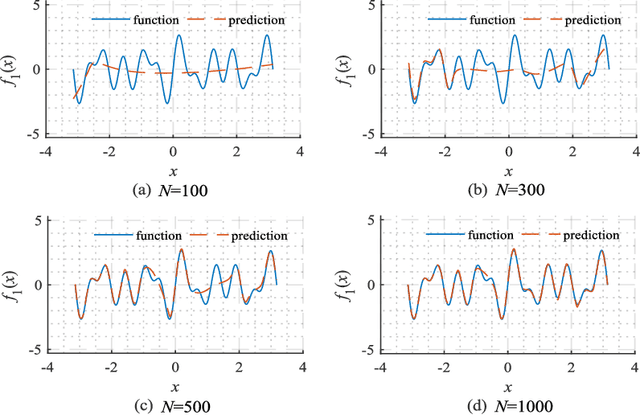
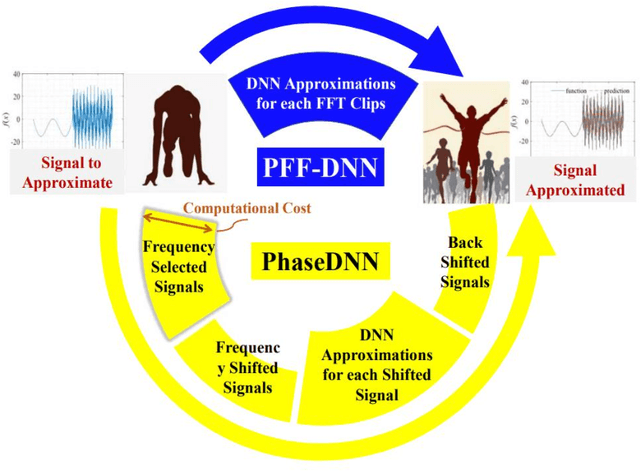
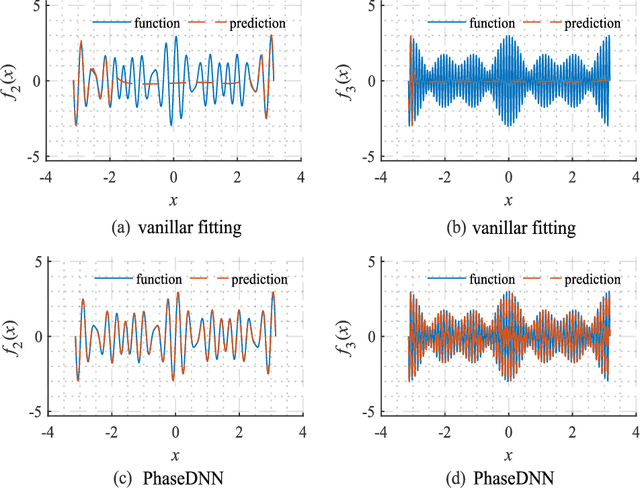
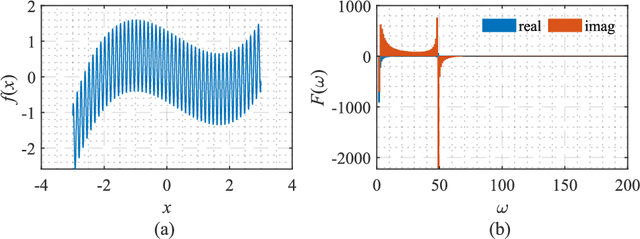
A neural network is essentially a high-dimensional complex mapping model by adjusting network weights for feature fitting. However, the spectral bias in network training leads to unbearable training epochs for fitting the high-frequency components in broadband signals. To improve the fitting efficiency of high-frequency components, the PhaseDNN was proposed recently by combining complex frequency band extraction and frequency shift techniques [Cai et al. SIAM J. SCI. COMPUT. 42, A3285 (2020)]. Our paper is devoted to an alternative candidate for fitting complex signals with high-frequency components. Here, a parallel frequency function-deep neural network (PFF-DNN) is proposed to suppress computational overhead while ensuring fitting accuracy by utilizing fast Fourier analysis of broadband signals and the spectral bias nature of neural networks. The effectiveness and efficiency of the proposed PFF-DNN method are verified based on detailed numerical experiments for six typical broadband signals.