Regularization for convolutional kernel tensors to avoid unstable gradient problem in convolutional neural networks

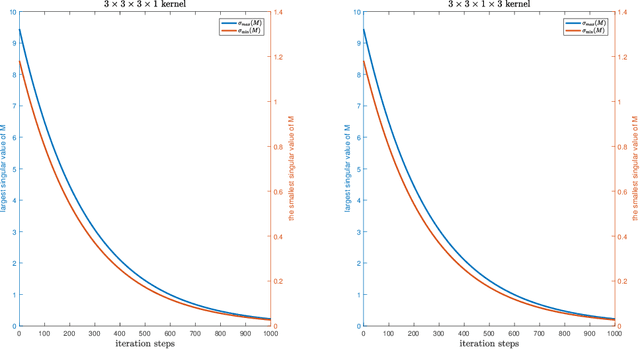
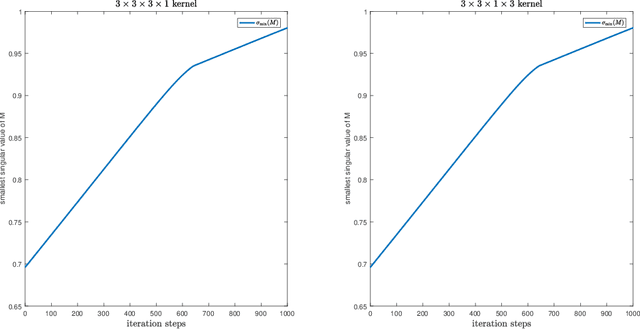
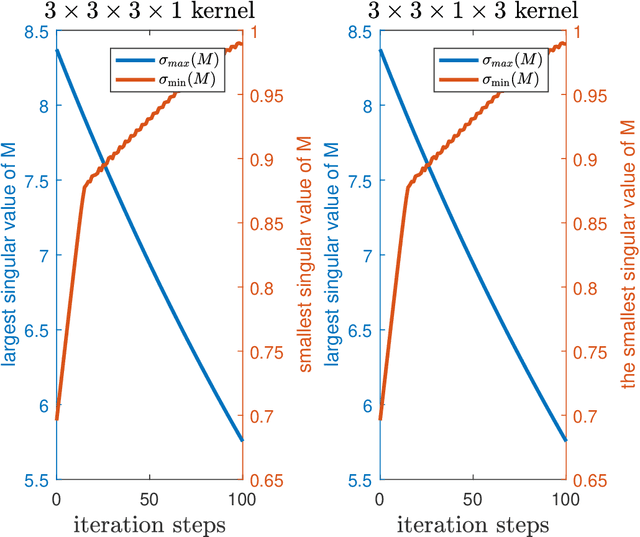
Convolutional neural networks are very popular nowadays. Training neural networks is not an easy task. Each convolution corresponds to a structured transformation matrix. In order to help avoid the exploding/vanishing gradient problem, it is desirable that the singular values of each transformation matrix are not large/small in the training process. We propose three new regularization terms for a convolutional kernel tensor to constrain the singular values of each transformation matrix. We show how to carry out the gradient type methods, which provides new insight about the training of convolutional neural networks.

A Frobenius norm regularization method for convolutional kernels to avoid unstable gradient problem

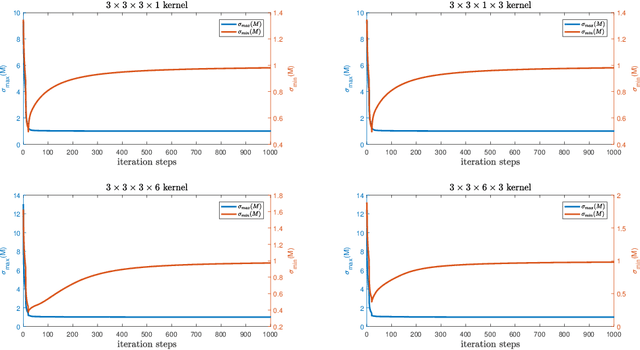
Convolutional neural network is a very important model of deep learning. It can help avoid the exploding/vanishing gradient problem and improve the generalizability of a neural network if the singular values of the Jacobian of a layer are bounded around $1$ in the training process. We propose a new penalty function for a convolutional kernel to let the singular values of the corresponding transformation matrix are bounded around $1$. We show how to carry out the gradient type methods. The penalty is about the structured transformation matrix corresponding to a convolutional kernel. This provides a new regularization method about the weights of convolutional layers.