CGAN-EB: A Non-parametric Empirical Bayes Method for Crash Hotspot Identification Using Conditional Generative Adversarial Networks: A Real-world Crash Data Study

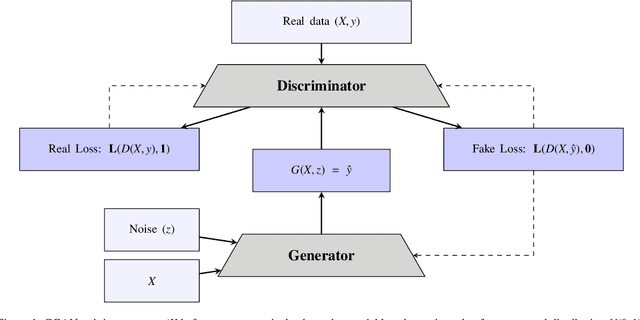
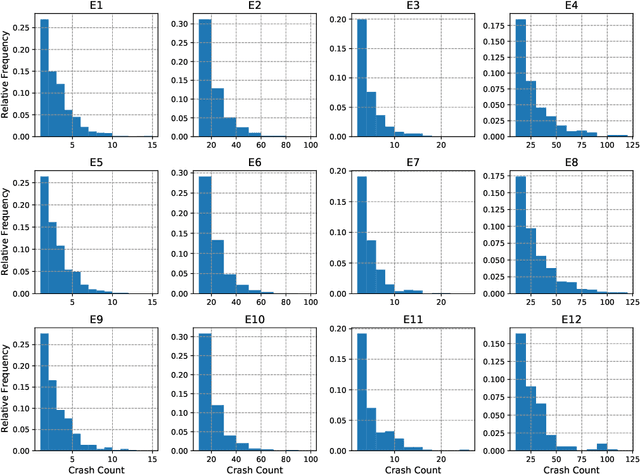
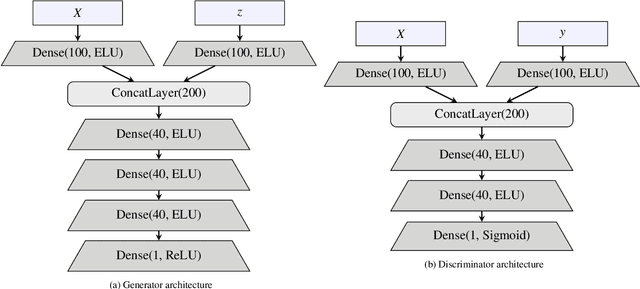
The empirical Bayes (EB) method based on parametric statistical models such as the negative binomial (NB) has been widely used for ranking sites in road network safety screening process. This paper is the continuation of the authors previous research, where a novel non-parametric EB method for modelling crash frequency data data based on Conditional Generative Adversarial Networks (CGAN) was proposed and evaluated over several simulated crash data sets. Unlike parametric approaches, there is no need for a pre-specified underlying relationship between dependent and independent variables in the proposed CGAN-EB and they are able to model any types of distributions. The proposed methodology is now applied to a real-world data set collected for road segments from 2012 to 2017 in Washington State. The performance of CGAN-EB in terms of model fit, predictive performance and network screening outcomes is compared with the conventional approach (NB-EB) as a benchmark. The results indicate that the proposed CGAN-EB approach outperforms NB-EB in terms of prediction power and hotspot identification tests.

CGAN-EB: A Non-parametric Empirical Bayes Method for Crash Hotspot Identification Using Conditional Generative Adversarial Networks: A Simulated Crash Data Study

In this paper, a new non-parametric empirical Bayes approach called CGAN-EB is proposed for approximating empirical Bayes (EB) estimates in traffic locations (e.g., road segments) which benefits from the modeling advantages of deep neural networks, and its performance is compared in a simulation study with the traditional approach based on negative binomial model (NB-EB). The NB-EB uses negative binomial model in order to model the crash data and is the most common approach in practice. To model the crash data in the proposed CGAN-EB, conditional generative adversarial network is used, which is a powerful deep neural network based method that can model any types of distributions. A number of simulation experiments are designed and conducted to evaluate the CGAN-EB performance in different conditions and compare it with the NB-EB. The results show that CGAN-EB performs as well as NB-EB when conditions favor the NB-EB model (i.e. data conform to the assumptions of the NB model) and outperforms NB-EB in experiments reflecting conditions frequently encountered in practice, specifically low sample means, and when crash frequency does not follow a log-linear relationship with covariates.