Regression for sets of polynomial equations

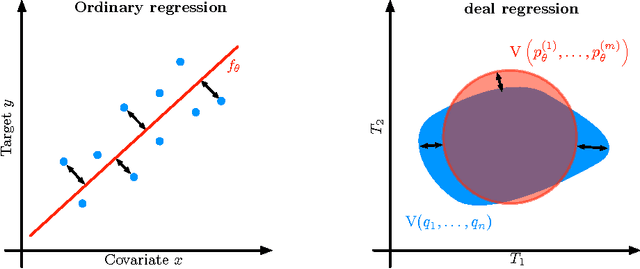
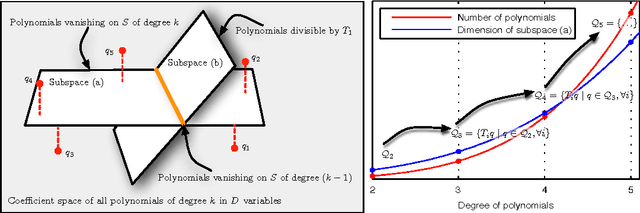
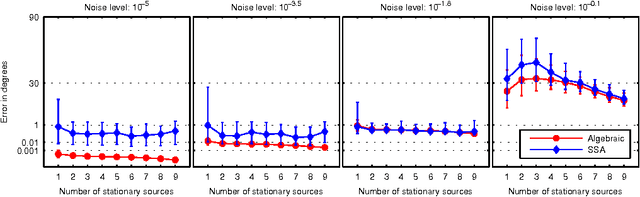
We propose a method called ideal regression for approximating an arbitrary system of polynomial equations by a system of a particular type. Using techniques from approximate computational algebraic geometry, we show how we can solve ideal regression directly without resorting to numerical optimization. Ideal regression is useful whenever the solution to a learning problem can be described by a system of polynomial equations. As an example, we demonstrate how to formulate Stationary Subspace Analysis (SSA), a source separation problem, in terms of ideal regression, which also yields a consistent estimator for SSA. We then compare this estimator in simulations with previous optimization-based approaches for SSA.

Feature Extraction for Change-Point Detection using Stationary Subspace Analysis

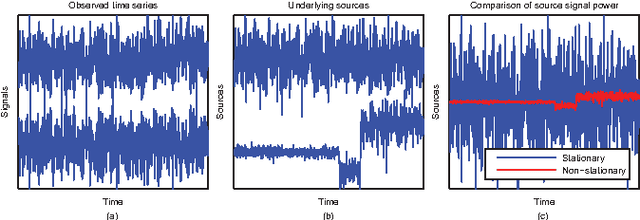
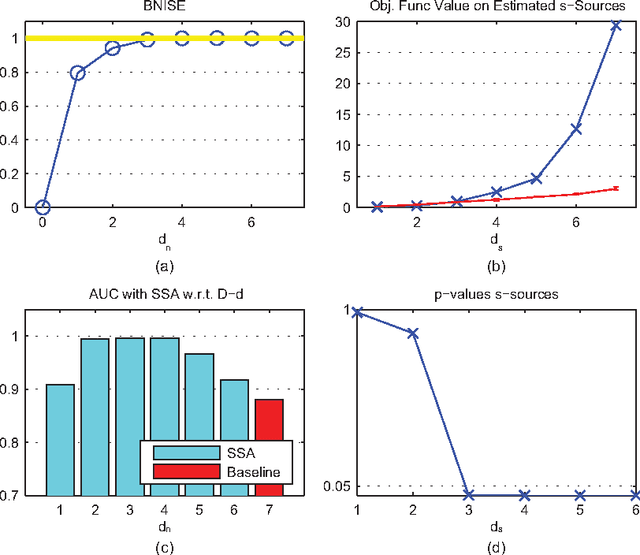
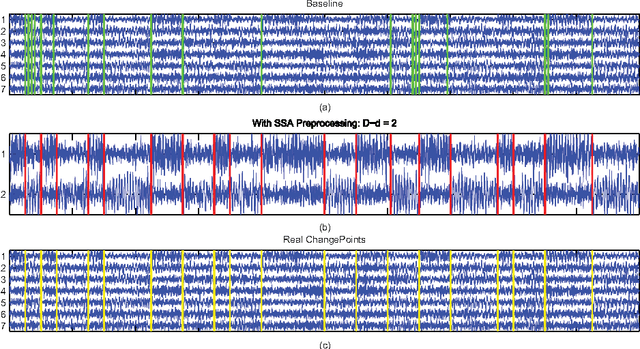
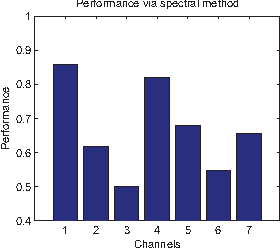
Detecting changes in high-dimensional time series is difficult because it involves the comparison of probability densities that need to be estimated from finite samples. In this paper, we present the first feature extraction method tailored to change point detection, which is based on an extended version of Stationary Subspace Analysis. We reduce the dimensionality of the data to the most non-stationary directions, which are most informative for detecting state changes in the time series. In extensive simulations on synthetic data we show that the accuracy of three change point detection algorithms is significantly increased by a prior feature extraction step. These findings are confirmed in an application to industrial fault monitoring.