Learning Powers of Poisson Binomial Distributions

We introduce the problem of simultaneously learning all powers of a Poisson Binomial Distribution (PBD). A PBD of order $n$ is the distribution of a sum of $n$ mutually independent Bernoulli random variables $X_i$, where $\mathbb{E}[X_i] = p_i$. The $k$'th power of this distribution, for $k$ in a range $[m]$, is the distribution of $P_k = \sum_{i=1}^n X_i^{(k)}$, where each Bernoulli random variable $X_i^{(k)}$ has $\mathbb{E}[X_i^{(k)}] = (p_i)^k$. The learning algorithm can query any power $P_k$ several times and succeeds in learning all powers in the range, if with probability at least $1- \delta$: given any $k \in [m]$, it returns a probability distribution $Q_k$ with total variation distance from $P_k$ at most $\epsilon$. We provide almost matching lower and upper bounds on query complexity for this problem. We first show a lower bound on the query complexity on PBD powers instances with many distinct parameters $p_i$ which are separated, and we almost match this lower bound by examining the query complexity of simultaneously learning all the powers of a special class of PBD's resembling the PBD's of our lower bound. We study the fundamental setting of a Binomial distribution, and provide an optimal algorithm which uses $O(1/\epsilon^2)$ samples. Diakonikolas, Kane and Stewart [COLT'16] showed a lower bound of $\Omega(2^{1/\epsilon})$ samples to learn the $p_i$'s within error $\epsilon$. The question whether sampling from powers of PBDs can reduce this sampling complexity, has a negative answer since we show that the exponential number of samples is inevitable. Having sampling access to the powers of a PBD we then give a nearly optimal algorithm that learns its $p_i$'s. To prove our two last lower bounds we extend the classical minimax risk definition from statistics to estimating functions of sequences of distributions.

On the performance of approximate equilibria in congestion games

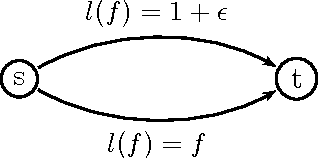
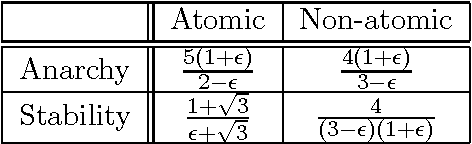
We study the performance of approximate Nash equilibria for linear congestion games. We consider how much the price of anarchy worsens and how much the price of stability improves as a function of the approximation factor $\epsilon$. We give (almost) tight upper and lower bounds for both the price of anarchy and the price of stability for atomic and non-atomic congestion games. Our results not only encompass and generalize the existing results of exact equilibria to $\epsilon$-Nash equilibria, but they also provide a unified approach which reveals the common threads of the atomic and non-atomic price of anarchy results. By expanding the spectrum, we also cast the existing results in a new light. For example, the Pigou network, which gives tight results for exact Nash equilibria of selfish routing, remains tight for the price of stability of $\epsilon$-Nash equilibria but not for the price of anarchy.