Fisher information lower bounds for sampling

We prove two lower bounds for the complexity of non-log-concave sampling within the framework of Balasubramanian et al. (2022), who introduced the use of Fisher information (FI) bounds as a notion of approximate first-order stationarity in sampling. Our first lower bound shows that averaged LMC is optimal for the regime of large FI by reducing the problem of finding stationary points in non-convex optimization to sampling. Our second lower bound shows that in the regime of small FI, obtaining a FI of at most $\varepsilon^2$ from the target distribution requires $\text{poly}(1/\varepsilon)$ queries, which is surprising as it rules out the existence of high-accuracy algorithms (e.g., algorithms using Metropolis-Hastings filters) in this context.

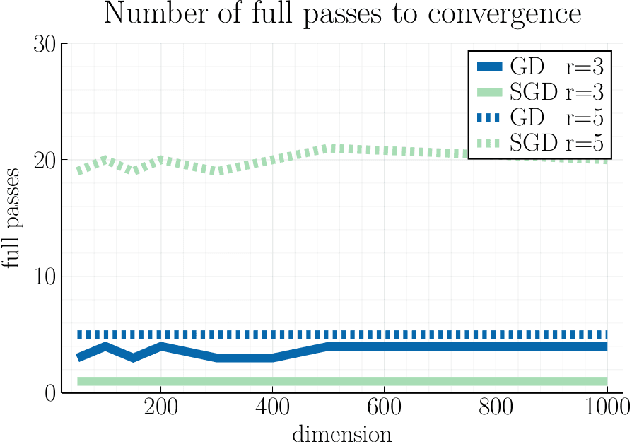
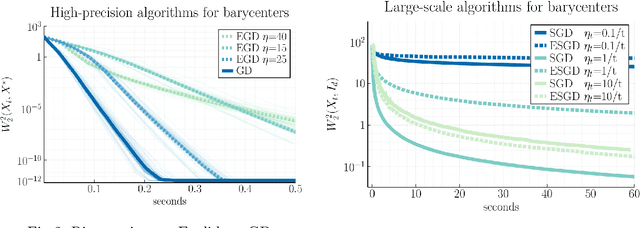
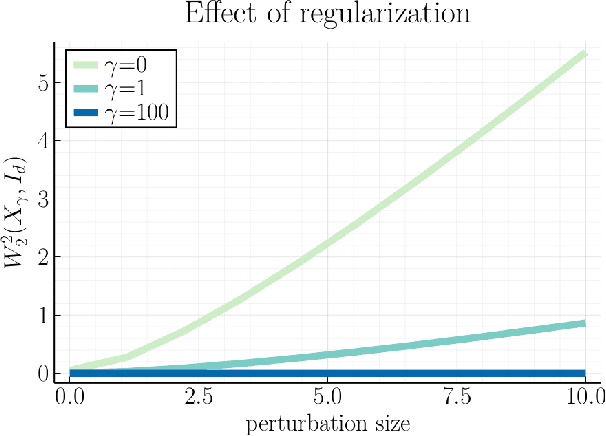
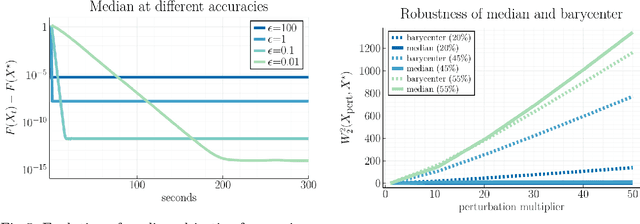
Averaging on the Bures-Wasserstein manifold: dimension-free convergence of gradient descent

We study first-order optimization algorithms for computing the barycenter of Gaussian distributions with respect to the optimal transport metric. Although the objective is geodesically non-convex, Riemannian GD empirically converges rapidly, in fact faster than off-the-shelf methods such as Euclidean GD and SDP solvers. This stands in stark contrast to the best-known theoretical results for Riemannian GD, which depend exponentially on the dimension. In this work, we prove new geodesic convexity results which provide stronger control of the iterates, yielding a dimension-free convergence rate. Our techniques also enable the analysis of two related notions of averaging, the entropically-regularized barycenter and the geometric median, providing the first convergence guarantees for Riemannian GD for these problems.

The query complexity of sampling from strongly log-concave distributions in one dimension

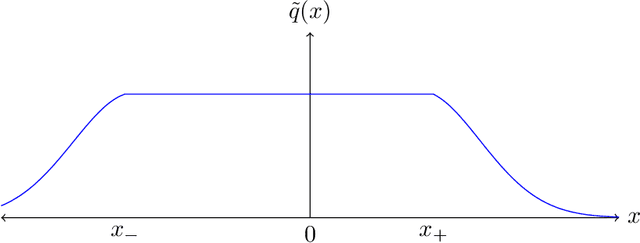
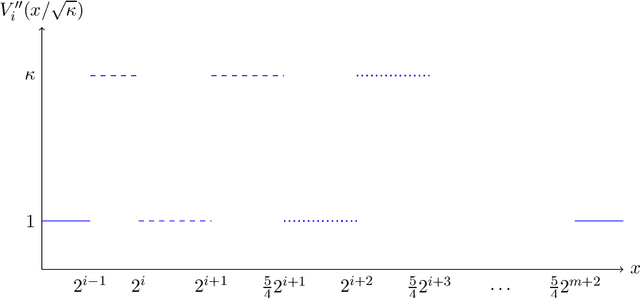
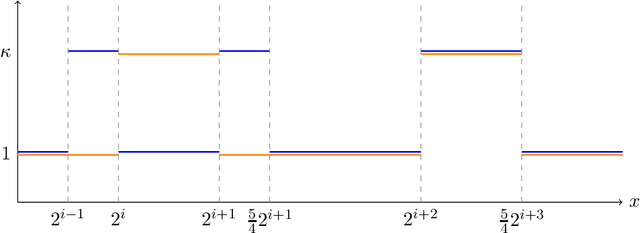
We establish the first tight lower bound of $\Omega(\log\log\kappa)$ on the query complexity of sampling from the class of strongly log-concave and log-smooth distributions with condition number $\kappa$ in one dimension. Whereas existing guarantees for MCMC-based algorithms scale polynomially in $\kappa$, we introduce a novel algorithm based on rejection sampling that closes this doubly exponential gap.

Rejection sampling from shape-constrained distributions in sublinear time

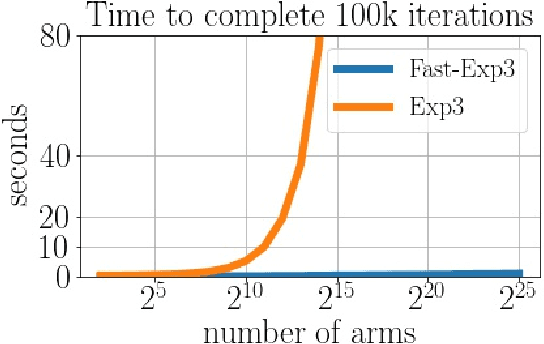
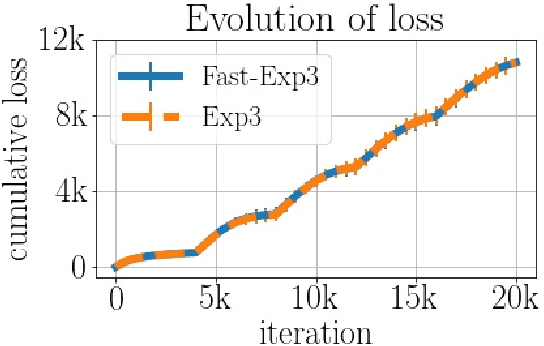
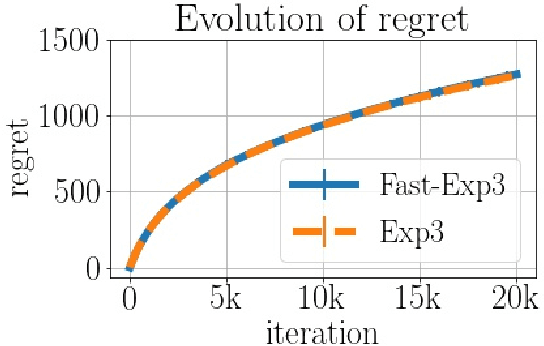
We consider the task of generating exact samples from a target distribution, known up to normalization, over a finite alphabet. The classical algorithm for this task is rejection sampling, and although it has been used in practice for decades, there is surprisingly little study of its fundamental limitations. In this work, we study the query complexity of rejection sampling in a minimax framework for various classes of discrete distributions. Our results provide new algorithms for sampling whose complexity scales sublinearly with the alphabet size. When applied to adversarial bandits, we show that a slight modification of the Exp3 algorithm reduces the per-iteration complexity from $\mathcal O(K)$ to $\mathcal O(\log^2 K)$, where $K$ is the number of arms.