The multilayer random dot product graph

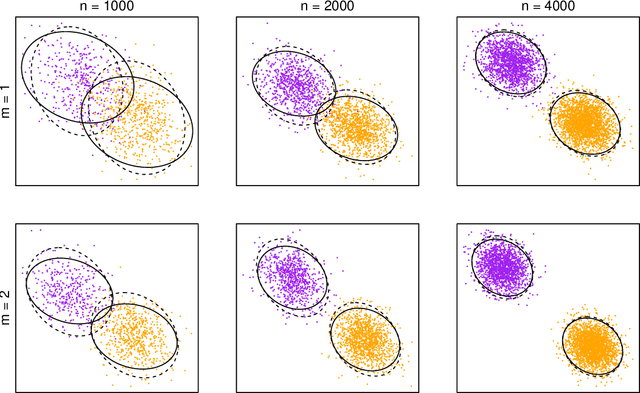
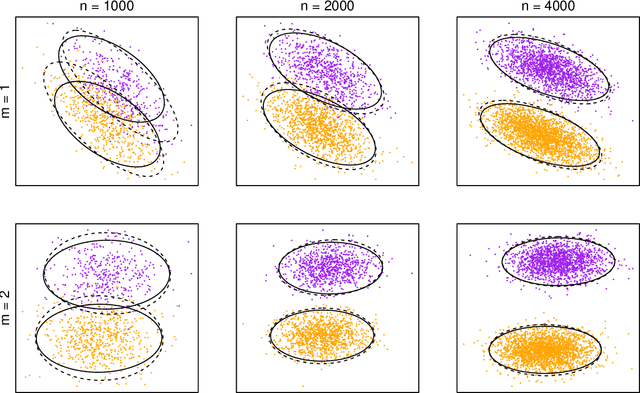
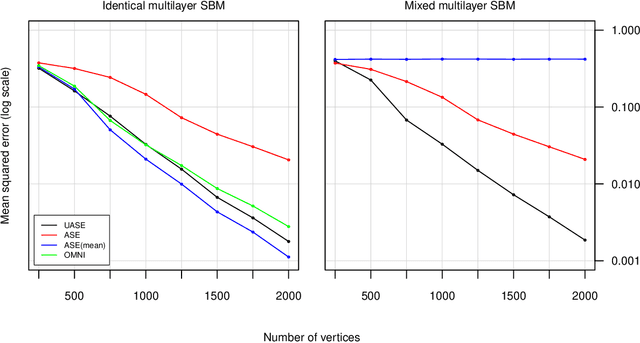
We present an extension of the latent position network model known as the generalised random dot product graph to accommodate multiple graphs with a common node structure, based on a matrix representation of the natural third-order tensor created from the adjacency matrices of these graphs. Theoretical results concerning the asymptotic behaviour of the node representations obtained by spectral embedding are established, showing that after the application of a linear transformation these converge uniformly in the Euclidean norm to the latent positions with a Gaussian error. The flexibility of the model is demonstrated through application to the tasks of latent position recovery and two-graph hypothesis testing, in which it performs favourably compared to existing models. Empirical improvements in link prediction over single graph embeddings are exhibited in a cyber-security example.

Manifold structure in graph embeddings

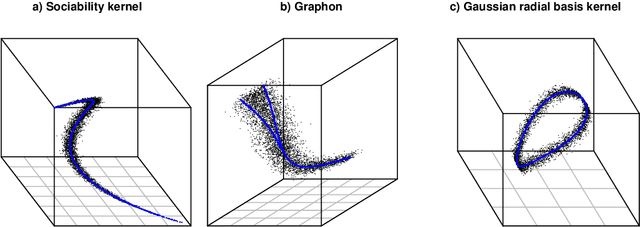
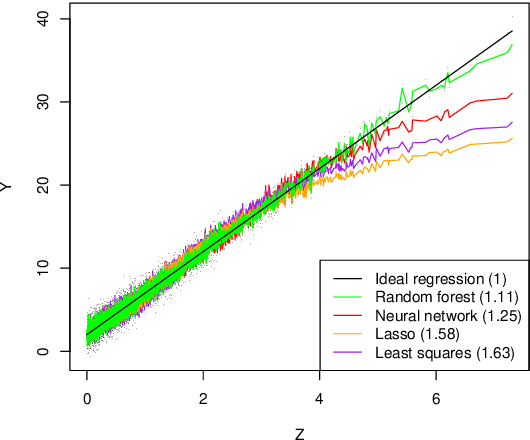
Statistical analysis of a graph often starts with embedding, the process of representing its nodes as points in space. How to choose the embedding dimension is a nuanced decision in practice, but in theory a notion of true dimension is often available. In spectral embedding, this dimension may be very high. However, this paper shows that existing random graph models, including graphon and other latent position models, predict the data should live near a much lower dimensional set. One may therefore circumvent the curse of dimensionality by employing methods which exploit hidden manifold structure.

Spectral clustering in the weighted stochastic block model

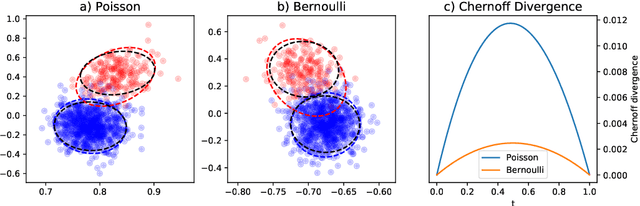
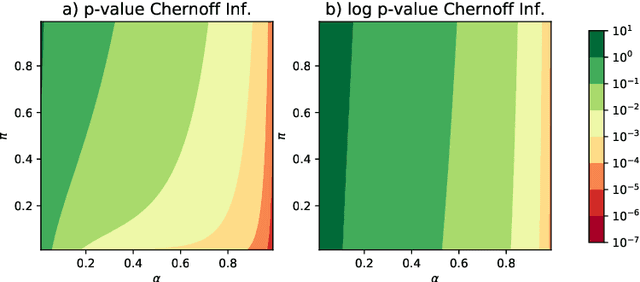
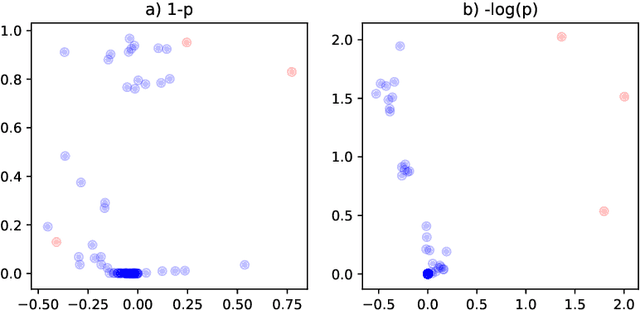
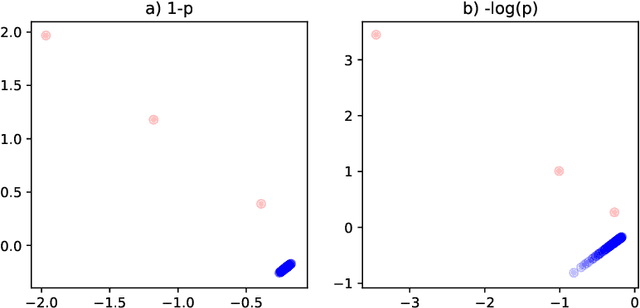
This paper is concerned with the statistical analysis of a real-valued symmetric data matrix. We assume a weighted stochastic block model: the matrix indices, taken to represent nodes, can be partitioned into communities so that all entries corresponding to a given community pair are replicates of the same random variable. Extending results previously known only for unweighted graphs, we provide a limit theorem showing that the point cloud obtained from spectrally embedding the data matrix follows a Gaussian mixture model where each community is represented with an elliptical component. We can therefore formally evaluate how well the communities separate under different data transformations, for example, whether it is productive to "take logs". We find that performance is invariant to affine transformation of the entries, but this expected and desirable feature hinges on adaptively selecting the eigenvectors according to eigenvalue magnitude and using Gaussian clustering. We present a network anomaly detection problem with cyber-security data where the matrix of log p-values, as opposed to p-values, has both theoretical and empirical advantages.

A statistical interpretation of spectral embedding: the generalised random dot product graph

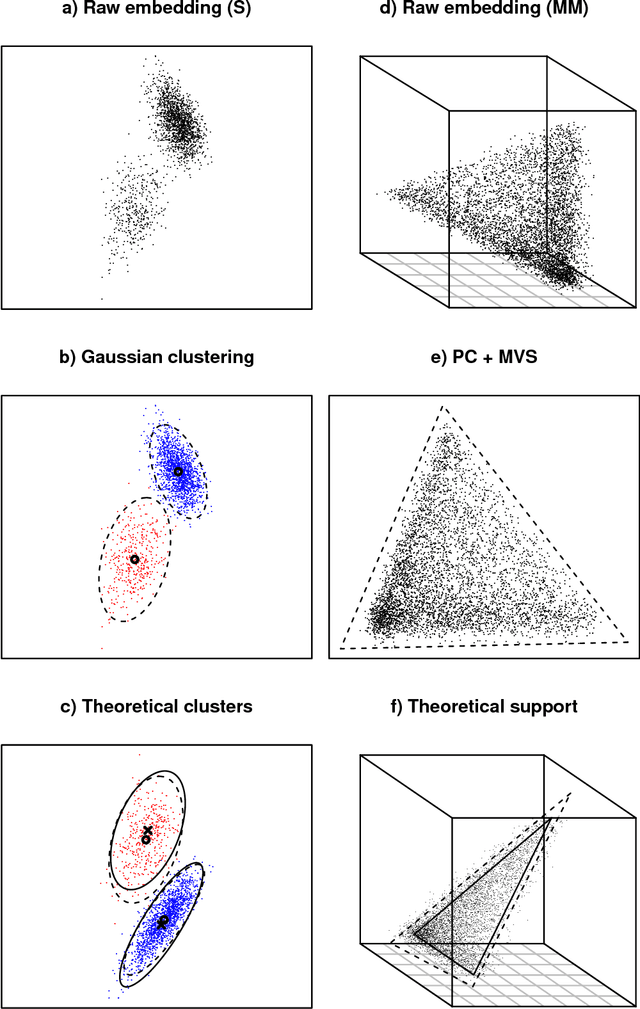
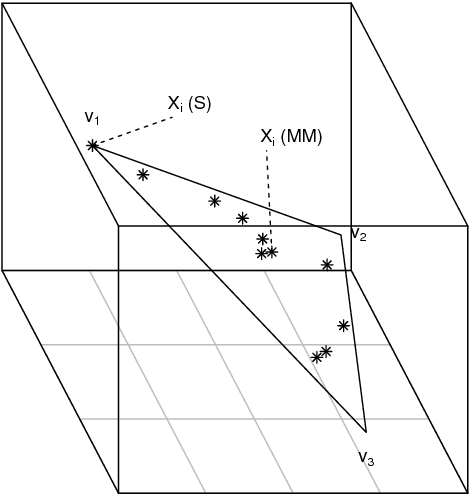
A generalisation of a latent position network model known as the random dot product graph model is considered. The resulting model may be of independent interest because it has the unique property of representing a mixture of connectivity behaviours as the corresponding convex combination in latent space. We show that, whether the normalised Laplacian or adjacency matrix is used, the vector representations of nodes obtained by spectral embedding provide strongly consistent latent position estimates with asymptotically Gaussian error. Direct methodological consequences follow from the observation that the well-known mixed membership and standard stochastic block models are special cases where the latent positions live respectively inside or on the vertices of a simplex. Estimation via spectral embedding can therefore be achieved by respectively estimating this simplicial support, or fitting a Gaussian mixture model. In the latter case, the use of $K$-means, as has been previously recommended, is suboptimal and for identifiability reasons unsound. Empirical improvements in link prediction, as well as the potential to uncover much richer latent structure (than available under the mixed membership or standard stochastic block models) are demonstrated in a cyber-security example.