Computing Optimal Transport Maps and Wasserstein Barycenters Using Conditional Normalizing Flows

We present a novel method for efficiently computing optimal transport maps and Wasserstein barycenters in high-dimensional spaces. Our approach uses conditional normalizing flows to approximate the input distributions as invertible pushforward transformations from a common latent space. This makes it possible to directly solve the primal problem using gradient-based minimization of the transport cost, unlike previous methods that rely on dual formulations and complex adversarial optimization. We show how this approach can be extended to compute Wasserstein barycenters by solving a conditional variance minimization problem. A key advantage of our conditional architecture is that it enables the computation of barycenters for hundreds of input distributions, which was computationally infeasible with previous methods. Our numerical experiments illustrate that our approach yields accurate results across various high-dimensional tasks and compares favorably with previous state-of-the-art methods.

Deep Learning for Continuous-time Stochastic Control with Jumps

In this paper, we introduce a model-based deep-learning approach to solve finite-horizon continuous-time stochastic control problems with jumps. We iteratively train two neural networks: one to represent the optimal policy and the other to approximate the value function. Leveraging a continuous-time version of the dynamic programming principle, we derive two different training objectives based on the Hamilton-Jacobi-Bellman equation, ensuring that the networks capture the underlying stochastic dynamics. Empirical evaluations on different problems illustrate the accuracy and scalability of our approach, demonstrating its effectiveness in solving complex, high-dimensional stochastic control tasks.

Gradient descent provably escapes saddle points in the training of shallow ReLU networks

Dynamical systems theory has recently been applied in optimization to prove that gradient descent algorithms avoid so-called strict saddle points of the loss function. However, in many modern machine learning applications, the required regularity conditions are not satisfied. In particular, this is the case for rectified linear unit (ReLU) networks. In this paper, we prove a variant of the relevant dynamical systems result, a center-stable manifold theorem, in which we relax some of the regularity requirements. Then, we verify that shallow ReLU networks fit into the new framework. Building on a classification of critical points of the square integral loss of shallow ReLU networks measured against an affine target function, we deduce that gradient descent avoids most saddle points. We proceed to prove convergence to global minima if the initialization is sufficiently good, which is expressed by an explicit threshold on the limiting loss.

Computation of conditional expectations with guarantees

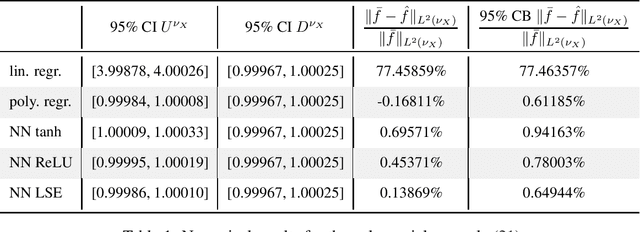
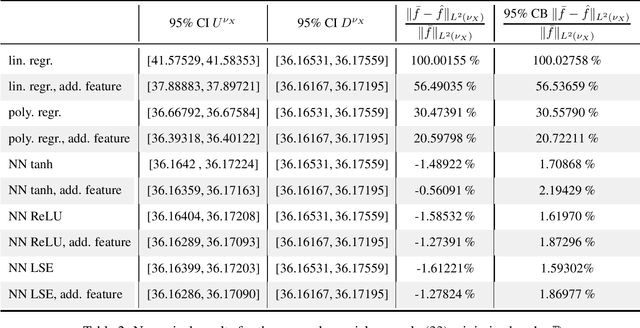
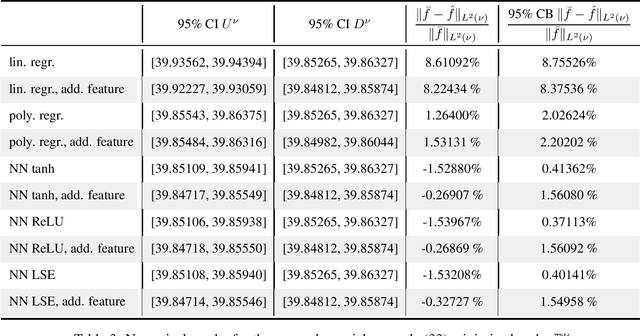
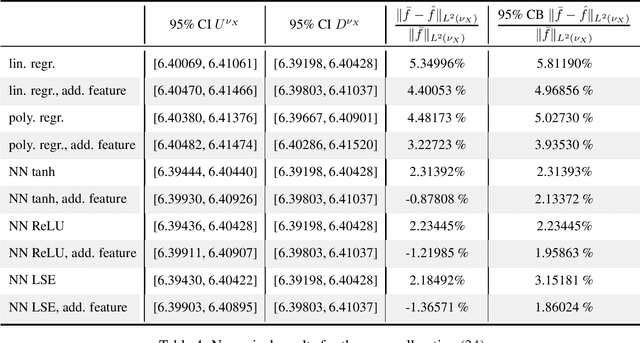
Theoretically, the conditional expectation of a square-integrable random variable $Y$ given a $d$-dimensional random vector $X$ can be obtained by minimizing the mean squared distance between $Y$ and $f(X)$ over all Borel measurable functions $f \colon \mathbb{R}^d \to \mathbb{R}$. However, in many applications this minimization problem cannot be solved exactly, and instead, a numerical method that computes an approximate minimum over a suitable subfamily of Borel functions has to be used. The quality of the result depends on the adequacy of the subfamily and the performance of the numerical method. In this paper, we derive an expected value representation of the minimal mean square distance which in many applications can efficiently be approximated with a standard Monte Carlo average. This enables us to provide guarantees for the accuracy of any numerical approximation of a given conditional expectation. We illustrate the method by assessing the quality of approximate conditional expectations obtained by linear, polynomial as well as neural network regression in different concrete examples.

Landscape analysis for shallow ReLU neural networks: complete classification of critical points for affine target functions

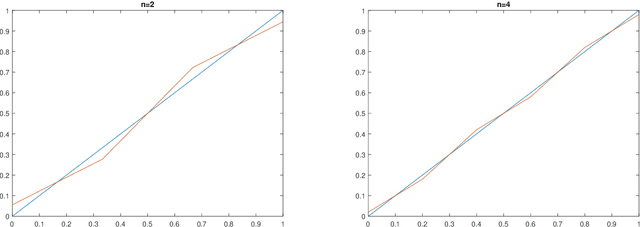
In this paper, we analyze the landscape of the true loss of a ReLU neural network with one hidden layer. We provide a complete classification of the critical points in the case where the target function is affine. In particular, we prove that local minima and saddle points have to be of a special form and show that there are no local maxima. Our approach is of a combinatorial nature and builds on a careful analysis of the different types of hidden neurons that can occur in a ReLU neural network.

A proof of convergence for gradient descent in the training of artificial neural networks for constant target functions

Gradient descent optimization algorithms are the standard ingredients that are used to train artificial neural networks (ANNs). Even though a huge number of numerical simulations indicate that gradient descent optimization methods do indeed convergence in the training of ANNs, until today there is no rigorous theoretical analysis which proves (or disproves) this conjecture. In particular, even in the case of the most basic variant of gradient descent optimization algorithms, the plain vanilla gradient descent method, it remains an open problem to prove or disprove the conjecture that gradient descent converges in the training of ANNs. In this article we solve this problem in the special situation where the target function under consideration is a constant function. More specifically, in the case of constant target functions we prove in the training of rectified fully-connected feedforward ANNs with one-hidden layer that the risk function of the gradient descent method does indeed converge to zero. Our mathematical analysis strongly exploits the property that the rectifier function is the activation function used in the considered ANNs. A key contribution of this work is to explicitly specify a Lyapunov function for the gradient flow system of the ANN parameters. This Lyapunov function is the central tool in our convergence proof of the gradient descent method.

Deep learning based numerical approximation algorithms for stochastic partial differential equations and high-dimensional nonlinear filtering problems

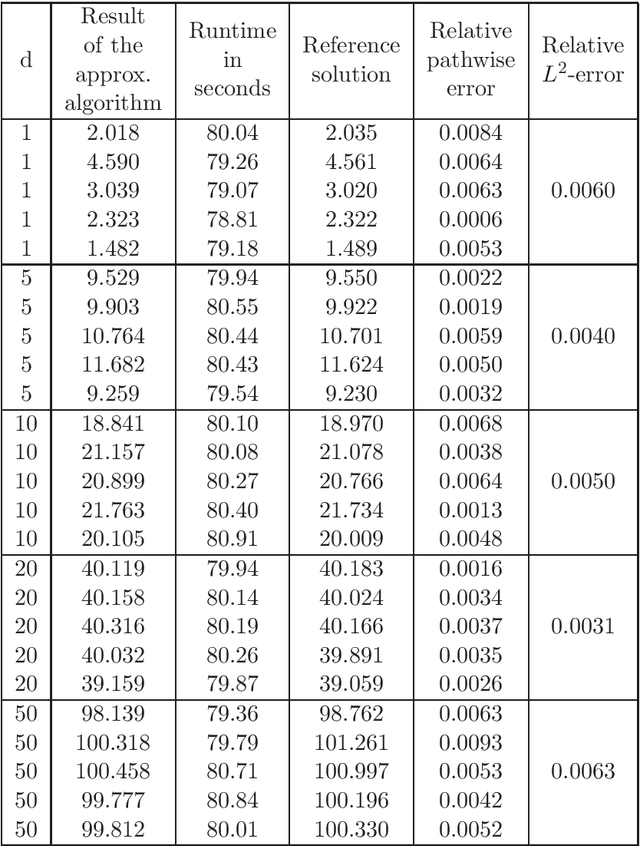
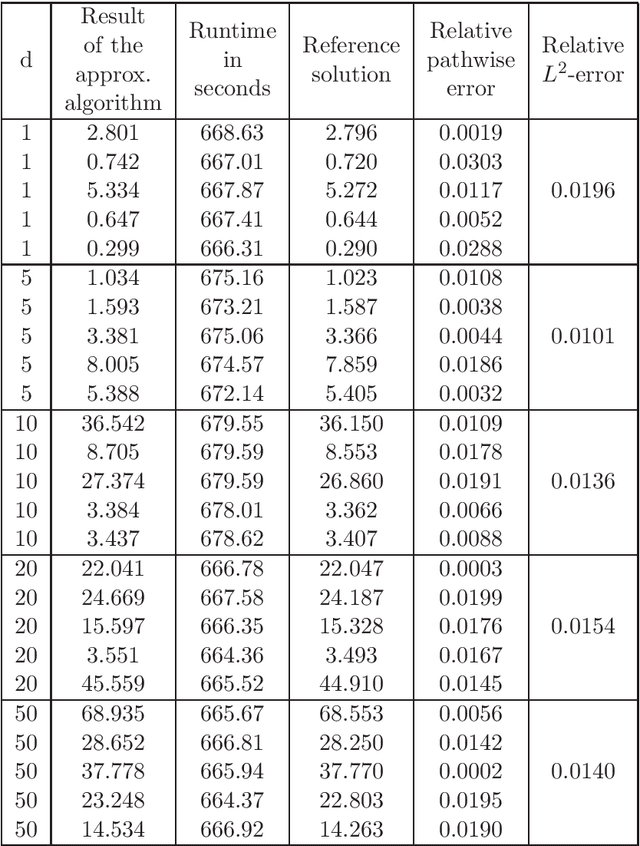
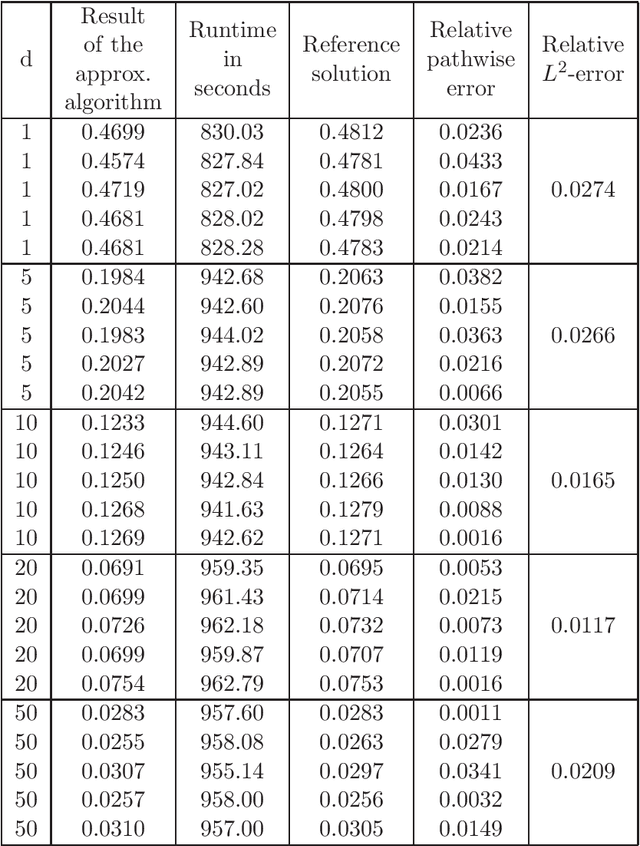
In this article we introduce and study a deep learning based approximation algorithm for solutions of stochastic partial differential equations (SPDEs). In the proposed approximation algorithm we employ a deep neural network for every realization of the driving noise process of the SPDE to approximate the solution process of the SPDE under consideration. We test the performance of the proposed approximation algorithm in the case of stochastic heat equations with additive noise, stochastic heat equations with multiplicative noise, stochastic Black--Scholes equations with multiplicative noise, and Zakai equations from nonlinear filtering. In each of these SPDEs the proposed approximation algorithm produces accurate results with short run times in up to 50 space dimensions.

Non-convergence of stochastic gradient descent in the training of deep neural networks

Deep neural networks have successfully been trained in various application areas with stochastic gradient descent. However, there exists no rigorous mathematical explanation why this works so well. The training of neural networks with stochastic gradient descent has four different discretization parameters: (i) the network architecture; (ii) the size of the training data; (iii) the number of gradient steps; and (iv) the number of randomly initialized gradient trajectories. While it can be shown that the approximation error converges to zero if all four parameters are sent to infinity in the right order, we demonstrate in this paper that stochastic gradient descent fails to converge for rectified linear unit networks if their depth is much larger than their width and the number of random initializations does not increase to infinity fast enough.

Solving high-dimensional optimal stopping problems using deep learning

Nowadays many financial derivatives which are traded on stock and futures exchanges, such as American or Bermudan options, are of early exercise type. Often the pricing of early exercise options gives rise to high-dimensional optimal stopping problems, since the dimension corresponds to the number of underlyings in the associated hedging portfolio. High-dimensional optimal stopping problems are, however, notoriously difficult to solve due to the well-known curse of dimensionality. In this work we propose an algorithm for solving such problems, which is based on deep learning and computes, in the context of early exercise option pricing, both approximations for an optimal exercise strategy and the price of the considered option. The proposed algorithm can also be applied to optimal stopping problems that arise in other areas where the underlying stochastic process can be efficiently simulated. We present numerical results for a large number of example problems, which include the pricing of many high-dimensional American and Bermudan options such as, for example, Bermudan max-call options in up to 5000 dimensions. Most of the obtained results are compared to reference values computed by exploiting the specific problem design or, where available, to reference values from the literature. These numerical results suggest that the proposed algorithm is highly effective in the case of many underlyings, in terms of both accuracy and speed.

Deep splitting method for parabolic PDEs

In this paper we introduce a numerical method for parabolic PDEs that combines operator splitting with deep learning. It divides the PDE approximation problem into a sequence of separate learning problems. Since the computational graph for each of the subproblems is comparatively small, the approach can handle extremely high-dimensional PDEs. We test the method on different examples from physics, stochastic control, and mathematical finance. In all cases, it yields very good results in up to 10,000 dimensions with short run times.