A Multi-directional Meta-Learning Framework for Class-Generalizable Anomaly Detection

In this paper, we address the problem of class-generalizable anomaly detection, where the objective is to develop a unified model by focusing our learning on the available normal data and a small amount of anomaly data in order to detect the completely unseen anomalies, also referred to as the out-of-distribution (OOD) classes. Adding to this challenge is the fact that the anomaly data is rare and costly to label. To achieve this, we propose a multidirectional meta-learning algorithm -- at the inner level, the model aims to learn the manifold of the normal data (representation); at the outer level, the model is meta-tuned with a few anomaly samples to maximize the softmax confidence margin between the normal and anomaly samples (decision surface calibration), treating normals as in-distribution (ID) and anomalies as out-of-distribution (OOD). By iteratively repeating this process over multiple episodes of predominantly normal and a small number of anomaly samples, we realize a multidirectional meta-learning framework. This two-level optimization, enhanced by multidirectional training, enables stronger generalization to unseen anomaly classes.

Beyond Marginals: Learning Joint Spatio-Temporal Patterns for Multivariate Anomaly Detection

In this paper, we aim to improve multivariate anomaly detection (AD) by modeling the \textit{time-varying non-linear spatio-temporal correlations} found in multivariate time series data . In multivariate time series data, an anomaly may be indicated by the simultaneous deviation of interrelated time series from their expected collective behavior, even when no individual time series exhibits a clearly abnormal pattern on its own. In many existing approaches, time series variables are assumed to be (conditionally) independent, which oversimplifies real-world interactions. Our approach addresses this by modeling joint dependencies in the latent space and decoupling the modeling of \textit{marginal distributions, temporal dynamics, and inter-variable dependencies}. We use a transformer encoder to capture temporal patterns, and to model spatial (inter-variable) dependencies, we fit a multi-variate likelihood and a copula. The temporal and the spatial components are trained jointly in a latent space using a self-supervised contrastive learning objective to learn meaningful feature representations to separate normal and anomaly samples.

Improving Intrusion Detection with Domain-Invariant Representation Learning in Latent Space

Domain generalization focuses on leveraging knowledge from multiple related domains with ample training data and labels to enhance inference on unseen in-distribution (IN) and out-of-distribution (OOD) domains. In our study, we introduce a two-phase representation learning technique using multi-task learning. This approach aims to cultivate a latent space from features spanning multiple domains, encompassing both native and cross-domains, to amplify generalization to IN and OOD territories. Additionally, we attempt to disentangle the latent space by minimizing the mutual information between the prior and latent space, effectively de-correlating spurious feature correlations. Collectively, the joint optimization will facilitate domain-invariant feature learning. We assess the model's efficacy across multiple cybersecurity datasets, using standard classification metrics on both unseen IN and OOD sets, and juxtapose the results with contemporary domain generalization methods.

Deep Correlation-Aware Kernelized Autoencoders for Anomaly Detection in Cybersecurity

Unsupervised learning-based anomaly detection in latent space has gained importance since discriminating anomalies from normal data becomes difficult in high-dimensional space. Both density estimation and distance-based methods to detect anomalies in latent space have been explored in the past. These methods prove that retaining valuable properties of input data in latent space helps in the better reconstruction of test data. Moreover, real-world sensor data is skewed and non-Gaussian in nature, making mean-based estimators unreliable for skewed data. Again, anomaly detection methods based on reconstruction error rely on Euclidean distance, which does not consider useful correlation information in the feature space and also fails to accurately reconstruct the data when it deviates from the training distribution. In this work, we address the limitations of reconstruction error-based autoencoders and propose a kernelized autoencoder that leverages a robust form of Mahalanobis distance (MD) to measure latent dimension correlation to effectively detect both near and far anomalies. This hybrid loss is aided by the principle of maximizing the mutual information gain between the latent dimension and the high-dimensional prior data space by maximizing the entropy of the latent space while preserving useful correlation information of the original data in the low-dimensional latent space. The multi-objective function has two goals -- it measures correlation information in the latent feature space in the form of robust MD distance and simultaneously tries to preserve useful correlation information from the original data space in the latent space by maximizing mutual information between the prior and latent space.

Deep diffusion-based forecasting of COVID-19 by incorporating network-level mobility information

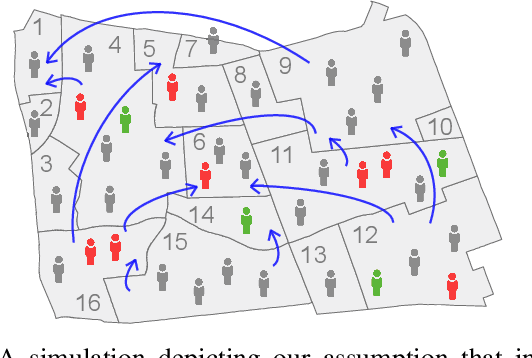
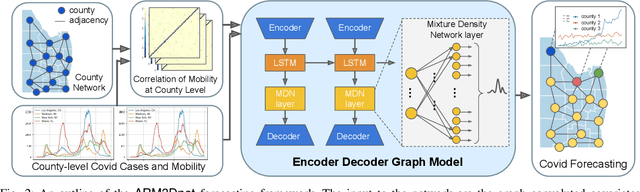
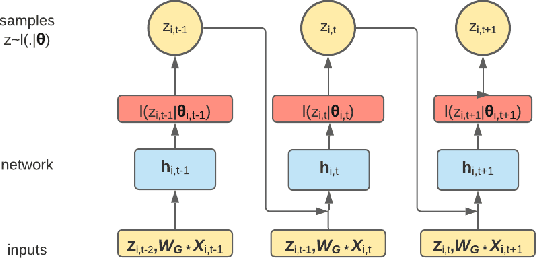
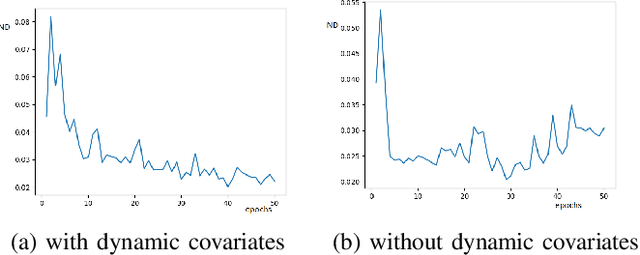
Modeling the spatiotemporal nature of the spread of infectious diseases can provide useful intuition in understanding the time-varying aspect of the disease spread and the underlying complex spatial dependency observed in people's mobility patterns. Besides, the county level multiple related time series information can be leveraged to make a forecast on an individual time series. Adding to this challenge is the fact that real-time data often deviates from the unimodal Gaussian distribution assumption and may show some complex mixed patterns. Motivated by this, we develop a deep learning-based time-series model for probabilistic forecasting called Auto-regressive Mixed Density Dynamic Diffusion Network(ARM3Dnet), which considers both people's mobility and disease spread as a diffusion process on a dynamic directed graph. The Gaussian Mixture Model layer is implemented to consider the multimodal nature of the real-time data while learning from multiple related time series. We show that our model, when trained with the best combination of dynamic covariate features and mixture components, can outperform both traditional statistical and deep learning models in forecasting the number of Covid-19 deaths and cases at the county level in the United States.