Ranking Items from Discrete Ratings: The Cost of Unknown User Thresholds

Ranking items is a central task in many information retrieval and recommender systems. User input for the ranking task often comes in the form of ratings on a coarse discrete scale. We ask whether it is possible to recover a fine-grained item ranking from such coarse-grained ratings. We model items as having scores and users as having thresholds; a user rates an item positively if the item's score exceeds the user's threshold. Although all users agree on the total item order, estimating that order is challenging when both the scores and the thresholds are latent. Under our model, any ranking method naturally partitions the $n$ items into bins; the bins are ordered, but the items inside each bin are still unordered. Users arrive sequentially, and every new user can be queried to refine the current ranking. We prove that achieving a near-perfect ranking, measured by Spearman distance, requires $\Theta(n^2)$ users (and therefore $\Omega(n^2)$ queries). This is significantly worse than the $O(n\log n)$ queries needed to rank from comparisons; the gap reflects the additional queries needed to identify the users who have the appropriate thresholds. Our bound also quantifies the impact of a mismatch between score and threshold distributions via a quadratic divergence factor. To show the tightness of our results, we provide a ranking algorithm whose query complexity matches our bound up to a logarithmic factor. Our work reveals a tension in online ranking: diversity in thresholds is necessary to merge coarse ratings from many users into a fine-grained ranking, but this diversity has a cost if the thresholds are a priori unknown.

An Equivalence Between Data Poisoning and Byzantine Gradient Attacks

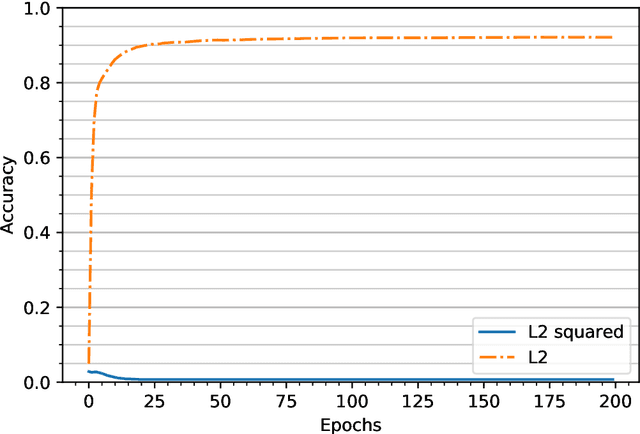
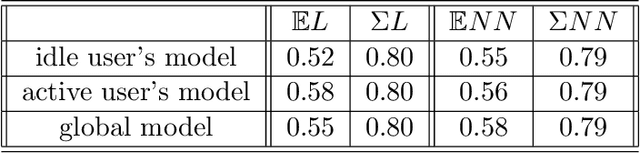
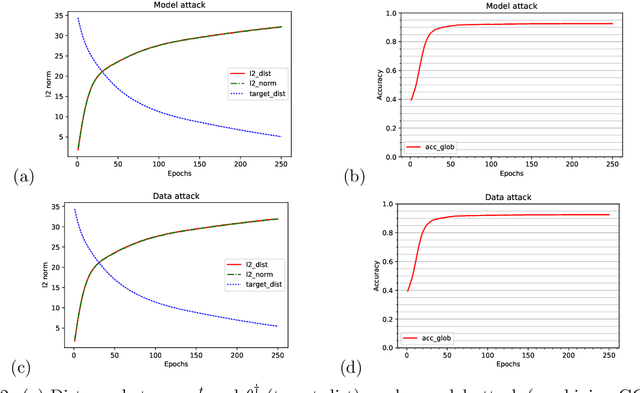
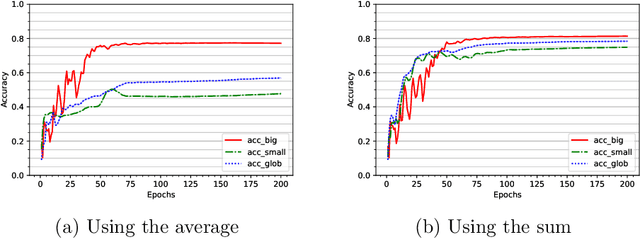
To study the resilience of distributed learning, the "Byzantine" literature considers a strong threat model where workers can report arbitrary gradients to the parameter server. Whereas this model helped obtain several fundamental results, it has sometimes been considered unrealistic, when the workers are mostly trustworthy machines. In this paper, we show a surprising equivalence between this model and data poisoning, a threat considered much more realistic. More specifically, we prove that every gradient attack can be reduced to data poisoning, in any personalized federated learning system with PAC guarantees (which we show are both desirable and realistic). This equivalence makes it possible to obtain new impossibility results on the resilience to data poisoning as corollaries of existing impossibility theorems on Byzantine machine learning. Moreover, using our equivalence, we derive a practical attack that we show (theoretically and empirically) can be very effective against classical personalized federated learning models.