Constrained Bayesian Inference for Low Rank Multitask Learning

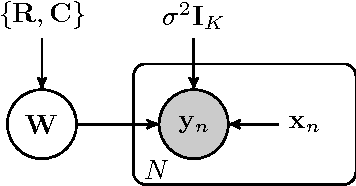
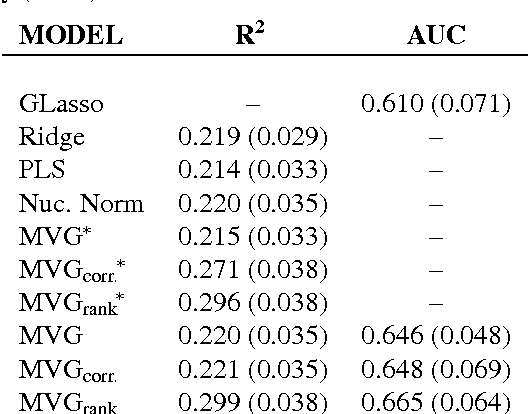
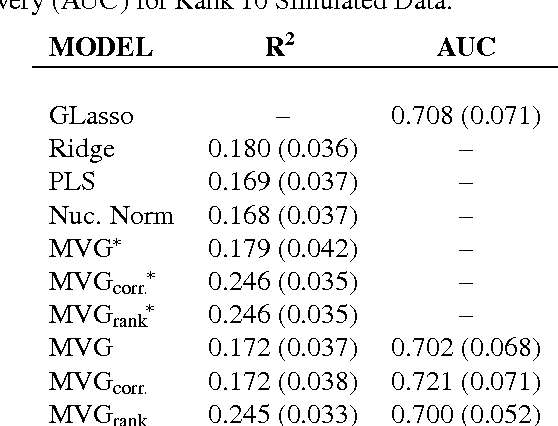
We present a novel approach for constrained Bayesian inference. Unlike current methods, our approach does not require convexity of the constraint set. We reduce the constrained variational inference to a parametric optimization over the feasible set of densities and propose a general recipe for such problems. We apply the proposed constrained Bayesian inference approach to multitask learning subject to rank constraints on the weight matrix. Further, constrained parameter estimation is applied to recover the sparse conditional independence structure encoded by prior precision matrices. Our approach is motivated by reverse inference for high dimensional functional neuroimaging, a domain where the high dimensionality and small number of examples requires the use of constraints to ensure meaningful and effective models. For this application, we propose a model that jointly learns a weight matrix and the prior inverse covariance structure between different tasks. We present experimental validation showing that the proposed approach outperforms strong baseline models in terms of predictive performance and structure recovery.

The trace norm constrained matrix-variate Gaussian process for multitask bipartite ranking

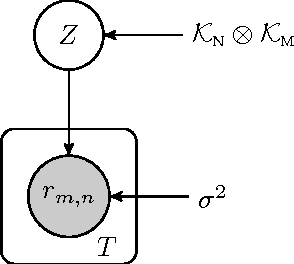
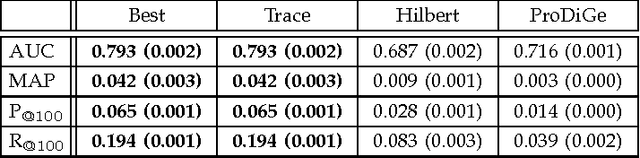
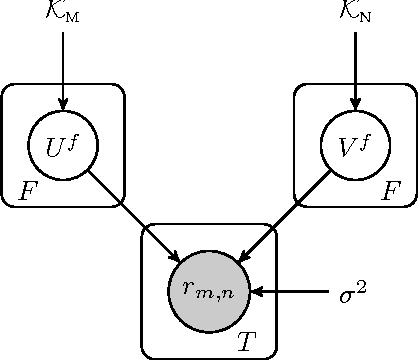
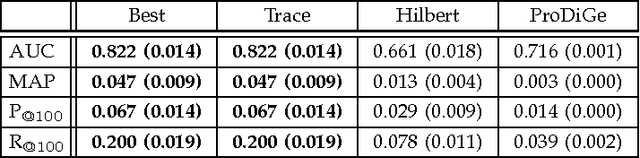
We propose a novel hierarchical model for multitask bipartite ranking. The proposed approach combines a matrix-variate Gaussian process with a generative model for task-wise bipartite ranking. In addition, we employ a novel trace constrained variational inference approach to impose low rank structure on the posterior matrix-variate Gaussian process. The resulting posterior covariance function is derived in closed form, and the posterior mean function is the solution to a matrix-variate regression with a novel spectral elastic net regularizer. Further, we show that variational inference for the trace constrained matrix-variate Gaussian process combined with maximum likelihood parameter estimation for the bipartite ranking model is jointly convex. Our motivating application is the prioritization of candidate disease genes. The goal of this task is to aid the identification of unobserved associations between human genes and diseases using a small set of observed associations as well as kernels induced by gene-gene interaction networks and disease ontologies. Our experimental results illustrate the performance of the proposed model on real world datasets. Moreover, we find that the resulting low rank solution improves the computational scalability of training and testing as compared to baseline models.

Learning to Rank With Bregman Divergences and Monotone Retargeting

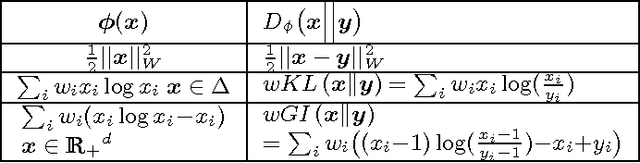
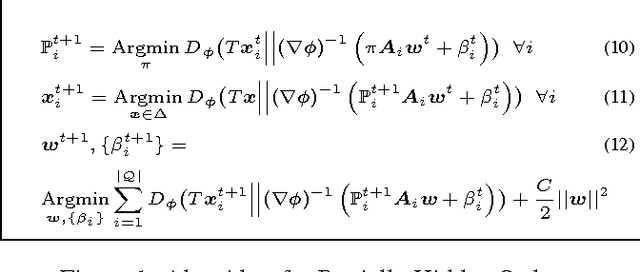
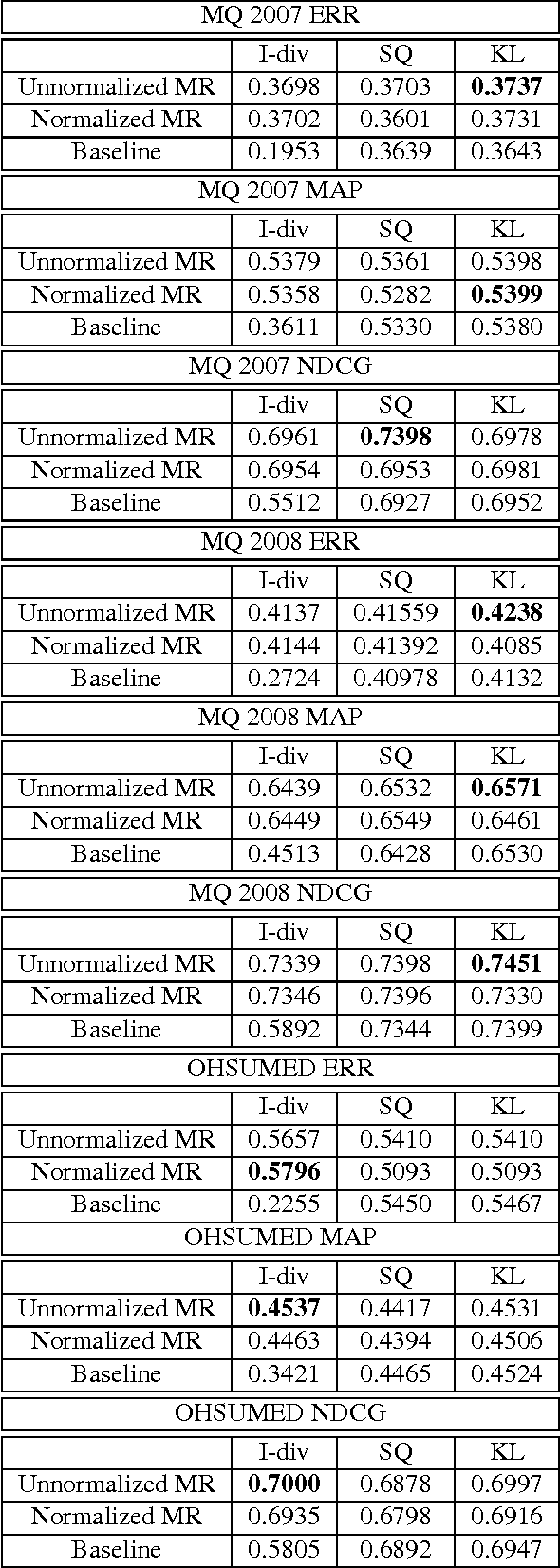
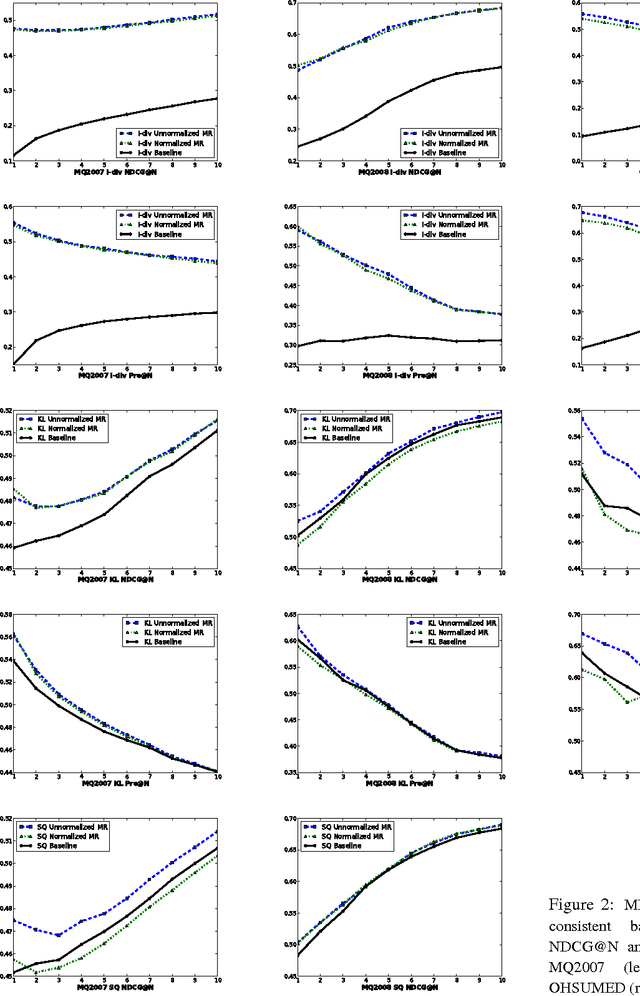
This paper introduces a novel approach for learning to rank (LETOR) based on the notion of monotone retargeting. It involves minimizing a divergence between all monotonic increasing transformations of the training scores and a parameterized prediction function. The minimization is both over the transformations as well as over the parameters. It is applied to Bregman divergences, a large class of "distance like" functions that were recently shown to be the unique class that is statistically consistent with the normalized discounted gain (NDCG) criterion [19]. The algorithm uses alternating projection style updates, in which one set of simultaneous projections can be computed independent of the Bregman divergence and the other reduces to parameter estimation of a generalized linear model. This results in easily implemented, efficiently parallelizable algorithm for the LETOR task that enjoys global optimum guarantees under mild conditions. We present empirical results on benchmark datasets showing that this approach can outperform the state of the art NDCG consistent techniques.