Towards Realistic Individual Recourse and Actionable Explanations in Black-Box Decision Making Systems

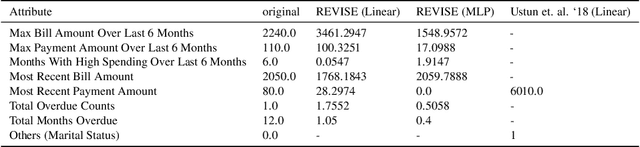
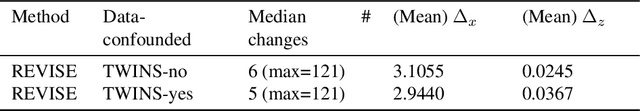
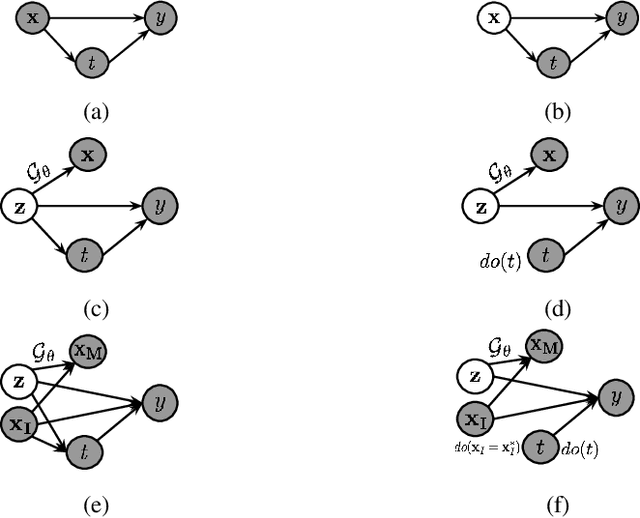
Machine learning based decision making systems are increasingly affecting humans. An individual can suffer an undesirable outcome under such decision making systems (e.g. denied credit) irrespective of whether the decision is fair or accurate. Individual recourse pertains to the problem of providing an actionable set of changes a person can undertake in order to improve their outcome. We propose a recourse algorithm that models the underlying data distribution or manifold. We then provide a mechanism to generate the smallest set of changes that will improve an individual's outcome. This mechanism can be easily used to provide recourse for any differentiable machine learning based decision making system. Further, the resulting algorithm is shown to be applicable to both supervised classification and causal decision making systems. Our work attempts to fill gaps in existing fairness literature that have primarily focused on discovering and/or algorithmically enforcing fairness constraints on decision making systems. This work also provides an alternative approach to generating counterfactual explanations.

Partially Linear Additive Gaussian Graphical Models

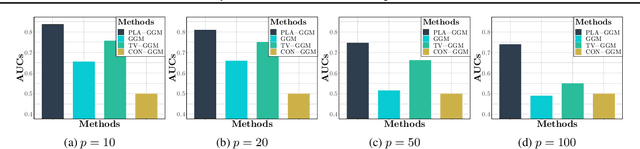
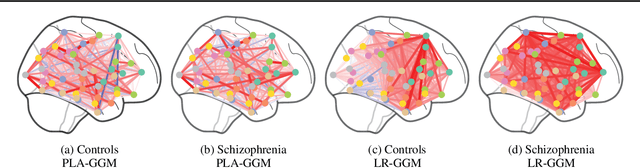
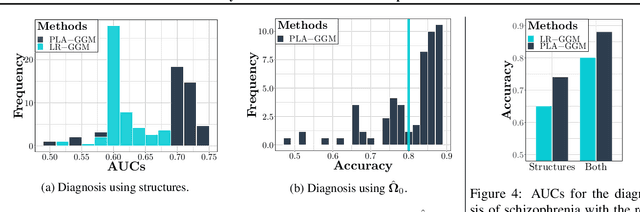
We propose a partially linear additive Gaussian graphical model (PLA-GGM) for the estimation of associations between random variables distorted by observed confounders. Model parameters are estimated using an $L_1$-regularized maximal pseudo-profile likelihood estimator (MaPPLE) for which we prove $\sqrt{n}$-sparsistency. Importantly, our approach avoids parametric constraints on the effects of confounders on the estimated graphical model structure. Empirically, the PLA-GGM is applied to both synthetic and real-world datasets, demonstrating superior performance compared to competing methods.

Clustered Monotone Transforms for Rating Factorization

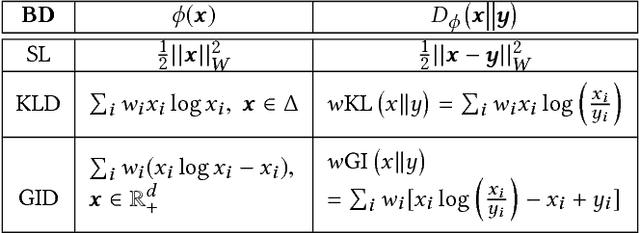
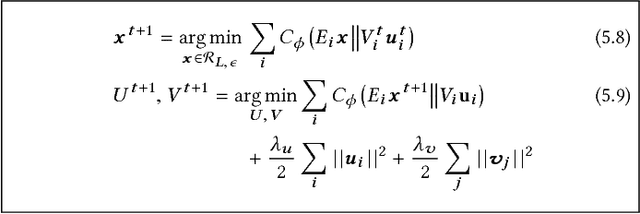
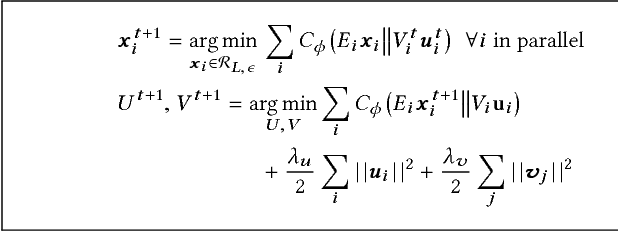
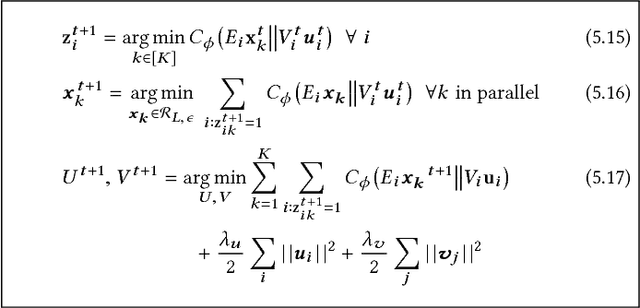
Exploiting low-rank structure of the user-item rating matrix has been the crux of many recommendation engines. However, existing recommendation engines force raters with heterogeneous behavior profiles to map their intrinsic rating scales to a common rating scale (e.g. 1-5). This non-linear transformation of the rating scale shatters the low-rank structure of the rating matrix, therefore resulting in a poor fit and consequentially, poor recommendations. In this paper, we propose Clustered Monotone Transforms for Rating Factorization (CMTRF), a novel approach to perform regression up to unknown monotonic transforms over unknown population segments. Essentially, for recommendation systems, the technique searches for monotonic transformations of the rating scales resulting in a better fit. This is combined with an underlying matrix factorization regression model that couples the user-wise ratings to exploit shared low dimensional structure. The rating scale transformations can be generated for each user, for a cluster of users, or for all the users at once, forming the basis of three simple and efficient algorithms proposed in this paper, all of which alternate between transformation of the rating scales and matrix factorization regression. Despite the non-convexity, CMTRF is theoretically shown to recover a unique solution under mild conditions. Experimental results on two synthetic and seven real-world datasets show that CMTRF outperforms other state-of-the-art baselines.

Interpreting Black Box Predictions using Fisher Kernels

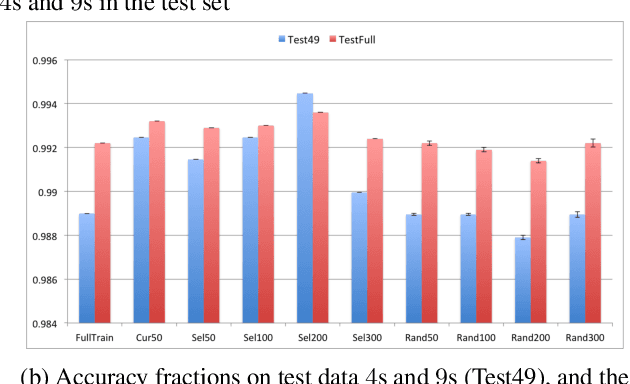
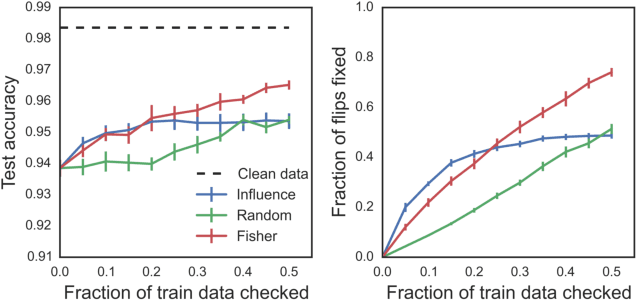
Research in both machine learning and psychology suggests that salient examples can help humans to interpret learning models. To this end, we take a novel look at black box interpretation of test predictions in terms of training examples. Our goal is to ask `which training examples are most responsible for a given set of predictions'? To answer this question, we make use of Fisher kernels as the defining feature embedding of each data point, combined with Sequential Bayesian Quadrature (SBQ) for efficient selection of examples. In contrast to prior work, our method is able to seamlessly handle any sized subset of test predictions in a principled way. We theoretically analyze our approach, providing novel convergence bounds for SBQ over discrete candidate atoms. Our approach recovers the application of influence functions for interpretability as a special case yielding novel insights from this connection. We also present applications of the proposed approach to three use cases: cleaning training data, fixing mislabeled examples and data summarization.

Joint Nonparametric Precision Matrix Estimation with Confounding

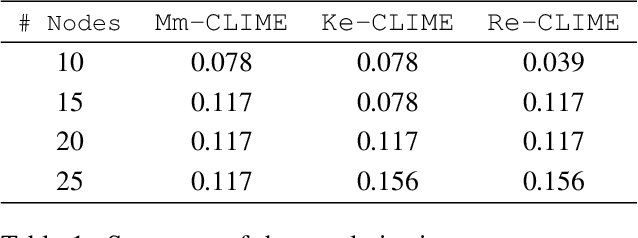
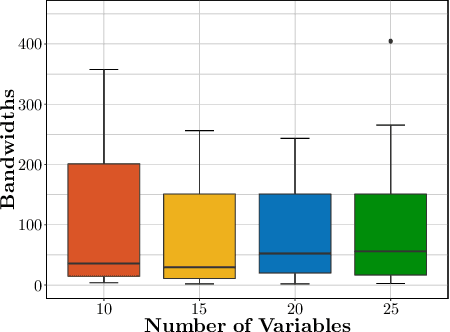
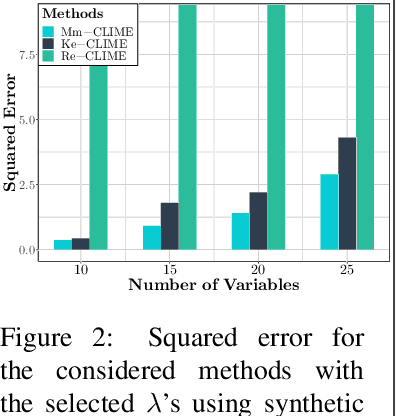
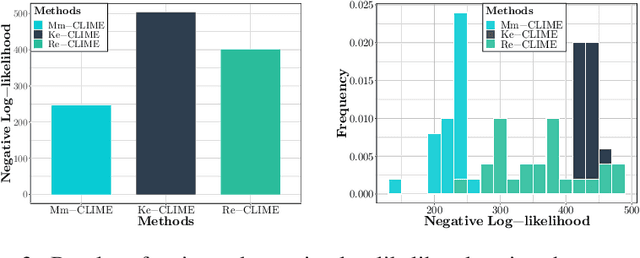
We consider the problem of precision matrix estimation where, due to extraneous confounding of the underlying precision matrix, the data are independent but not identically distributed. While such confounding occurs in many scientific problems, our approach is inspired by recent neuroscientific research suggesting that brain function, as measured using functional magnetic resonance imagine (fMRI), is susceptible to confounding by physiological noise such as breathing and subject motion. Following the scientific motivation, we propose a graphical model, which in turn motivates a joint nonparametric estimator. We provide theoretical guarantees for the consistency and the convergence rate of the proposed estimator. In addition, we demonstrate that the optimization of the proposed estimator can be transformed into a series of linear programming problems, and thus be efficiently solved in parallel. Empirical results are presented using simulated and real brain imaging data, which suggest that our approach improves precision matrix estimation, as compared to baselines, when confounding is present.

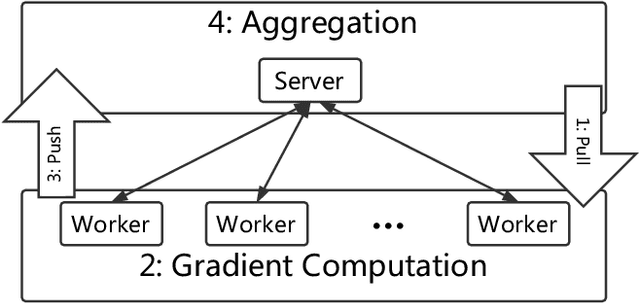
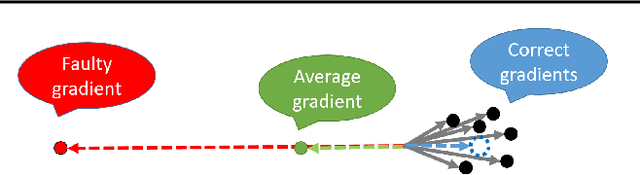
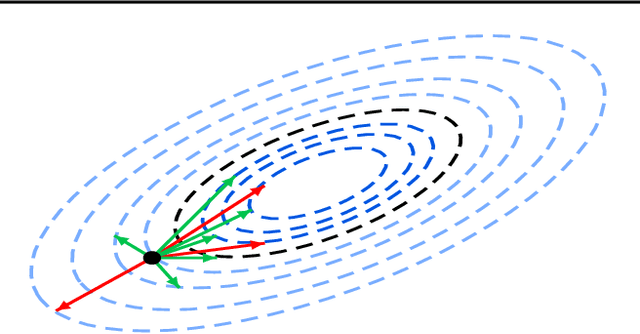
Zeno: Byzantine-suspicious stochastic gradient descent

We propose Zeno, a new robust aggregation rule, for distributed synchronous Stochastic Gradient Descent~(SGD) under a general Byzantine failure model. The key idea is to suspect the workers that are potentially malicious, and use a ranking-based preference mechanism. This allows us to generalize beyond past work--in our case, the number of malicious workers can be arbitrarily large, and we use only the weakest assumption on honest workers~(at least one honest worker). We prove the convergence of SGD under these scenarios. Empirical results show that Zeno outperforms existing approaches under various attacks.

xGEMs: Generating Examplars to Explain Black-Box Models

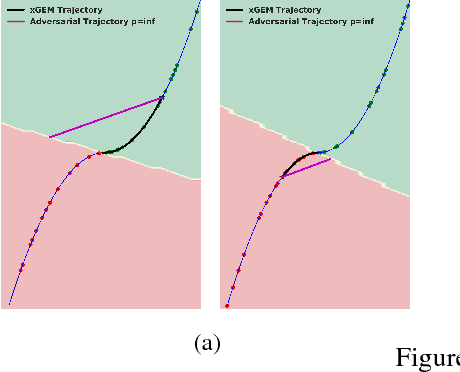
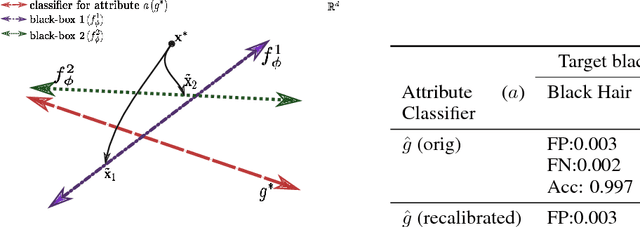
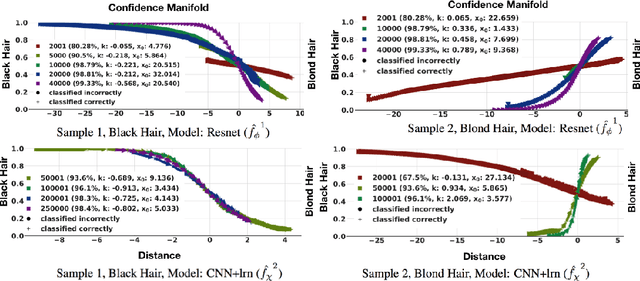
This work proposes xGEMs or manifold guided exemplars, a framework to understand black-box classifier behavior by exploring the landscape of the underlying data manifold as data points cross decision boundaries. To do so, we train an unsupervised implicit generative model -- treated as a proxy to the data manifold. We summarize black-box model behavior quantitatively by perturbing data samples along the manifold. We demonstrate xGEMs' ability to detect and quantify bias in model learning and also for understanding the changes in model behavior as training progresses.

Eliciting Binary Performance Metrics

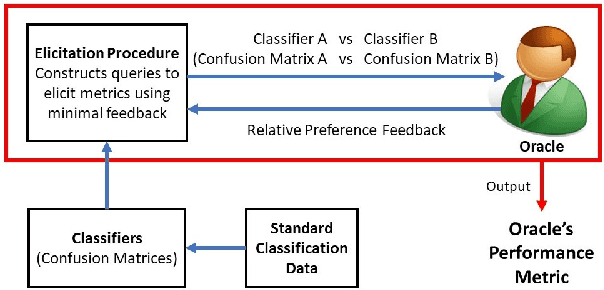
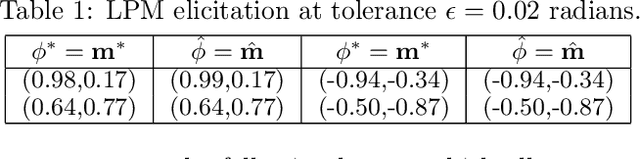
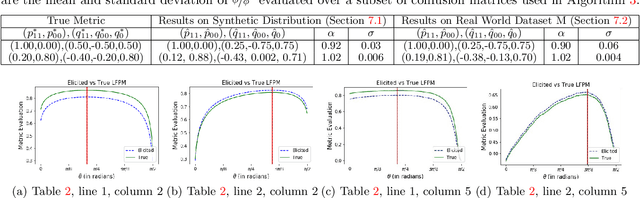
Given a binary prediction problem, which performance metric should the classifier optimize? We address this question by formalizing the problem of metric elicitation. In particular, we focus on eliciting binary performance metrics from pairwise preferences, where users provide relative feedback for pairs of classifiers. By exploiting key properties of the space of confusion matrices, we obtain provably query efficient algorithms for eliciting linear and linear-fractional metrics. We further show that our method is robust to feedback and finite sample noise.

Binary Classification with Karmic, Threshold-Quasi-Concave Metrics

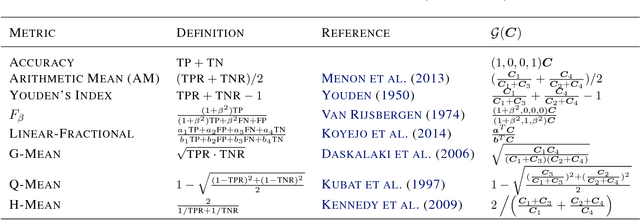
Complex performance measures, beyond the popular measure of accuracy, are increasingly being used in the context of binary classification. These complex performance measures are typically not even decomposable, that is, the loss evaluated on a batch of samples cannot typically be expressed as a sum or average of losses evaluated at individual samples, which in turn requires new theoretical and methodological developments beyond standard treatments of supervised learning. In this paper, we advance this understanding of binary classification for complex performance measures by identifying two key properties: a so-called Karmic property, and a more technical threshold-quasi-concavity property, which we show is milder than existing structural assumptions imposed on performance measures. Under these properties, we show that the Bayes optimal classifier is a threshold function of the conditional probability of positive class. We then leverage this result to come up with a computationally practical plug-in classifier, via a novel threshold estimator, and further, provide a novel statistical analysis of classification error with respect to complex performance measures.

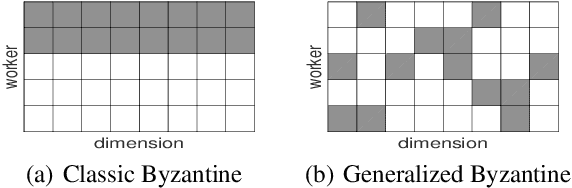
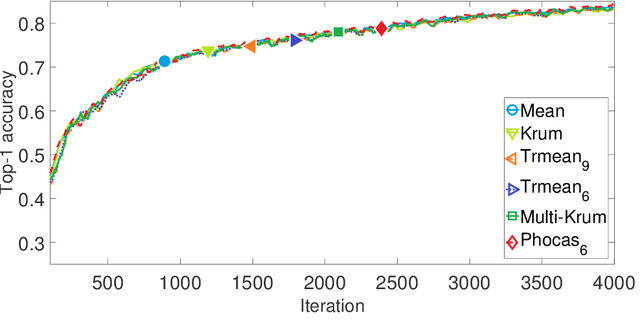
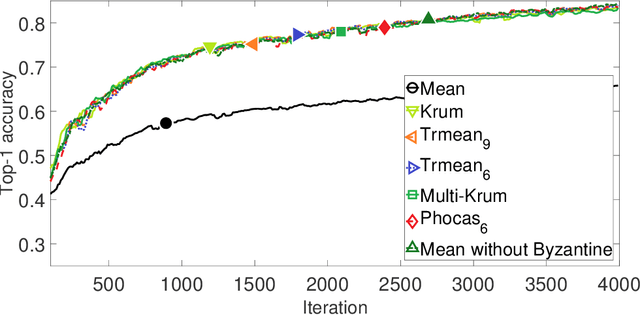
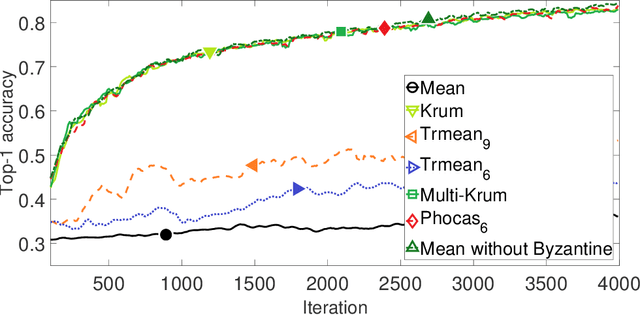
Phocas: dimensional Byzantine-resilient stochastic gradient descent

We propose a novel robust aggregation rule for distributed synchronous Stochastic Gradient Descent~(SGD) under a general Byzantine failure model. The attackers can arbitrarily manipulate the data transferred between the servers and the workers in the parameter server~(PS) architecture. We prove the Byzantine resilience of the proposed aggregation rules. Empirical analysis shows that the proposed techniques outperform current approaches for realistic use cases and Byzantine attack scenarios.