Vision-Based Runtime Monitoring under Varying Specifications using Semantic Latent Representations

We study certified runtime monitoring of past-time signal temporal logic (ptSTL) from visual observations under partial observability. The monitor must infer safety-relevant quantities from images and provide finite-sample guarantees, while being \emph{reusable}: once trained and calibrated, it should certify any formula in a target fragment without per-formula retraining. For fragments induced by a finite dictionary of temporal atoms, we prove that the \emph{semantic basis}, the vector of atom robustness scores, is the minimum prediction target within the class of monotone, 1-Lipschitz reusable interfaces: any formula is evaluated by a deterministic decoder derived from the parse tree, and a single conformal calibration pass certifies the entire fragment with no union bound. We also introduce a \emph{rolling prediction monitor} that predicts only current predicate values and reconstructs temporal history online; this is easier to learn but grows conservative at long horizons. On a pedestrian-crossroad benchmark, rolling achieves tighter certified bounds at short horizons while the semantic-basis monitor is up to 4-times tighter at long horizons. We validate the presented monitors on real-world Waymo driving data, where both monitors satisfy the conformal coverage guarantee empirically.

Safety Certification is Classification

The goal of this paper is certifying safety of dynamical systems subject to uncertainty. Existing approaches use trajectory data to estimate transition probabilities, and compute safety probabilities recursively via dynamic programming (DP). This recursion may lead to compounding errors in the certified safety probability, thus collapsing to a vacuous lower bound for growing horizons $T$. We propose a kernel embedding framework that treats safety certification as a classification problem on trajectory data, directly estimating the $T$-step safety probability without recursion. We show that the framework subsumes well-established approaches from the literature (e.g., barrier certificates, robust Markov models) as special cases, and allows us to go beyond their limitations. As the main consequence, it bypasses compounding error across the horizon and enables certification for systems with non-Markovian dynamics. We demonstrate that direct estimators remain stable independent of the certification horizon and in the non-Markovian setting, whilst DP-based certificates silently go unsound -- confirmed in simulation on a neural-controlled quadrotor.

Kernel-Based Learning of Safety Barriers

The rapid integration of AI algorithms in safety-critical applications such as autonomous driving and healthcare is raising significant concerns about the ability to meet stringent safety standards. Traditional tools for formal safety verification struggle with the black-box nature of AI-driven systems and lack the flexibility needed to scale to the complexity of real-world applications. In this paper, we present a data-driven approach for safety verification and synthesis of black-box systems with discrete-time stochastic dynamics. We employ the concept of control barrier certificates, which can guarantee safety of the system, and learn the certificate directly from a set of system trajectories. We use conditional mean embeddings to embed data from the system into a reproducing kernel Hilbert space (RKHS) and construct an RKHS ambiguity set that can be inflated to robustify the result to out-of-distribution behavior. We provide the theoretical results on how to apply the approach to general classes of temporal logic specifications beyond safety. For the data-driven computation of safety barriers, we leverage a finite Fourier expansion to cast a typically intractable semi-infinite optimization problem as a linear program. The resulting spectral barrier allows us to leverage the fast Fourier transform to generate the relaxed problem efficiently, offering a scalable yet distributionally robust framework for verifying safety. Our work moves beyond restrictive assumptions on system dynamics and uncertainty, as demonstrated on two case studies including a black-box system with a neural network controller.

LUCID: Learning-Enabled Uncertainty-Aware Certification of Stochastic Dynamical Systems

Ensuring the safety of AI-enabled systems, particularly in high-stakes domains such as autonomous driving and healthcare, has become increasingly critical. Traditional formal verification tools fall short when faced with systems that embed both opaque, black-box AI components and complex stochastic dynamics. To address these challenges, we introduce LUCID (Learning-enabled Uncertainty-aware Certification of stochastIc Dynamical systems), a verification engine for certifying safety of black-box stochastic dynamical systems from a finite dataset of random state transitions. As such, LUCID is the first known tool capable of establishing quantified safety guarantees for such systems. Thanks to its modular architecture and extensive documentation, LUCID is designed for easy extensibility. LUCID employs a data-driven methodology rooted in control barrier certificates, which are learned directly from system transition data, to ensure formal safety guarantees. We use conditional mean embeddings to embed data into a reproducing kernel Hilbert space (RKHS), where an RKHS ambiguity set is constructed that can be inflated to robustify the result to out-of-distribution behavior. A key innovation within LUCID is its use of a finite Fourier kernel expansion to reformulate a semi-infinite non-convex optimization problem into a tractable linear program. The resulting spectral barrier allows us to leverage the fast Fourier transform to generate the relaxed problem efficiently, offering a scalable yet distributionally robust framework for verifying safety. LUCID thus offers a robust and efficient verification framework, able to handle the complexities of modern black-box systems while providing formal guarantees of safety. These unique capabilities are demonstrated on challenging benchmarks.

Data-Driven Distributionally Robust Safety Verification Using Barrier Certificates and Conditional Mean Embeddings

Algorithmic verification of realistic systems to satisfy safety and other temporal requirements has suffered from poor scalability of the employed formal approaches. To design systems with rigorous guarantees, many approaches still rely on exact models of the underlying systems. Since this assumption can rarely be met in practice, models have to be inferred from measurement data or are bypassed completely. Whilst former usually requires the model structure to be known a-priori and immense amounts of data to be available, latter gives rise to a plethora of restrictive mathematical assumptions about the unknown dynamics. In a pursuit of developing scalable formal verification algorithms without shifting the problem to unrealistic assumptions, we employ the concept of barrier certificates, which can guarantee safety of the system, and learn the certificate directly from a compact set of system trajectories. We use conditional mean embeddings to embed data from the system into a reproducing kernel Hilbert space (RKHS) and construct an RKHS ambiguity set that can be inflated to robustify the result w.r.t. a set of plausible transition kernels. We show how to solve the resulting program efficiently using sum-of-squares optimization and a Gaussian process envelope. Our approach lifts the need for restrictive assumptions on the system dynamics and uncertainty, and suggests an improvement in the sample complexity of verifying the safety of a system on a tested case study compared to a state-of-the-art approach.

Multi-Objective Physics-Guided Recurrent Neural Networks for Identifying Non-Autonomous Dynamical Systems

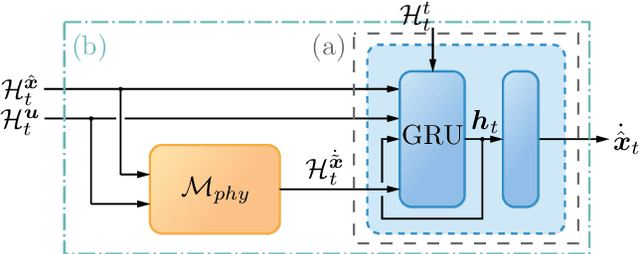
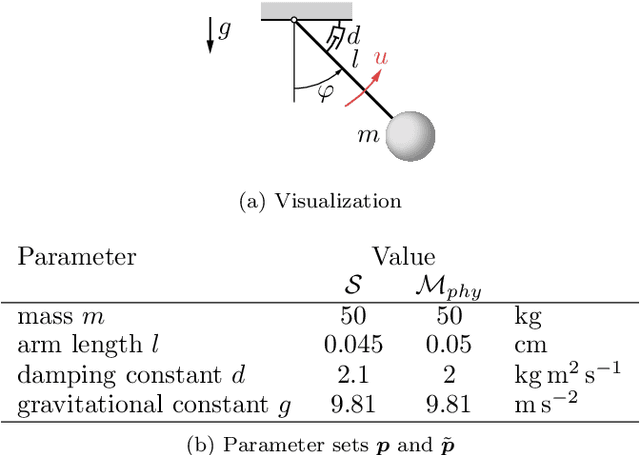
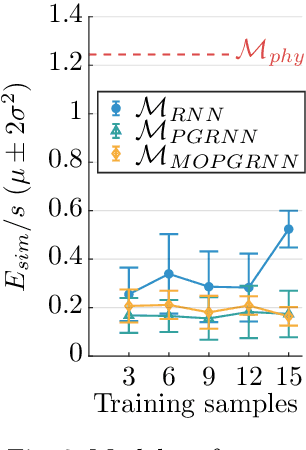
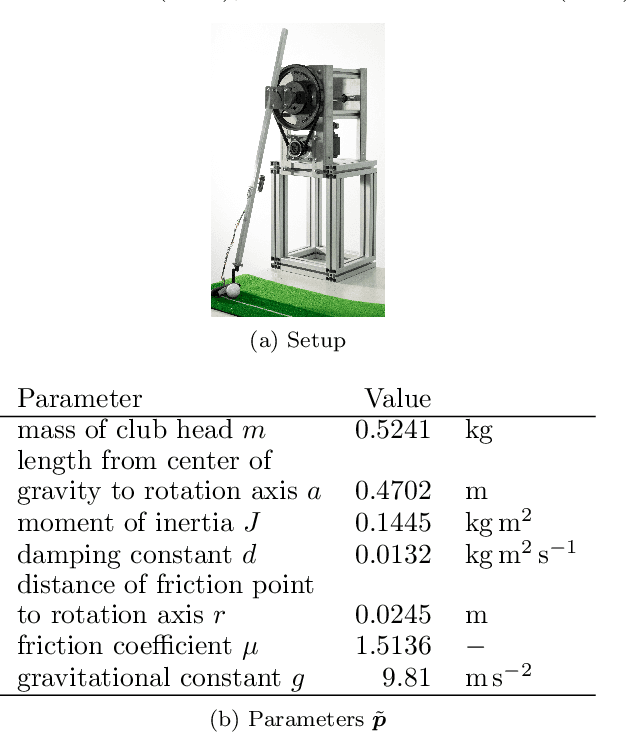
While trade-offs between modeling effort and model accuracy remain a major concern with system identification, resorting to data-driven methods often leads to a complete disregard for physical plausibility. To address this issue, we propose a physics-guided hybrid approach for modeling non-autonomous systems under control. Starting from a traditional physics-based model, this is extended by a recurrent neural network and trained using a sophisticated multi-objective strategy yielding physically plausible models. While purely data-driven methods fail to produce satisfying results, experiments conducted on real data reveal substantial accuracy improvements by our approach compared to a physics-based model.