Efficient Learning of Generalized Linear and Single Index Models with Isotonic Regression

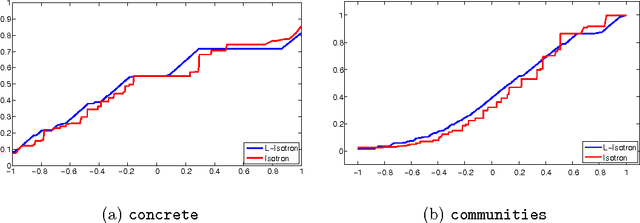
Generalized Linear Models (GLMs) and Single Index Models (SIMs) provide powerful generalizations of linear regression, where the target variable is assumed to be a (possibly unknown) 1-dimensional function of a linear predictor. In general, these problems entail non-convex estimation procedures, and, in practice, iterative local search heuristics are often used. Kalai and Sastry (2009) recently provided the first provably efficient method for learning SIMs and GLMs, under the assumptions that the data are in fact generated under a GLM and under certain monotonicity and Lipschitz constraints. However, to obtain provable performance, the method requires a fresh sample every iteration. In this paper, we provide algorithms for learning GLMs and SIMs, which are both computationally and statistically efficient. We also provide an empirical study, demonstrating their feasibility in practice.

Robust Distributed Online Prediction

The standard model of online prediction deals with serial processing of inputs by a single processor. However, in large-scale online prediction problems, where inputs arrive at a high rate, an increasingly common necessity is to distribute the computation across several processors. A non-trivial challenge is to design distributed algorithms for online prediction, which maintain good regret guarantees. In \cite{DMB}, we presented the DMB algorithm, which is a generic framework to convert any serial gradient-based online prediction algorithm into a distributed algorithm. Moreover, its regret guarantee is asymptotically optimal for smooth convex loss functions and stochastic inputs. On the flip side, it is fragile to many types of failures that are common in distributed environments. In this companion paper, we present variants of the DMB algorithm, which are resilient to many types of network failures, and tolerant to varying performance of the computing nodes.

Learning Kernel-Based Halfspaces with the Zero-One Loss

We describe and analyze a new algorithm for agnostically learning kernel-based halfspaces with respect to the \emph{zero-one} loss function. Unlike most previous formulations which rely on surrogate convex loss functions (e.g. hinge-loss in SVM and log-loss in logistic regression), we provide finite time/sample guarantees with respect to the more natural zero-one loss function. The proposed algorithm can learn kernel-based halfspaces in worst-case time $\poly(\exp(L\log(L/\epsilon)))$, for $\emph{any}$ distribution, where $L$ is a Lipschitz constant (which can be thought of as the reciprocal of the margin), and the learned classifier is worse than the optimal halfspace by at most $\epsilon$. We also prove a hardness result, showing that under a certain cryptographic assumption, no algorithm can learn kernel-based halfspaces in time polynomial in $L$.

Online Learning of Noisy Data with Kernels

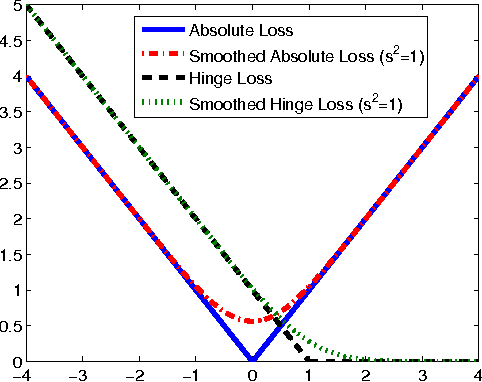
We study online learning when individual instances are corrupted by adversarially chosen random noise. We assume the noise distribution is unknown, and may change over time with no restriction other than having zero mean and bounded variance. Our technique relies on a family of unbiased estimators for non-linear functions, which may be of independent interest. We show that a variant of online gradient descent can learn functions in any dot-product (e.g., polynomial) or Gaussian kernel space with any analytic convex loss function. Our variant uses randomized estimates that need to query a random number of noisy copies of each instance, where with high probability this number is upper bounded by a constant. Allowing such multiple queries cannot be avoided: Indeed, we show that online learning is in general impossible when only one noisy copy of each instance can be accessed.

Efficient Learning with Partially Observed Attributes

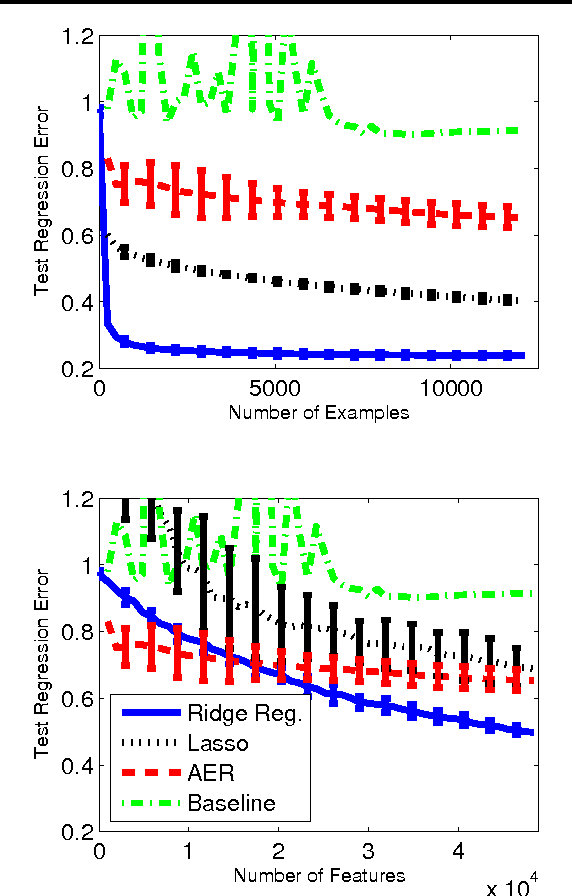
We describe and analyze efficient algorithms for learning a linear predictor from examples when the learner can only view a few attributes of each training example. This is the case, for instance, in medical research, where each patient participating in the experiment is only willing to go through a small number of tests. Our analysis bounds the number of additional examples sufficient to compensate for the lack of full information on each training example. We demonstrate the efficiency of our algorithms by showing that when running on digit recognition data, they obtain a high prediction accuracy even when the learner gets to see only four pixels of each image.