Speeding up SOR Solvers for Constraint-based GUIs with a Warm-Start Strategy

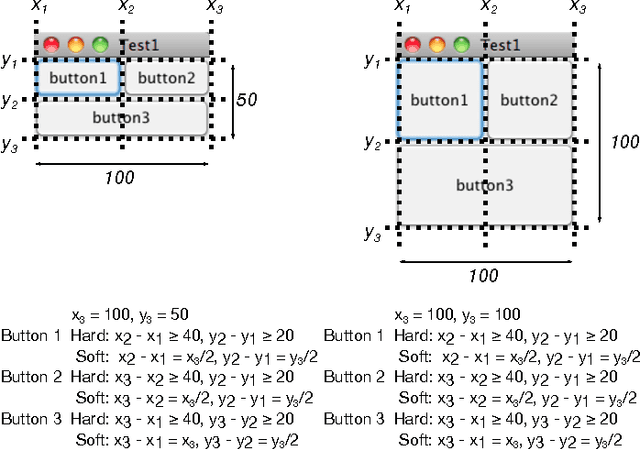
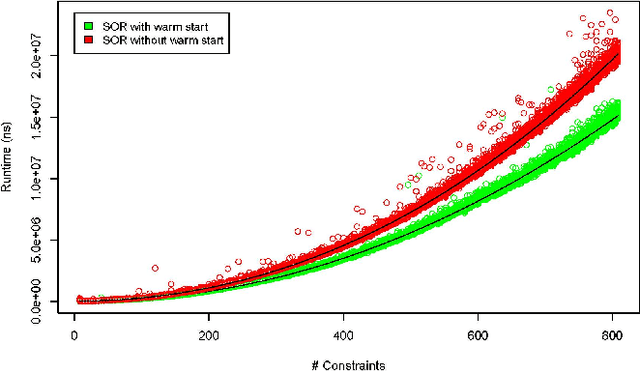
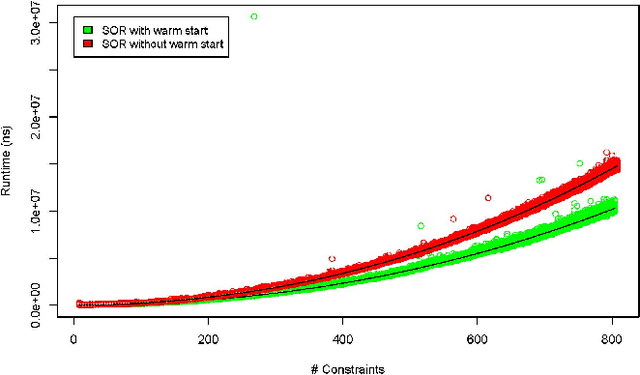
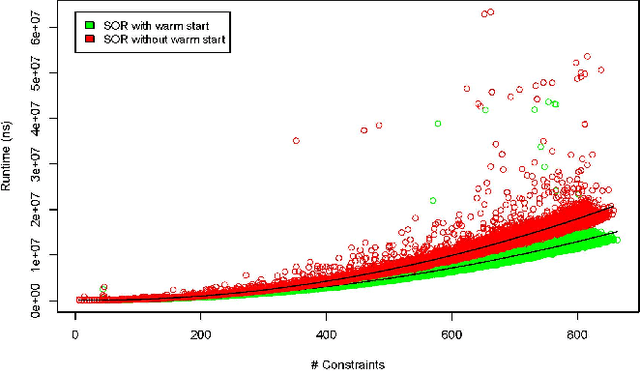
Many computer programs have graphical user interfaces (GUIs), which need good layout to make efficient use of the available screen real estate. Most GUIs do not have a fixed layout, but are resizable and able to adapt themselves. Constraints are a powerful tool for specifying adaptable GUI layouts: they are used to specify a layout in a general form, and a constraint solver is used to find a satisfying concrete layout, e.g.\ for a specific GUI size. The constraint solver has to calculate a new layout every time a GUI is resized or changed, so it needs to be efficient to ensure a good user experience. One approach for constraint solvers is based on the Gauss-Seidel algorithm and successive over-relaxation (SOR). Our observation is that a solution after resizing or changing is similar in structure to a previous solution. Thus, our hypothesis is that we can increase the computational performance of an SOR-based constraint solver if we reuse the solution of a previous layout to warm-start the solving of a new layout. In this paper we report on experiments to test this hypothesis experimentally for three common use cases: big-step resizing, small-step resizing and constraint change. In our experiments, we measured the solving time for randomly generated GUI layout specifications of various sizes. For all three cases we found that the performance is improved if an existing solution is used as a starting solution for a new layout.

Constraint Solvers for User Interface Layout

Constraints have played an important role in the construction of GUIs, where they are mainly used to define the layout of the widgets. Resizing behavior is very important in GUIs because areas have domain specific parameters such as form the resizing of windows. If linear objective function is used and window is resized then error is not distributed equally. To distribute the error equally, a quadratic objective function is introduced. Different algorithms are widely used for solving linear constraints and quadratic problems in a variety of different scientific areas. The linear relxation, Kaczmarz, direct and linear programming methods are common methods for solving linear constraints for GUI layout. The interior point and active set methods are most commonly used techniques to solve quadratic programming problems. Current constraint solvers designed for GUI layout do not use interior point methods for solving a quadratic objective function subject to linear equality and inequality constraints. In this paper, performance aspects and the convergence speed of interior point and active set methods are compared along with one most commonly used linear programming method when they are implemented for graphical user interface layout. The performance and convergence of the proposed algorithms are evaluated empirically using randomly generated UI layout specifications of various sizes. The results show that the interior point algorithms perform significantly better than the Simplex method and QOCA-solver, which uses the active set method implementation for solving quadratic optimization.