Lag Operator SSMs: A Geometric Framework for Structured State Space Modeling

Structured State Space Models (SSMs), which are at the heart of the recently popular Mamba architecture, are powerful tools for sequence modeling. However, their theoretical foundation relies on a complex, multi-stage process of continuous-time modeling and subsequent discretization, which can obscure intuition. We introduce a direct, first-principles framework for constructing discrete-time SSMs that is both flexible and modular. Our approach is based on a novel lag operator, which geometrically derives the discrete-time recurrence by measuring how the system's basis functions "slide" and change from one timestep to the next. The resulting state matrices are computed via a single inner product involving this operator, offering a modular design space for creating novel SSMs by flexibly combining different basis functions and time-warping schemes. To validate our approach, we demonstrate that a specific instance exactly recovers the recurrence of the influential HiPPO model. Numerical simulations confirm our derivation, providing new theoretical tools for designing flexible and robust sequence models.

Geometry of EM and related iterative algorithms

The Expectation--Maximization (EM) algorithm is a simple meta-algorithm that has been used for many years as a methodology for statistical inference when there are missing measurements in the observed data or when the data is composed of observables and unobservables. Its general properties are well studied, and also, there are countless ways to apply it to individual problems. In this paper, we introduce the $em$ algorithm, an information geometric formulation of the EM algorithm, and its extensions and applications to various problems. Specifically, we will see that it is possible to formulate an outlier-robust inference algorithm, an algorithm for calculating channel capacity, parameter estimation methods on probability simplex, particular multivariate analysis methods such as principal component analysis in a space of probability models and modal regression, matrix factorization, and learning generative models, which have recently attracted attention in deep learning, from the geometric perspective.

Fast and robust multiplane single molecule localization microscopy using deep neural network

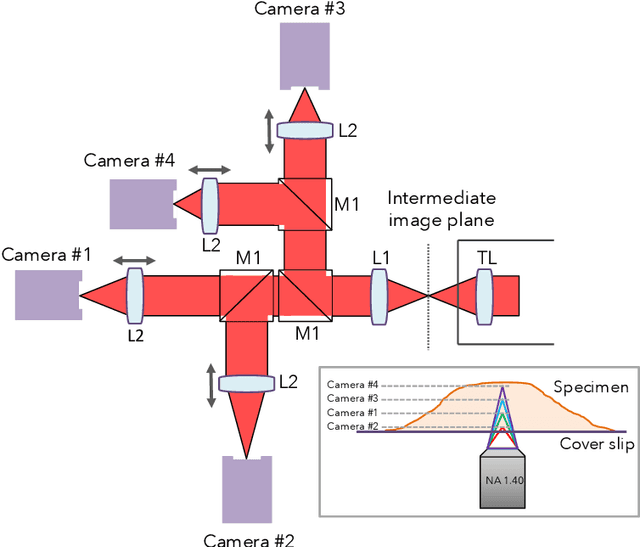
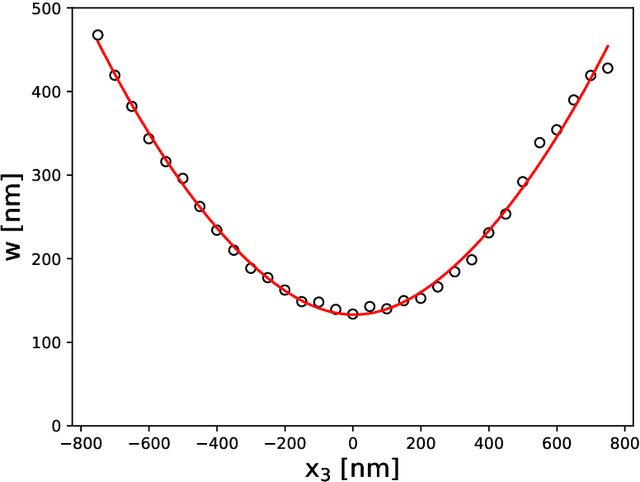
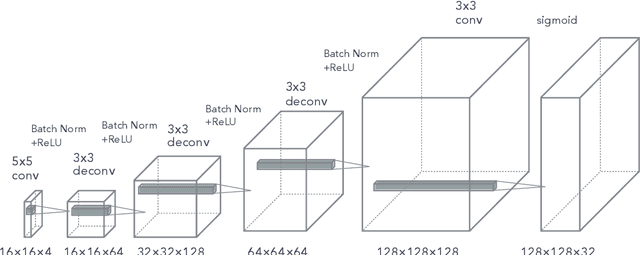
Single molecule localization microscopy is widely used in biological research for measuring the nanostructures of samples smaller than the diffraction limit. This study uses multifocal plane microscopy and addresses the 3D single molecule localization problem, where lateral and axial locations of molecules are estimated. However, when we multifocal plane microscopy is used, the estimation accuracy of 3D localization is easily deteriorated by the small lateral drifts of camera positions. We formulate a 3D molecule localization problem along with the estimation of the lateral drifts as a compressed sensing problem, A deep neural network was applied to accurately and efficiently solve this problem. The proposed method is robust to the lateral drifts and achieves an accuracy of 20 nm laterally and 50 nm axially without an explicit drift correction.

On a convergence property of a geometrical algorithm for statistical manifolds

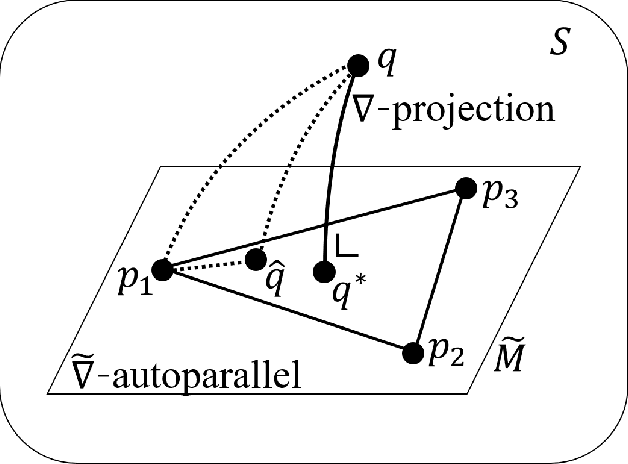
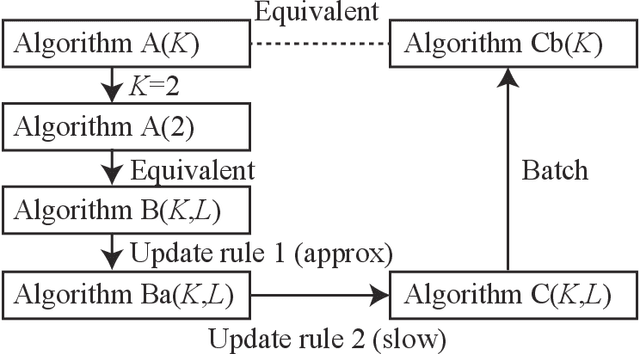
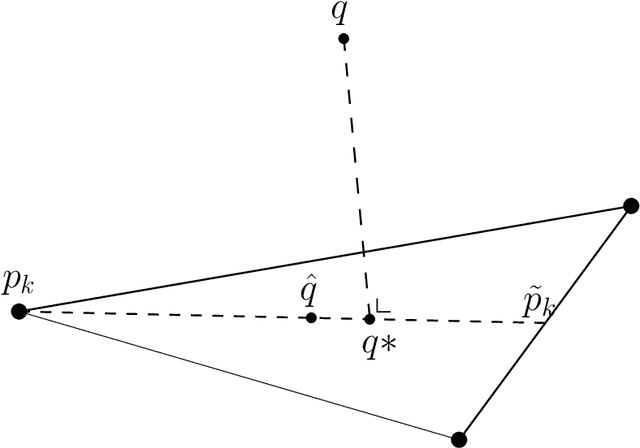
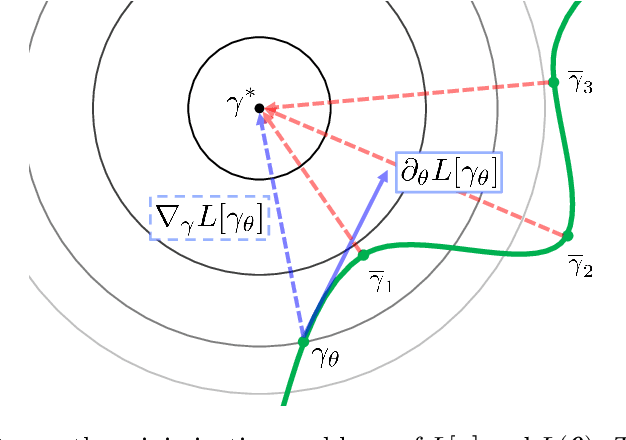
In this paper, we examine a geometrical projection algorithm for statistical inference. The algorithm is based on Pythagorean relation and it is derivative-free as well as representation-free that is useful in nonparametric cases. We derive a bound of learning rate to guarantee local convergence. In special cases of m-mixture and e-mixture estimation problems, we calculate specific forms of the bound that can be used easily in practice.

Transport Analysis of Infinitely Deep Neural Network

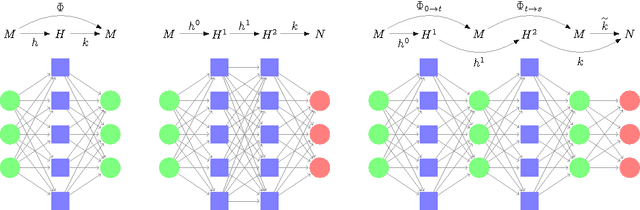
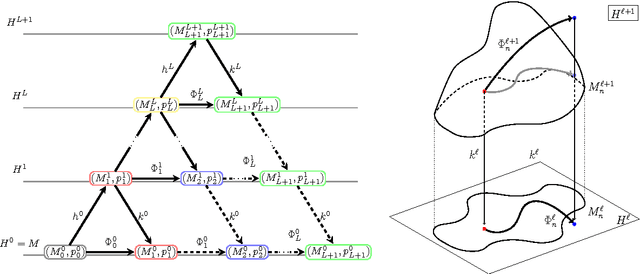
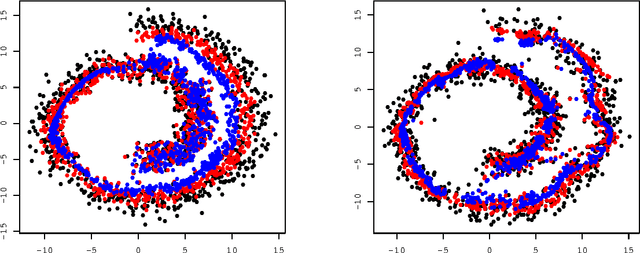
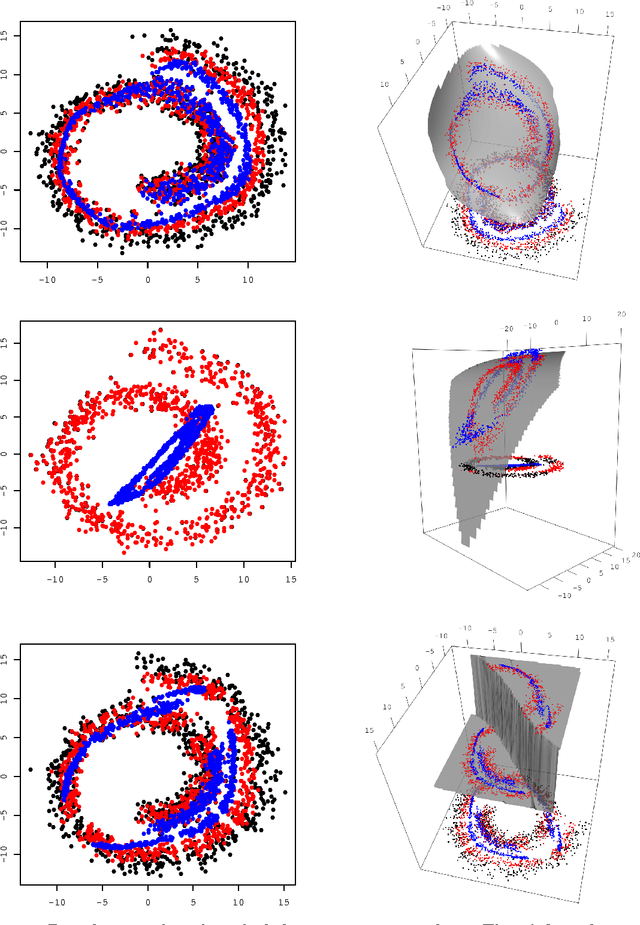
We investigated the feature map inside deep neural networks (DNNs) by tracking the transport map. We are interested in the role of depth (why do DNNs perform better than shallow models?) and the interpretation of DNNs (what do intermediate layers do?) Despite the rapid development in their application, DNNs remain analytically unexplained because the hidden layers are nested and the parameters are not faithful. Inspired by the integral representation of shallow NNs, which is the continuum limit of the width, or the hidden unit number, we developed the flow representation and transport analysis of DNNs. The flow representation is the continuum limit of the depth or the hidden layer number, and it is specified by an ordinary differential equation with a vector field. We interpret an ordinary DNN as a transport map or a Euler broken line approximation of the flow. Technically speaking, a dynamical system is a natural model for the nested feature maps. In addition, it opens a new way to the coordinate-free treatment of DNNs by avoiding the redundant parametrization of DNNs. Following Wasserstein geometry, we analyze a flow in three aspects: dynamical system, continuity equation, and Wasserstein gradient flow. A key finding is that we specified a series of transport maps of the denoising autoencoder (DAE). Starting from the shallow DAE, this paper develops three topics: the transport map of the deep DAE, the equivalence between the stacked DAE and the composition of DAEs, and the development of the double continuum limit or the integral representation of the flow representation. As partial answers to the research questions, we found that deeper DAEs converge faster and the extracted features are better; in addition, a deep Gaussian DAE transports mass to decrease the Shannon entropy of the data distribution.

Integral representation of shallow neural network that attains the global minimum

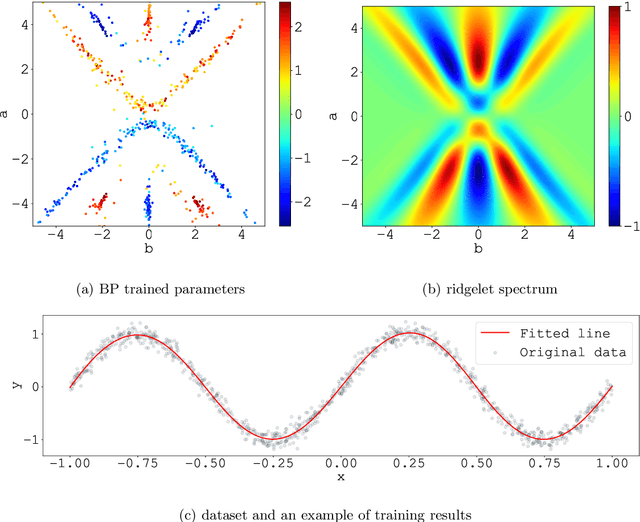
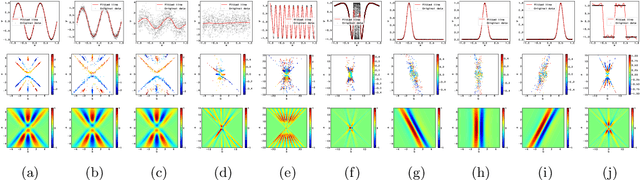
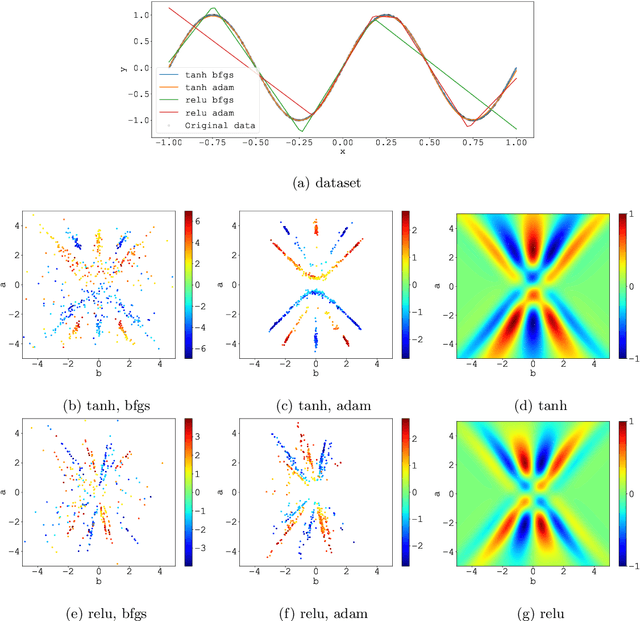
We consider the supervised learning problem with shallow neural networks. According to our unpublished experiments conducted several years prior to this study, we had noticed an interesting similarity between the distribution of hidden parameters after backprobagation (BP) training, and the ridgelet spectrum of the same dataset. Therefore, we conjectured that the distribution is expressed as a version of ridgelet transform, but it was not proven until this study. One difficulty is that both the local minimizers and the ridgelet transforms have an infinite number of varieties, and no relations are known between them. By using the integral representation, we reformulate the BP training as a strong-convex optimization problem and find a global minimizer. Finally, by developing ridgelet analysis on a reproducing kernel Hilbert space (RKHS), we write the minimizer explicitly and succeed to prove the conjecture. The modified ridgelet transform has an explicit expression that can be computed by numerical integration, which suggests that we can obtain the global minimizer of BP, without BP.

Transportation analysis of denoising autoencoders: a novel method for analyzing deep neural networks

The feature map obtained from the denoising autoencoder (DAE) is investigated by determining transportation dynamics of the DAE, which is a cornerstone for deep learning. Despite the rapid development in its application, deep neural networks remain analytically unexplained, because the feature maps are nested and parameters are not faithful. In this paper, we address the problem of the formulation of nested complex of parameters by regarding the feature map as a transport map. Even when a feature map has different dimensions between input and output, we can regard it as a transportation map by considering that both the input and output spaces are embedded in a common high-dimensional space. In addition, the trajectory is a geometric object and thus, is independent of parameterization. In this manner, transportation can be regarded as a universal character of deep neural networks. By determining and analyzing the transportation dynamics, we can understand the behavior of a deep neural network. In this paper, we investigate a fundamental case of deep neural networks: the DAE. We derive the transport map of the DAE, and reveal that the infinitely deep DAE transports mass to decrease a certain quantity, such as entropy, of the data distribution. These results though analytically simple, shed light on the correspondence between deep neural networks and the Wasserstein gradient flows.

Double Sparse Multi-Frame Image Super Resolution

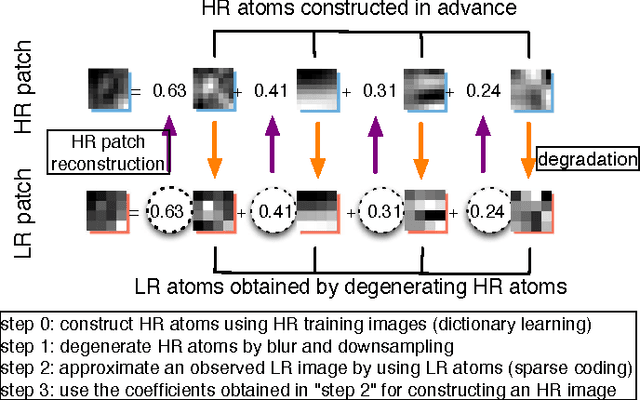
A large number of image super resolution algorithms based on the sparse coding are proposed, and some algorithms realize the multi-frame super resolution. In multi-frame super resolution based on the sparse coding, both accurate image registration and sparse coding are required. Previous study on multi-frame super resolution based on sparse coding firstly apply block matching for image registration, followed by sparse coding to enhance the image resolution. In this paper, these two problems are solved by optimizing a single objective function. The results of numerical experiments support the effectiveness of the proposed approch.

Neural Network with Unbounded Activation Functions is Universal Approximator

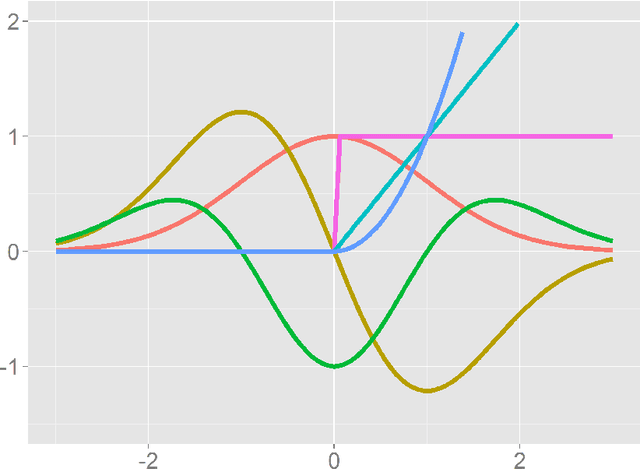
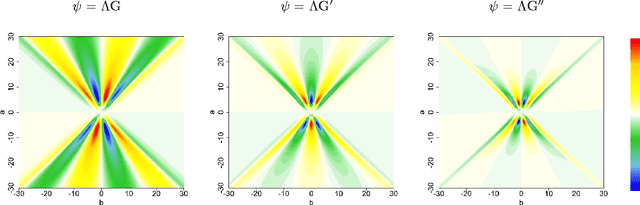
This paper presents an investigation of the approximation property of neural networks with unbounded activation functions, such as the rectified linear unit (ReLU), which is the new de-facto standard of deep learning. The ReLU network can be analyzed by the ridgelet transform with respect to Lizorkin distributions. By showing three reconstruction formulas by using the Fourier slice theorem, the Radon transform, and Parseval's relation, it is shown that a neural network with unbounded activation functions still satisfies the universal approximation property. As an additional consequence, the ridgelet transform, or the backprojection filter in the Radon domain, is what the network learns after backpropagation. Subject to a constructive admissibility condition, the trained network can be obtained by simply discretizing the ridgelet transform, without backpropagation. Numerical examples not only support the consistency of the admissibility condition but also imply that some non-admissible cases result in low-pass filtering.

Nonparametric Weight Initialization of Neural Networks via Integral Representation

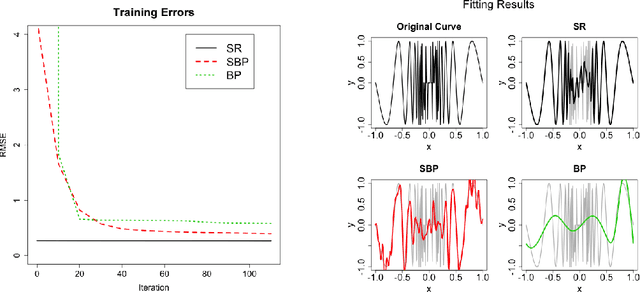
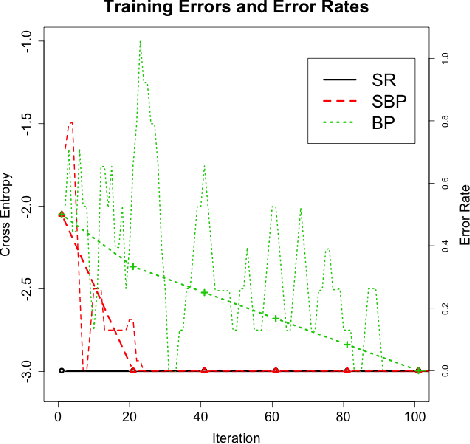
A new initialization method for hidden parameters in a neural network is proposed. Derived from the integral representation of the neural network, a nonparametric probability distribution of hidden parameters is introduced. In this proposal, hidden parameters are initialized by samples drawn from this distribution, and output parameters are fitted by ordinary linear regression. Numerical experiments show that backpropagation with proposed initialization converges faster than uniformly random initialization. Also it is shown that the proposed method achieves enough accuracy by itself without backpropagation in some cases.