Noam Wolf
Frank-Wolfe with a Nearest Extreme Point Oracle
Feb 03, 2021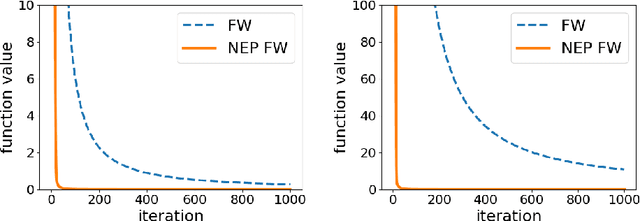
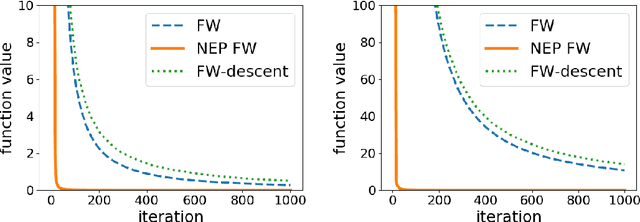
Abstract:We consider variants of the classical Frank-Wolfe algorithm for constrained smooth convex minimization, that instead of access to the standard oracle for minimizing a linear function over the feasible set, have access to an oracle that can find an extreme point of the feasible set that is closest in Euclidean distance to a given vector. We first show that for many feasible sets of interest, such an oracle can be implemented with the same complexity as the standard linear optimization oracle. We then show that with such an oracle we can design new Frank-Wolfe variants which enjoy significantly improved complexity bounds in case the set of optimal solutions lies in the convex hull of a subset of extreme points with small diameter (e.g., a low-dimensional face of a polytope). In particular, for many $0\text{--}1$ polytopes, under quadratic growth and strict complementarity conditions, we obtain the first linearly convergent variant with rate that depends only on the dimension of the optimal face and not on the ambient dimension.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge