Detect and Correct: A Selective Noise Correction Method for Learning with Noisy Labels

Falsely annotated samples, also known as noisy labels, can significantly harm the performance of deep learning models. Two main approaches for learning with noisy labels are global noise estimation and data filtering. Global noise estimation approximates the noise across the entire dataset using a noise transition matrix, but it can unnecessarily adjust correct labels, leaving room for local improvements. Data filtering, on the other hand, discards potentially noisy samples but risks losing valuable data. Our method identifies potentially noisy samples based on their loss distribution. We then apply a selection process to separate noisy and clean samples and learn a noise transition matrix to correct the loss for noisy samples while leaving the clean data unaffected, thereby improving the training process. Our approach ensures robust learning and enhanced model performance by preserving valuable information from noisy samples and refining the correction process. We applied our method to standard image datasets (MNIST, CIFAR-10, and CIFAR-100) and a biological scRNA-seq cell-type annotation dataset. We observed a significant improvement in model accuracy and robustness compared to traditional methods.

Inherent Inconsistencies of Feature Importance

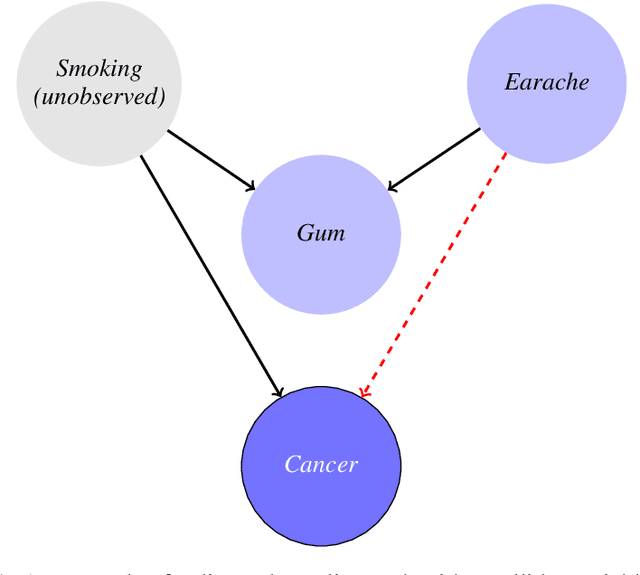
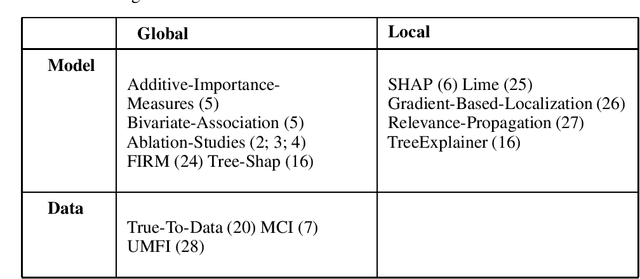
The black-box nature of modern machine learning techniques invokes a practical and ethical need for explainability. Feature importance aims to meet this need by assigning scores to features, so humans can understand their influence on predictions. Feature importance can be used to explain predictions under different settings: of the entire sample space or a specific instance; of model behavior, or the dependencies in the data themselves. However, in most cases thus far, each of these settings was studied in isolation. We attempt to develop a sound feature importance score framework by defining a small set of desired properties. Surprisingly, we prove an inconsistency theorem, showing that the expected properties cannot hold simultaneously. To overcome this difficulty, we propose the novel notion of re-partitioning the feature space into separable sets. Such sets are constructed to contain features that exhibit inter-set independence with respect to the target variable. We show that there exists a unique maximal partitioning into separable sets. Moreover, assigning scores to separable sets, instead of single features, unifies the results of commonly used feature importance scores and annihilates the inconsistencies we demonstrated.