Machine-Learned Phase Diagrams of Generalized Kitaev Honeycomb Magnets

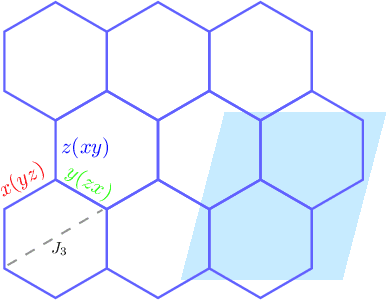
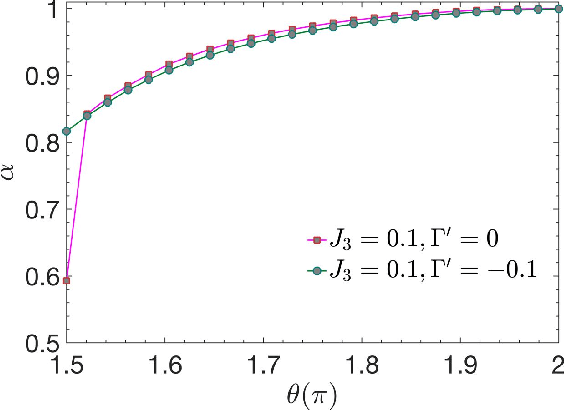
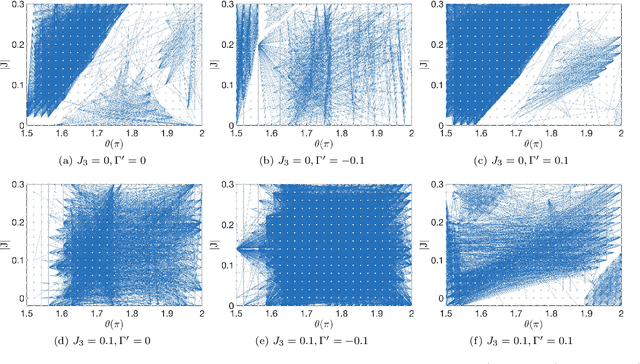
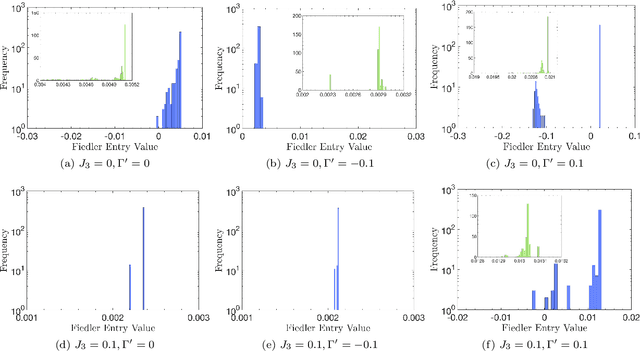
We use a recently developed interpretable and unsupervised machine-learning method, the tensorial kernel support vector machine (TK-SVM), to investigate the low-temperature classical phase diagram of a generalized Heisenberg-Kitaev-$\Gamma$ ($J$-$K$-$\Gamma$) model on a honeycomb lattice. Aside from reproducing phases reported by previous quantum and classical studies, our machine finds a hitherto missed nested zigzag-stripy order and establishes the robustness of a recently identified modulated $S_3 \times Z_3$ phase, which emerges through the competition between the Kitaev and $\Gamma$ spin liquids, against Heisenberg interactions. The results imply that, in the restricted parameter space spanned by the three primary exchange interactions -- $J$, $K$, and $\Gamma$, the representative Kitaev material $\alpha$-${\rm RuCl}_3$ lies close to the interface of several phases, including a simple ferromagnet, and the unconventional $S_3 \times Z_3$ and nested zigzag-stripy magnets. A zigzag order is stabilized by a finite $\Gamma^{\prime}$ and/or $J_3$ term, whereas the four magnetic orders may compete in particular if $\Gamma^{\prime}$ is anti-ferromagnetic.

Revealing the Phase Diagram of Kitaev Materials by Machine Learning: Cooperation and Competition between Spin Liquids

Kitaev materials are promising materials for hosting quantum spin liquids and investigating the interplay of topological and symmetry-breaking phases. We use an unsupervised and interpretable machine-learning method, the tensorial-kernel support vector machine, to study the classical honeycomb Kitaev-$\Gamma$ model in a magnetic field. Our machine learns the global phase diagram and the associated analytical order parameters, including several distinct spin liquids, two exotic $S_3$ magnets, and two modulated $S_3 \times Z_3$ magnets. We find that the extension of Kitaev spin liquids and a field-induced suppression of magnetic order already occur in the large-$S$ limit, implying that critical parts of the physics of Kitaev materials can be understood at the classical level. Moreover, the two $S_3 \times Z_3$ orders are induced by competition between Kitaev and $\Gamma$ spin liquids and feature a previously unknown type of spin-lattice entangled modulation, which requires a matrix description instead of scalar phase factors. Our work provides the first instance of a machine detecting new phases and paves the way towards the development of automated tools to explore unsolved problems in many-body physics.