Learning Mathematical Rules with Large Language Models

In this paper, we study the ability of large language models to learn specific mathematical rules such as distributivity or simplifying equations. We present an empirical analysis of their ability to generalize these rules, as well as to reuse them in the context of word problems. For this purpose, we provide a rigorous methodology to build synthetic data incorporating such rules, and perform fine-tuning of large language models on such data. Our experiments show that our model can learn and generalize these rules to some extent, as well as suitably reuse them in the context of word problems.

Ordinal Potential-based Player Rating

A two-player symmetric zero-sum game is transitive if for any pure strategies $x$, $y$, $z$, if $x$ is better than $y$, and $y$ is better than $z$, then $x$ is better than $z$. It was recently observed that the Elo rating fails at preserving transitive relations among strategies and therefore cannot correctly extract the transitive component of a game. Our first contribution is to show that the Elo rating actually does preserve transitivity when computed in the right space. Precisely, using a suitable invertible mapping $\varphi$, we first apply $\varphi$ to the game, then compute Elo ratings, then go back to the original space by applying $\varphi^{-1}$. We provide a characterization of transitive games as a weak variant of ordinal potential games with additively separable potential functions. Leveraging this insight, we introduce the concept of transitivity order, the minimum number of invertible mappings required to transform the payoff of a transitive game into (differences of) its potential function. The transitivity order is a tool to classify transitive games, with Elo games being an example of transitive games of order one. Most real-world games have both transitive and non-transitive (cyclic) components, and we use our analysis of transitivity to extract the transitive (potential) component of an arbitrary game. We link transitivity to the known concept of sign-rank: transitive games have sign-rank two; arbitrary games may have higher sign-rank. Using a neural network-based architecture, we learn a decomposition of an arbitrary game into transitive and cyclic components that prioritises capturing the sign pattern of the game. In particular, a transitive game always has just one component in its decomposition, the potential component. We provide a comprehensive evaluation of our methodology using both toy examples and empirical data from real-world games.

Towards Multi-Agent Reinforcement Learning driven Over-The-Counter Market Simulations

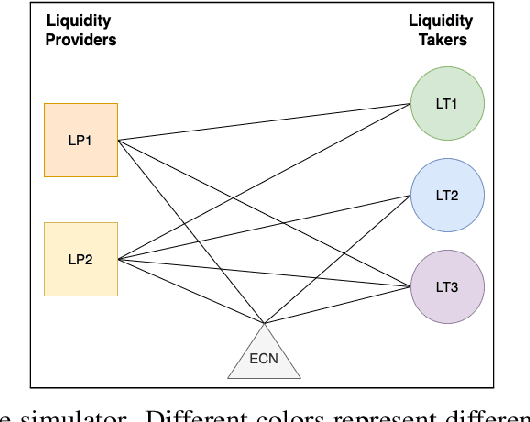
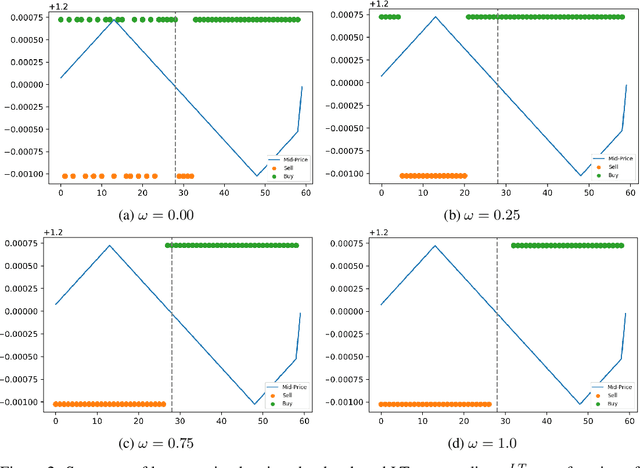
We study a game between liquidity provider and liquidity taker agents interacting in an over-the-counter market, for which the typical example is foreign exchange. We show how a suitable design of parameterized families of reward functions coupled with associated shared policy learning constitutes an efficient solution to this problem. Precisely, we show that our deep-reinforcement-learning-driven agents learn emergent behaviors relative to a wide spectrum of incentives encompassing profit-and-loss, optimal execution and market share, by playing against each other. In particular, we find that liquidity providers naturally learn to balance hedging and skewing as a function of their incentives, where the latter refers to setting their buy and sell prices asymmetrically as a function of their inventory. We further introduce a novel RL-based calibration algorithm which we found performed well at imposing constraints on the game equilibrium, both on toy and real market data.

Calibration of Derivative Pricing Models: a Multi-Agent Reinforcement Learning Perspective

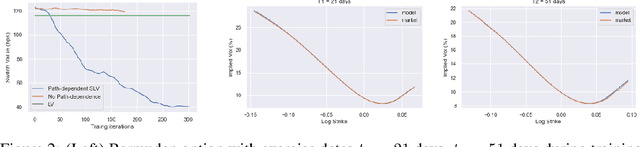
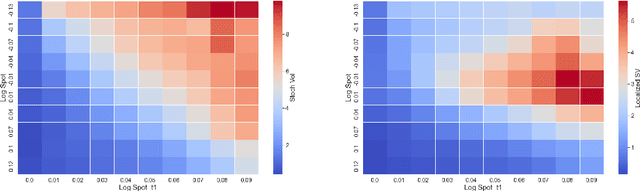
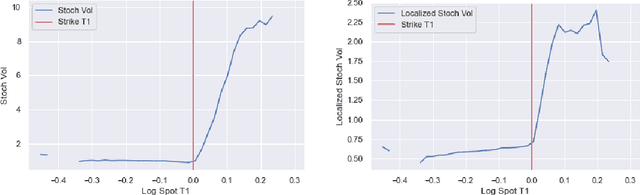
One of the most fundamental questions in quantitative finance is the existence of continuous-time diffusion models that fit market prices of a given set of options. Traditionally, one employs a mix of intuition, theoretical and empirical analysis to find models that achieve exact or approximate fits. Our contribution is to show how a suitable game theoretical formulation of this problem can help solve this question by leveraging existing developments in modern deep multi-agent reinforcement learning to search in the space of stochastic processes. More importantly, we hope that our techniques can be leveraged and extended by the community to solve important problems in that field, such as the joint SPX-VIX calibration problem. Our experiments show that we are able to learn local volatility, as well as path-dependence required in the volatility process to minimize the price of a Bermudan option. In one sentence, our algorithm can be seen as a particle method \`{a} la Guyon et Henry-Labordere where particles, instead of being designed to ensure $\sigma_{loc}(t,S_t)^2 = \mathbb{E}[\sigma_t^2|S_t]$, are learning RL-driven agents cooperating towards more general calibration targets. This is the first work bridging reinforcement learning with the derivative calibration problem.

Towards a fully RL-based Market Simulator

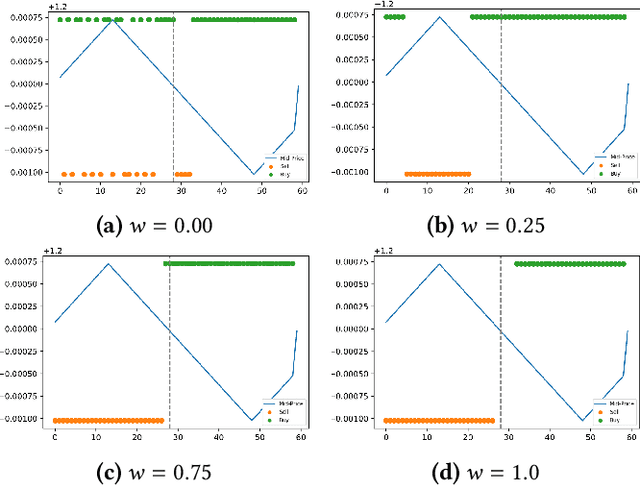
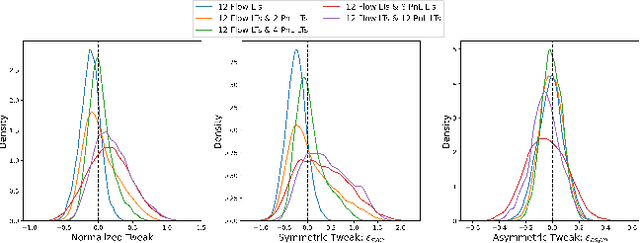
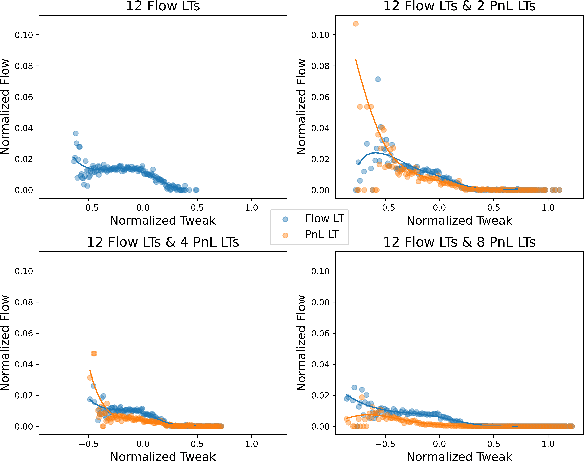
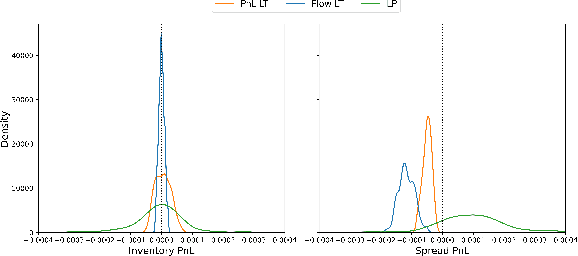
We present a new financial framework where two families of RL-based agents representing the Liquidity Providers and Liquidity Takers learn simultaneously to satisfy their objective. Thanks to a parametrized reward formulation and the use of Deep RL, each group learns a shared policy able to generalize and interpolate over a wide range of behaviors. This is a step towards a fully RL-based market simulator replicating complex market conditions particularly suited to study the dynamics of the financial market under various scenarios.

Consensus Multiplicative Weights Update: Learning to Learn using Projector-based Game Signatures

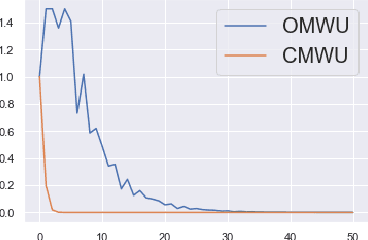
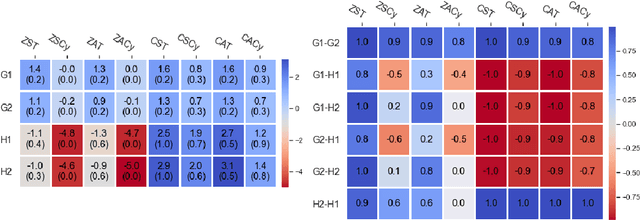
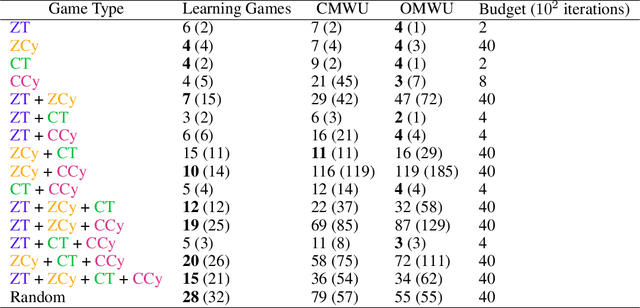
Recently, Optimistic Multiplicative Weights Update (OMWU) was proven to be the first constant step-size algorithm in the online no-regret framework to enjoy last-iterate convergence to Nash Equilibria in the constrained zero-sum bimatrix case, where weights represent the probabilities of playing pure strategies. We introduce the second such algorithm, \textit{Consensus MWU}, for which we prove local convergence and show empirically that it enjoys faster and more robust convergence than OMWU. Our algorithm shows the importance of a new object, the \textit{simplex Hessian}, as well as of the interaction of the game with the (eigen)space of vectors summing to zero, which we believe future research can build on. As for OMWU, CMWU has convergence guarantees in the zero-sum case only, but Cheung and Piliouras (2020) recently showed that OMWU and MWU display opposite convergence properties depending on whether the game is zero-sum or cooperative. Inspired by this work and the recent literature on learning to optimize for single functions, we extend CMWU to non zero-sum games by introducing a new framework for online learning in games, where the update rule's gradient and Hessian coefficients along a trajectory are learnt by a reinforcement learning policy that is conditioned on the nature of the game: \textit{the game signature}. We construct the latter using a new canonical decomposition of two-player games into eight components corresponding to commutative projection operators, generalizing and unifying recent game concepts studied in the literature. We show empirically that our new learning policy is able to exploit the game signature across a wide range of game types.

Causal Policy Gradients

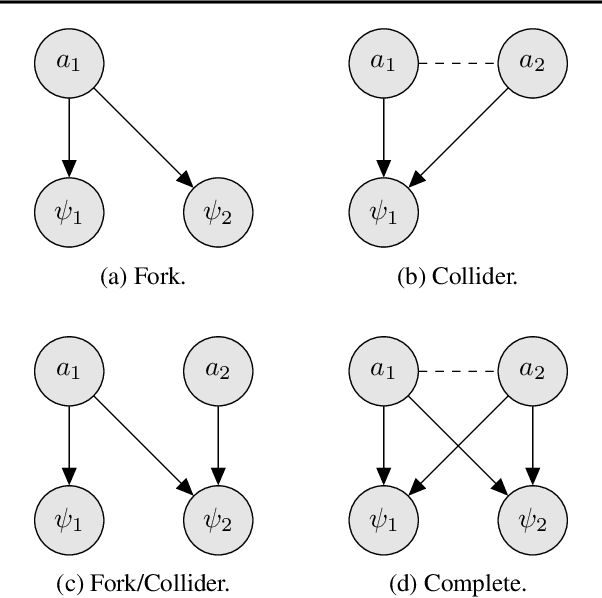
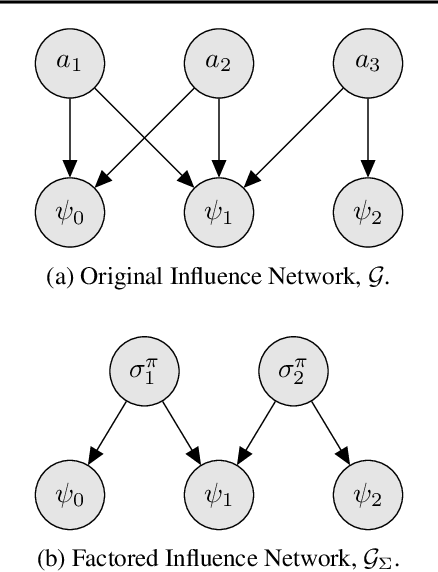
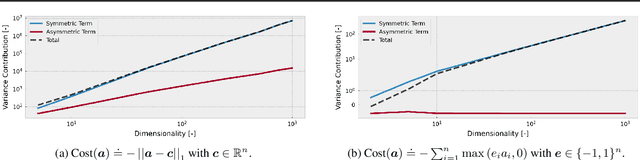
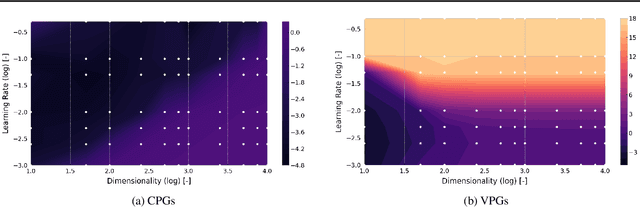
Policy gradient methods can solve complex tasks but often fail when the dimensionality of the action-space or objective multiplicity grow very large. This occurs, in part, because the variance on score-based gradient estimators scales quadratically with the number of targets. In this paper, we propose a causal baseline which exploits independence structure encoded in a novel action-target influence network. Causal policy gradients (CPGs), which follow, provide a common framework for analysing key state-of-the-art algorithms, are shown to generalise traditional policy gradients, and yield a principled way of incorporating prior knowledge of a problem domain's generative processes. We provide an analysis of the proposed estimator and identify the conditions under which variance is guaranteed to improve. The algorithmic aspects of CPGs are also discussed, including optimal policy factorisations, their complexity, and the use of conditioning to efficiently scale to extremely large, concurrent tasks. The performance advantages for two variants of the algorithm are demonstrated on large-scale bandit and concurrent inventory management problems.

Calibration of Shared Equilibria in General Sum Partially Observable Markov Games

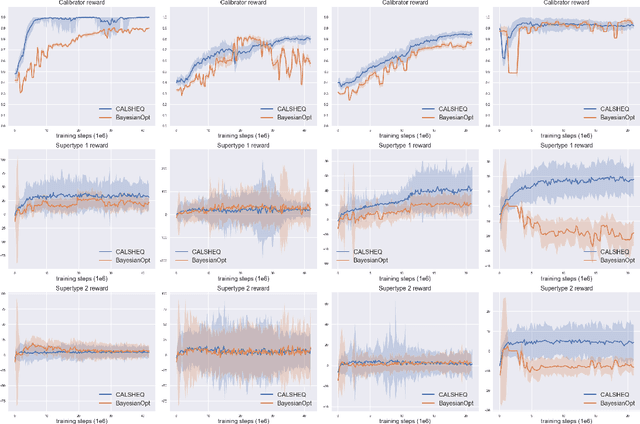
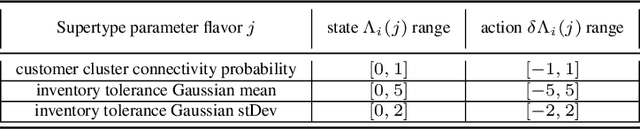
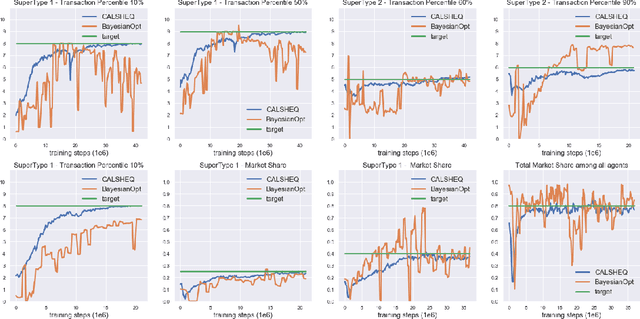
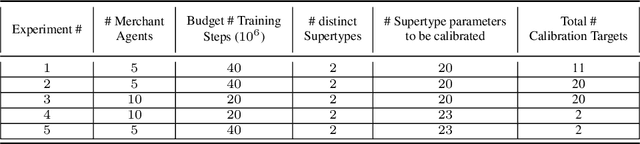
Training multi-agent systems (MAS) to achieve realistic equilibria gives us a useful tool to understand and model real-world systems. We consider a general sum partially observable Markov game where agents of different types share a single policy network, conditioned on agent-specific information. This paper aims at i) formally understanding equilibria reached by such agents, and ii) matching emergent phenomena of such equilibria to real-world targets. Parameter sharing with decentralized execution has been introduced as an efficient way to train multiple agents using a single policy network. However, the nature of resulting equilibria reached by such agents is not yet understood: we introduce the novel concept of \textit{Shared equilibrium} as a symmetric pure Nash equilibrium of a certain Functional Form Game (FFG) and prove convergence to the latter for a certain class of games using self-play. In addition, it is important that such equilibria satisfy certain constraints so that MAS are \textit{calibrated} to real world data for practical use: we solve this problem by introducing a novel dual-Reinforcement Learning based approach that fits emergent behaviors of agents in a Shared equilibrium to externally-specified targets, and apply our methods to a $n$-player market example. We do so by calibrating parameters governing distributions of agent types rather than individual agents, which allows both behavior differentiation among agents and coherent scaling of the shared policy network to multiple agents.

Risk-Sensitive Reinforcement Learning: a Martingale Approach to Reward Uncertainty

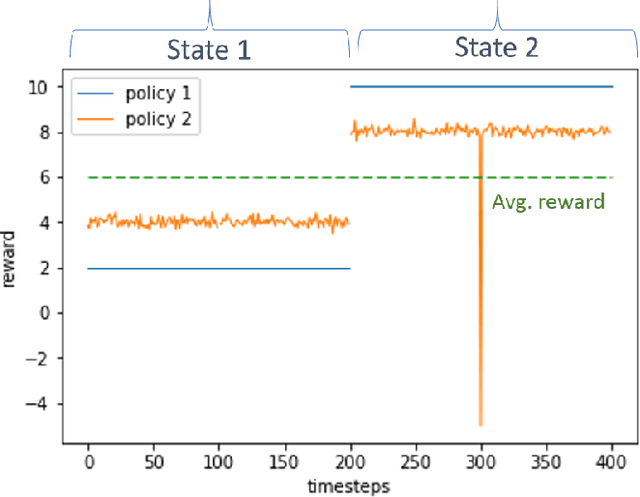
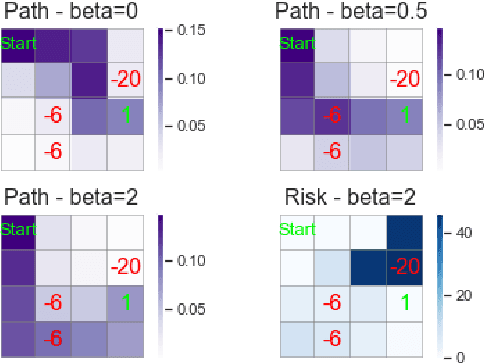
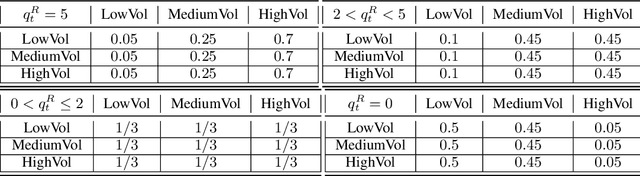
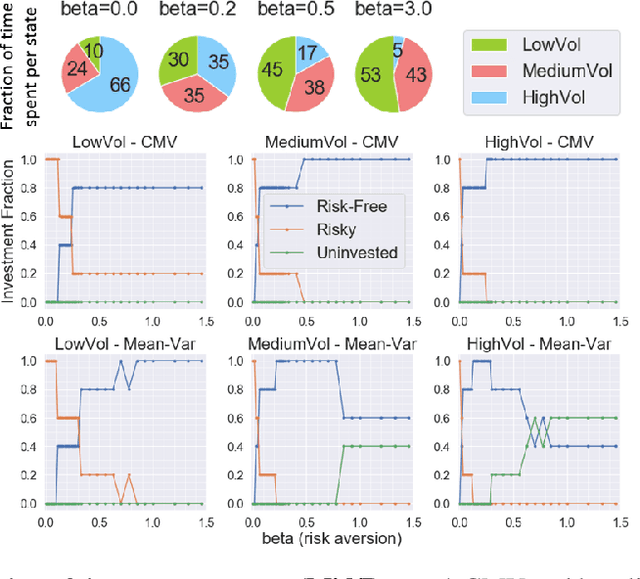
We introduce a novel framework to account for sensitivity to rewards uncertainty in sequential decision-making problems. While risk-sensitive formulations for Markov decision processes studied so far focus on the distribution of the cumulative reward as a whole, we aim at learning policies sensitive to the uncertain/stochastic nature of the rewards, which has the advantage of being conceptually more meaningful in some cases. To this end, we present a new decomposition of the randomness contained in the cumulative reward based on the Doob decomposition of a stochastic process, and introduce a new conceptual tool - the \textit{chaotic variation} - which can rigorously be interpreted as the risk measure of the martingale component associated to the cumulative reward process. We innovate on the reinforcement learning side by incorporating this new risk-sensitive approach into model-free algorithms, both policy gradient and value function based, and illustrate its relevance on grid world and portfolio optimization problems.

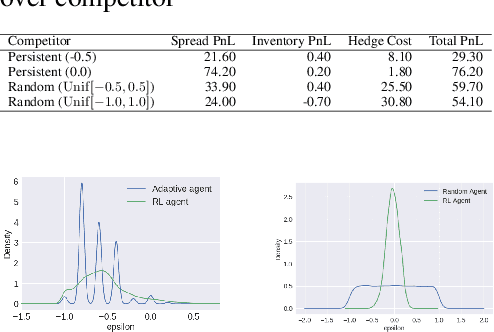
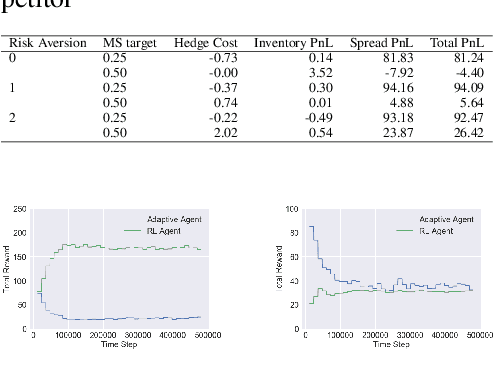
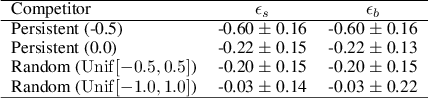
Reinforcement Learning for Market Making in a Multi-agent Dealer Market

Market makers play an important role in providing liquidity to markets by continuously quoting prices at which they are willing to buy and sell, and managing inventory risk. In this paper, we build a multi-agent simulation of a dealer market and demonstrate that it can be used to understand the behavior of a reinforcement learning (RL) based market maker agent. We use the simulator to train an RL-based market maker agent with different competitive scenarios, reward formulations and market price trends (drifts). We show that the reinforcement learning agent is able to learn about its competitor's pricing policy; it also learns to manage inventory by smartly selecting asymmetric prices on the buy and sell sides (skewing), and maintaining a positive (or negative) inventory depending on whether the market price drift is positive (or negative). Finally, we propose and test reward formulations for creating risk averse RL-based market maker agents.